Виды определителей и правила их вычисления.

Каждой квадратной матрице можно по определенным правилам поставить в соответствие некоторое число, которое называется ее определителем.

Определителем первого порядка называется число, соответствующее квадратной матрице 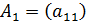, которое равно самому элементу .

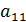Определителем второго порядка называется число, соответствующее квадратной матрице 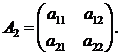, которое вычисляется по правилу: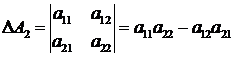

Пример.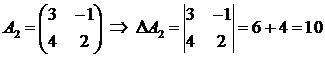

Определителем третьего порядка называется число, соответствующее квадратной матрице 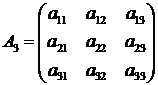, которое вычисляется по правилу:

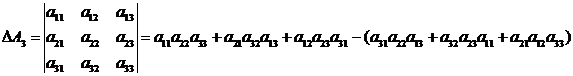
Это правило вычисления определителя третьего порядка называется правилом треугольников.

Пример.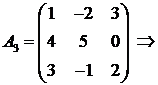

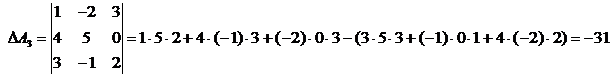
Определитель n-гопорядка можно разложить по элементам любой строки (любого столбца): 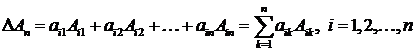- разложение определителя по элементам 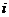-й строки.

или 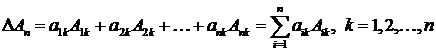- разложение определителя по элементам 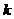-го столбца.

Замечание. Определитель треугольной матрицы равен произведению элементов главной диагонали.

Минор, алгебраическое дополнение.

Определение. Минором 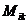элемента 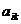квадратной матрицы 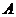называется определитель матрицы, получаемой из 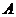вычеркиванием 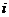-ой строки и 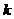-го столбца.

Пример.

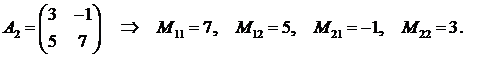
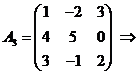
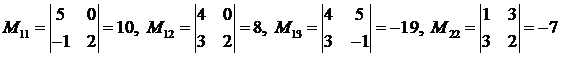
и так далее: матрица третьего порядка имеет 9 миноров.

Определение.Алгебраическим дополнением элемента 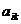квадратной матрицы 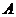называется число .

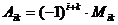Пример.

Для матрицы :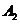

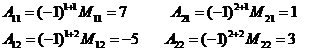
Для матрицы 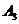: и так далее.

Определение.Определителем квадратной матрицы 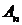порядка 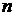называется число, которое записывается и вычисляется следующим образом:

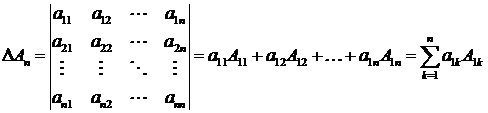
Это равенство называется разложением определителя по элементам первойстроки.

Пример.

Лекция № 2.

Тема: Решение систем линейных уравнений

План:

1. Формулы Крамера.

2. Метод обратной матрицы.

3. Метод Гаусса.

Формулы Крамера.

Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений.

Теорема. Система из n уравнений с n неизвестными

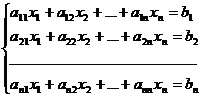
в случае, если определитель матрицы системы не равен нулю, то система имеет единственное решение и это решение находится по формулам: x_i = 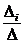где D = detA, а D_i – определитель матрицы, получаемой из матрицы системы заменой столбцаi столбцом свободных членов b_i.

D_i =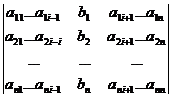

Пример. Найти решение системы уравнений: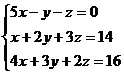

D = 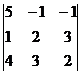= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;

D₁ = 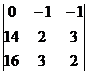= (28 – 48) – (42 – 32) = -20 – 10 = -30.

x₁ =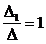

D₂ = 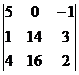= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.

x₂ =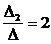

D₃ = 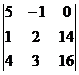= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.

x₃ =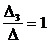

Замечание 1. Если система однородна, т.е. b_i = 0, то при D¹0 система имеет единственное нулевое решение x₁ = x₂ = … = x_n = 0.

Замечание 2. При D = 0 система имеет бесконечное множество решений.

Метод обратной матрицы.

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Пусть дана система уравнений: 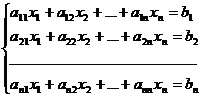Составим матрицы:

A = 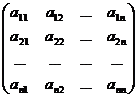- матрица коэффициентов при переменных или матрица системы;

B = - матрица –столбец свободных членов;

X = - матрица – столбец неизвестных.

Тогда систему уравнений можно записать:A×X = B.Домножим слева обе части равенства на A^-1: A^-1×A×X = A^-1×B, т.к. А^-1×А = Е, то Е×Х = А^-1×В, то справедлива следующая формула:

Х = А^-1×В

Таким образом, для применения данного метода необходимо находить обратную матрицу.

Пример. Решить систему уравнений: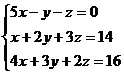

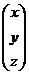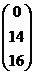Х = , B = , A =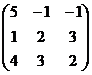

Найдем обратную матрицу А^-1.

D = detA = 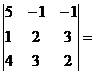5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30≠0 ⇒ обратная матрица существует.

M₁₁= 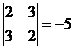; M₂₁ = 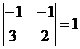; M₃₁ = ;

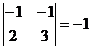M₁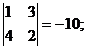₂ = M₂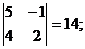₂ = M₃₂ =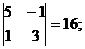

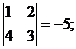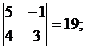M₁₃ = M₂₃ = M₃₃ =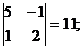

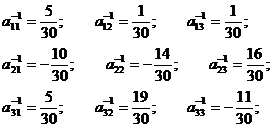
A^-1= ;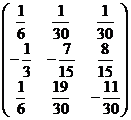

Cделаем проверку:

A×A^-1 = 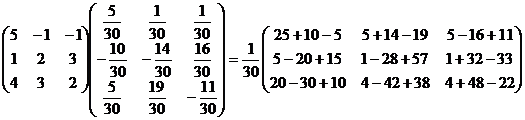=E.

Находим матрицу Х.

Х = 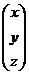= А^-1В = × = .

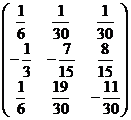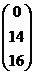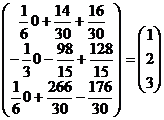Получили решения системы: x =1; y = 2; z = 3.

3.Метод Гаусса.

Пусть дана система m линейных уравнений с n неизвестными:

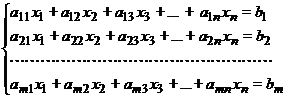
Полагая, что в системе коэффициент a₁₁ отличен от нуля (если это не так, то следует на первое место поставить уравнение с отличным от нуля коэффициентом при x₁). Преобразуем систему следующим образом: первое уравнение оставляем без изменения, а из всех остальных уравнений исключаем неизвестную x₁ с помощью эквивалентных преобразований описанным выше способом.

В полученной системе

,

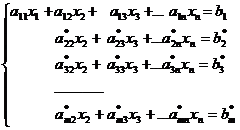считая, что 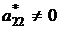(что всегда можно получить, переставив уравнения или слагаемые внутри уравнений), оставляем без изменений первые два уравнения системы, а из остальных уравнений, используя второе уравнения, с помощью элементарных преобразований исключаем неизвестную x₂. Во вновь полученной системе

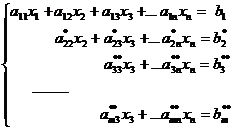
при условии 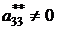оставляем без изменений первые три уравнения, а из всех остальных с помощью третьего уравнения элементарными преобразованиями исключаем неизвестную x₃.

Этот процесс продолжается до тех пор, пока не реализуется один из трех возможных случаев:

1)если в результате приходим к системе, одно из уравнений которой имеет нулевые коэффициенты при всех неизвестных и отличный от нуля свободный член, то исходная система несовместна;

2)если в результате преобразований получаем систему с матрицей коэффициентов треугольного вида, то система совместна и является определенной;

3)если получается ступенчатая система коэффициентов (и при этом не выполняется условие пункта 1), то система совместна и неопределенна.

Рассмотрим квадратную систему: 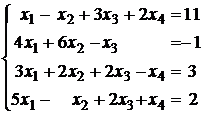(1)

У этой системы коэффициент a₁₁ отличен от нуля. Если бы это условие не выполнялось, то чтобы его получить, нужно было бы переставить местами уравнения, поставив первым то уравнение, у которого коэффициент при x₁ не равен нулю.

Проведем следующие преобразования системы:

1) поскольку a₁₁¹0, первое уравнение оставим без изменений;

2) вместо второго уравнения запишем уравнение, получающееся, если из второго уравнения вычесть первое, умноженное на 4;

3) вместо третьего уравнения запишем разность третьего и первого, умноженного на 3;

4) вместо четвертого уравнения запишем разность четвертого и первого, умноженного на 5.

Полученная новая система эквивалентна исходной и имеет во всех уравнениях, кроме первого, нулевые коэффициенты при x₁ (это и являлось целью преобразований 1 – 4): 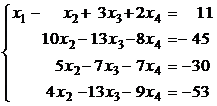(2)

Для приведенного преобразования и для всех дальнейших преобразований не следует целиком переписывать всю систему, как это только что сделано. Исходную систему можно представить в виде матрицы

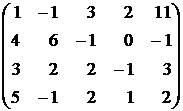. (3)

Матрица (3) называется расширенной матрицей для исходной системы уравнений. Если из расширенной матрицы удалить столбец свободных членов, то получится матрица коэффициентов системы, которую иногда называют просто матрицей системы.

Системе (2) соответствует расширенная матрица

.

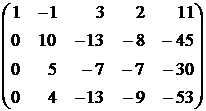Преобразуем эту матрицу следующим образом:

1) первые две строки оставим без изменения, поскольку элемент a₂₂ не равен нулю;

2) вместо третьей строки запишем разность между второй строкой и удвоенной третьей;

3) четвертую строку заменим разностью между удвоенной второй строкой и умноженной на 5 четвертой.

В результате получится матрица, соответствующая системе, у которой неизвестная x₁ исключена из всех уравнений, кроме первого, а неизвестная x₂ — из всех уравнений кроме первого и второго:

.

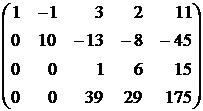Теперь исключим неизвестную x₃ из четвертого уравнения. Для этого последнюю матрицу преобразуем так:

1) первые три строки оставим без изменения, так как a₃₃¹ 0;

2) четвертую строку заменим разностью между третьей, умноженной на 39, и четвертой: .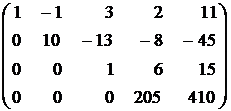

Полученная матрица соответствует системе

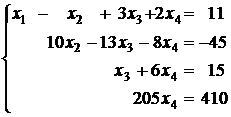. (4)

Из последнего уравнения этой системы получаем x₄ = 2. Подставив это значение в третье уравнение, получим x₃ = 3. Теперь из второго уравнения следует, что x₂ = 1, а из первого — x₁ = –1. Очевидно, что полученное решение единственно (так как единственным образом определяется значение x₄, затем x₃ и т. д.).

Определение: Назовем квадратную матрицу, у которой на главной диагонали стоят числа, отличные от нуля, а под главной диагональю – нули, треугольной матрицей.

Матрица коэффициентов системы (4) – треугольная матрица.