Воробьевой Ольги и Пырина Артема

ФО-310501

Нечеткое множество

Нечеткое множество Аопределяется как множество упорядоченных пар:

<x, µ_A (x)>

где хявляется элементом некоторого универсального множества или универсума X, а µ_A (x) — функция принадлежности, µ_A : X → [0,1]

Композиция нечетких отношений

Максминной композицией (произведением) нечетких отношений и , заданных на X × Z и Z × Y, называется нечеткое отношение = ◦ на X × Y с функцией принадлежности

µ_G~(x,y) = (µ_A~(x,z), µ_B~(z,y)),

(x,y) X × Y, (x,z) X × Z, (z,y) Z × Y.

В случае конечных множеств X,Y,Z матрица нечеткого отношения = ◦ рассчитывается как максминное произведение матриц и . Эта операция выполняется как обычное произведение матриц, в котором поэлементное умножение заменено операцией минимума, а суммирование – операцией максимума.

Операции над нечеткими множествами

· Дополнением нечеткого множества , заданного на U, называется нечеткое множество с функцией принадлежности µ_A-(u) = 1 - µ_A(u) для всех u U.

· Пересечением нечетких множеств и , заданных на U, называется нечеткое множество = с функцией принадлежности µ_C(u) = min (µ_A(u), µ_B(u)) для всех u U.

· Объединением нечетких множеств и , заданных на U, называется нечеткое множество D = с функцией принадлежности µ_D(u) = max (µ_A(u), µ_B(u)) для всех u U.

Задача обучения без учителя, таксономия

Дано конечное множество М векторов размерности n.

Требуется разбить множество М на непересекающиеся подмножества (кластеры, таксоны), причем объекты, входящие в один кластер (таксон), должны быть достаточно близки друг к другу с точки зрения выбранного критерия близости ( расстояния), а элементы из разных кластеров (таксонов) должны быть достаточно далеки друг от друга.

Образ в ТА - таксон – множество объектов x, y, таких, что | x-y| < ρ

Постановка задачи поиска информативного пространства

Задача поиска информативных подсистем признаковсостоит в нахождении системы признаков (подпространства), в которой задача ДА решается достаточно качественно (с точки зрения того или иного критерия ).

2.2.

2.3.

Ключевые понятия теории нечетких множеств

Композиция нечетких отношений

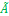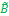Максминной композицией (произведением) нечетких отношений и , заданных на X × Z и Z × Y, называется нечеткое отношение 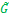= 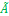◦ 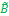на X × Y с функцией принадлежности

µ_G~(x,y) = 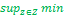(µ_A~(x,z), µ_B~(z,y)),

(x,y) 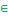X × Y, (x,z) 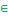X × Z, (z,y) 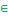Z × Y.

В случае конечных множеств X,Y,Z матрица нечеткого отношения 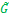= 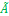◦ 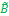рассчитывается как максминное произведение матриц 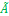и 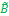. Эта операция выполняется как обычное произведение матриц, в котором поэлементное умножение заменено операцией минимума, а суммирование – операцией максимума. Аналогично определяются операции минимаксной и максимультипликативной композиции. Композиция играет ключевую роль в нечетком логическом выводе.