Формулировка задачи обучения с учителем, дискриминантный анализ

Задача обучения с учителем. На входе: обучающая, проверочная, контрольная выборка. По обучающей выборке программа строит решающие правила.

Вход: A^* - часть образа А

В^* - часть образа В

Найти: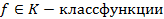

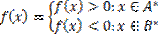
Предполагаем, что если A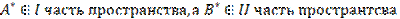^* , а => образ .

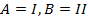4. Теорема Новикова

Если образы M и N не пересекаются, значит можно построить линейную разделяющую функцию за конечное время, такую что ρ_{обученя}(кач-ва) = 1

5. Нечеткая нейронная сеть

1 слой: функция введения нечеткости

2 слой: отображения совокупности нечетких правил

3 слой: приведение к четкости

Схема нечеткого вывода:

Входные значение -> Фазификация-> Нечеткие импликации (любые нечеткие операции)-> Результат в виде нечеткого множества -> Выходное значение (дефазификация)

Теорема о нечеткой аппроскимации— любая математическая система может быть аппроксимирована в нечеткой логике.

Определение математического нейрона -

Математический нейрон <==> нейрон, f(x) = sgn x = {1, если x>=0; 0, если x<0}

x = (sum w_i x_i + b)

1)Какое множество называется субнормальным? Как субнормальное множество можно привести к нормальному виду?

Если высота нечеткого множества меньше или больше 1, то такое множество называется субнормальным. От субнормального множества к нормальному можно перейти путем деления его функции принадлежности на высоту

2)Размерность максимального информативного пространства. Как определяется размерность рабочего информативного пространства?

Размерность максимального информативного пространства – Вычисляется по теореме ВАПНИКА:

Мощность обучающей выборки информативного пространства (количество векторов обучающей выборки) деленная на 3

Размерность рабочего информативного пространства определяется интуитивно, главное размерность раб пространства должна быть больше мин инф простр и меньше мак инф пространства
3)Перечислите свойства операций над нечеткими множествами.

u – Объединение

n – Пересечение

ϴ - Пустое множество

U – Универсальное множество

Коммутативность:

AnB = BnA

AuB = BuA

Ассоциативность:

(A n B) n C = A n (B n C)

( A u B) u C = A u (B u C)

Идемпотентность:

A n A = A

A u A = A

Дистрибутивность:

A n ( B u C) = (A n B) u (A n C)

A u (B n C) = (A u B) n (B u C)

A n ϴ = ϴ

A n U = A

A u U = U

Auϴ = A

Инволюция:

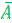= A

Теорема де Моргана:

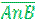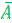= u

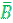
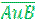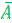= n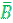

В отличие от четких множеств, для нечетких множеств в общем случае:

An 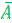!= ϴ

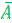Au !=U

4)Приведите определение высоты носителя

Высота нечеткого множества называется верхняя граница его функции принадлежности.

Носитель нечеткого множества – четкое подмножество универсального множества U, элементы, которого имеют не нулевые степени принадлежности.

5)Опишите физический смысл функции принадлежности. Отличие от вероятности.

Функция принадлежности μ ( x) нечеткого множества А=(X, μ ( x)) – это оценка качества (мера нечеткости) элемента x понятию А ( формализуемому нечетким множеством A ).

Вероятность P(A)=|A|/|Ώ| -- оценка количества элементов x ∈ A в группе Ώ

ПРИМЕР

Если элемент x ∈ X обладает свойством A , то μ ( x) = 1 , если же x∈ X определенно не обладает этим свойством A , то μ( x) = 0 .

Ответы на вопросы для аттестации