Логический синтез одноразрядного четверичного сумматора
ОЧС - это комбинационное устройство, имеющее 5 входов и 3 выхода:
·2 разряда одного слагаемого (множимого);
·2 разряда второго слагаемого (регистр результата);
·вход переноса из младшего ОЧС.
Принцип работы ОЧС описывается с помощью таблицы истинности
Разряды обоих слагаемых закодированы :0 - 11; 1 - 01; 2 - 10; 3 - 00.
 |  |  |  | p | П |  |  | Пример |
| 0+0+0=00 | ||||||||
| 0+0+1=01 | ||||||||
| 0+1+0=01 | ||||||||
| 0+1+1=02 | ||||||||
| x | x | x | 0+2+0=02 | |||||
| x | x | x | 0+2+1=03 | |||||
| x | x | x | 0+3+0=03 | |||||
| x | x | x | 0+3+1=10 | |||||
| 1+0+0=01 | ||||||||
| 1+0+1=02 | ||||||||
| 1+1+0=02 | ||||||||
| 1+1+1=03 | ||||||||
| x | x | x | 1+2+0=03 | |||||
| x | x | x | 1+2+1=10 | |||||
| x | x | x | 1+3+0=10 | |||||
| x | x | x | 1+3+1=11 | |||||
| 2+0+0=02 | ||||||||
| 2+0+1=03 | ||||||||
| 2+1+0=03 | ||||||||
| 2+1+1=10 | ||||||||
| x | x | x | 2+2+0=10 | |||||
| x | x | x | 2+2+1=11 | |||||
| x | x | x | 2+3+0=11 | |||||
| x | x | x | 2+3+1=12 | |||||
| 3+0+0=03 | ||||||||
| 3+0+1=10 | ||||||||
| 3+1+0=10 | ||||||||
| 3+1+1=11 | ||||||||
| x | x | x | 3+2+0=11 | |||||
| x | x | x | 3+2+1=12 | |||||
| x | x | x | 3+3+0=12 | |||||
| x | x | x | 3+3+1=13 |
В ОЧС на информационные входы не могут прийти комбинации (2,3) и поэтому в схеме появляются безразличные наборы.
Минимизацию выходов ОЧС проведем с помощью карт Карно-Вейче и алгоритма Рота.
Минимизация функции П картами Вейча:
 | |||||||||||
 | * | * | * | * | * | * |  * * | * | |||
 |  |  | |||||||||
 1 1 | |||||||||||
| * | * | * | * | * | * | * | * | ||||
 | |||||||||||
| p | p |
Минимизировав функцию, получим:
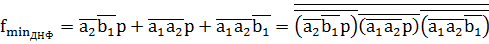
Минимизация функции 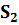 картами Карно:
картами Карно:
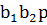 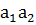 |   |  | ||||||
 * * | * | * | * | |||||
 01 01 | * |  * * |   |  * * |  * * | |||
| * | * |  1 1 | * | * | ||||
| * | * |  | * | * |
Минимизировав функцию, получим:
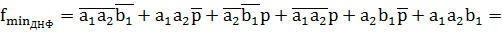

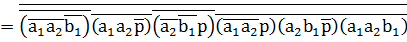
Минимизация функции 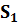 с помощью алгоритма Рота:
с помощью алгоритма Рота:
 Определим множество единичных кубов:
Определим множество единичных кубов:
L = 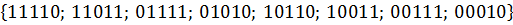
Для упрощения алгоритма Рота с помощью карты Карно проведём минимизацию безразличных наборов:
 | |||||||||||
 | * | * | * | * | * | * | * | * | |||
 | |||||||||||
| * | * | * | * | * | * | * | * | ||||
 | |||||||||||
| p | p |
Получим множество безразличных кубов:
N = 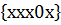
Сформируем множество:
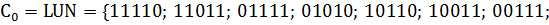
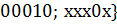
Первым этапом алгоритма Рота является нахождение множества простыхимпликант. Первый шаг умножения ( 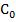 *
* 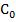 ) приведен в таблице:
) приведен в таблице:
| C0*C0 | xxx0x | ||||||||
| - | |||||||||
| 11y1y | - | ||||||||
| y111y | y1y11 | - | |||||||
| y1y10 | y101y | 01y1y | - | ||||||
| 1y110 | 1yy1y | yy11y | yyy10 | - | |||||
| 1yy1y | 1y011 | yyy11 | yy01y | 10y1y | - | ||||
| yy11y | yyy11 | 0y111 | 0yy1y | y011y | y0y11 | - | |||
| yyy10 | yy01y | 0yy1y | 0y010 | y0y10 | y001y | 00y1y | - | ||
| xxx0x | 111y0 | 110y1 | 011y1 | 010y0 | 101y0 | 100y1 | 001y1 | 000y0 | - |
| A0 | 1x110 | 1x011 | 0x111 | 0x010 | 101x0 | 100x1 | 001x1 | 000x0 | Ø |
| 111x0 | 110x1 | 011x1 | 010x0 |
В результате этой операции сформируем новое множество кубов:
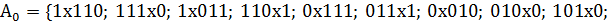
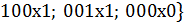
Множество 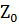 кубов, не участвовавших в образовании новых кубов, пустое.
кубов, не участвовавших в образовании новых кубов, пустое.
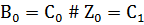
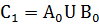
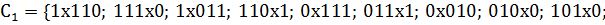
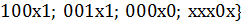
Выполним следующий шаг поиска простыхимпликант, выполнив 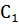 *
* 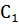 (Табл. 1)
(Табл. 1)
В результате этой операции сформируем новое множество кубов:
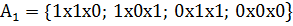
Множество 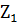 кубов, не участвовавших в образовании новых кубов, пустое.
кубов, не участвовавших в образовании новых кубов, пустое.
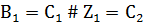
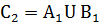
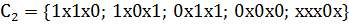
Выполним следующий шаг поиска простыхимпликант, выполнив 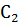 *
* 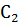 :
:
| C2*C2 | 1x1x0 | 1x0x1 | 0x1x1 | 0x0x0 |
| 1x1x0 | - | |||
| 1x0x1 | 1xyxy | - | ||
| 0x1x1 | yx1xy | yxyx1 | - | |
| 0x0x0 | yxyx0 | yx0xy | 0xyxy | - |
| xxx0x | 1x100 | 1x001 | 0x101 | 0x000 |
| A2 | Ø | Ø | Ø | Ø |
Множество 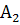 кубов пустое.
кубов пустое.
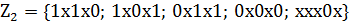
Множество простыхимпликант:
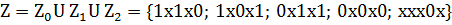
Поиск L-экстремалей.
| z#(Z-z) | 1x1x0 | 1x0x1 | 0x1x1 | 0x0x0 | xxx0x |
| 1x1x0 | - | 1x0x1 | 0x1x1 | 0x0x0 | 0xx0x |
| xx00x | |||||
| xxx01 | |||||
| 1x0x1 | 1x1x0 | - | 0x1x1 | 0x0x0 | 0xx0x |
| 0x00x | |||||
| xx000 | |||||
| 0xx01 | |||||
| xx101 | |||||
| 0x1x1 | 1x1x0 | 1x0x1 | - | 0x0x0 | 0x00x |
| 0xx00 | |||||
| 0x00x | |||||
| xx000 | |||||
| 0x001 | |||||
| 1x101 | |||||
| 0x0x0 | 1x1x0 | 1x0x1 | 0x1x1 | - | 0x001 |
| 0x100 | |||||
| 0x001 | |||||
| 1x000 | |||||
| 0x001 | |||||
| 1x101 | |||||
| xxx0x | 1x110 | 1x011 | 0x111 | 0x010 | - |
| Остаток | 1x110 | 1x011 | 0x111 | 0x010 | 0x001 |
| 0x100 | |||||
| 0x001 | |||||
| 1x000 | |||||
| 0x001 | |||||
| 1x101 |
| z#(Z-z) n L | ||||||||
| 1x110 | Ø | Ø | Ø | Ø | Ø | Ø | ||
| 1x011 | Ø | Ø | Ø | Ø | Ø | Ø | ||
| 0x111 | Ø | Ø | Ø | Ø | Ø | Ø | ||
| 0x010 | Ø | Ø | Ø | Ø | Ø | Ø | ||
| 0x001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 1x000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 1x101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
Откуда получим множество L-экстремалей 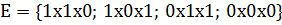
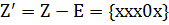
| L#E | ||||||||
| 1x1x0 | Ø | Ø | ||||||
| 1x0x1 | Ø | Ø | Ø | Ø | ||||
| 0x1x1 | Ø | Ø | Ø | Ø | Ø | Ø | ||
| 0x0x0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| Остаток | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
Получена единственная тупиковая форма:
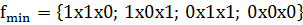
Проверка функции 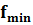 картами Карно:
картами Карно:
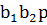 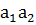 | ||||||||
 00 00 | * | * |  1 1 |  1 1 | * | * | ||
| * | * | * | * | |||||
| * |  * * |  | * |  * * | ||||
| * | * | * | * |
Минимизировав функцию, получим:
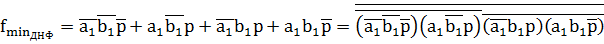
Построенная схема – Схема 3.
