Пос. Комсомольского Гулькевичского района Краснодарского края
Гончарова Татьяна Николаевна
Действительные числа.
1. Представьте обыкновенную дробь 3/7 в виде десятичной с точностью до сотых.
А. 0,40 В. 0,42
Б. 0,41 Г. 0,43
2. Соедините чертой обыкновенную дробь с равной ей десятичной дробью.
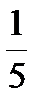
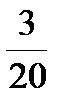
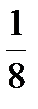
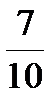
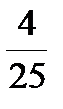
0,15 0,2 0,16 0,125 0,7
3. На координатной прямой найдите координату середины отрезка с концами в точках А(-7) и В(2).
Ответ:
4. Соедините чертой каждое выражение из верхней строки с равным ему выражением из нижней строки.
3/4 -0,3 3/10-0,8 0,25+4/5
0,8+1/4 0,75-3/10 -4/5+0,3
5. Продавец утверждает, что масса растительного масла в бутылке равна 1+0,02 л. Какое из значений массы не удовлетворяет этому утверждению?
А. 1010 мл Б. 980 мл В.995 мл Г. 975 мл
6. Выберите наибольшее из чисел: 3,833; 3,38; 3 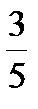 ; 3
; 3 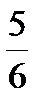 .
.
А. 3,833 Б. 3,38 В. 3 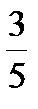 Г. 3
Г. 3 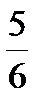
7. Укажите наименьшее из чисел: 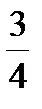 ; 0,7;
; 0,7; 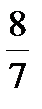 ; 0,8
; 0,8
А. 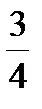 Б. 0,7 В.
Б. 0,7 В. 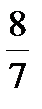 Г. 0,8
Г. 0,8
8. Расположите числа 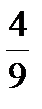 ,
, 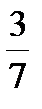 , 0,7 и 0,3 в порядке возрастания.
, 0,7 и 0,3 в порядке возрастания.
А. 0,3; 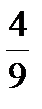 ;
; 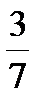 ; 0,7 Б. 0,3;
; 0,7 Б. 0,3; 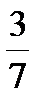 ;
; 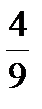 ; 0,7
; 0,7
В. 0,7; 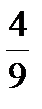 ;
; 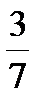 ; 0,3 Г. 0,3; 0,7;
; 0,3 Г. 0,3; 0,7; 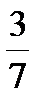 ;
; 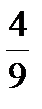 ;
;
9. Найдите значение выражения 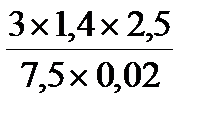 .
.
А. 70 Б. 7 В. 0,7 Г. 0,07
10. На координатной прямой отмечены противоположные числа: p и q. Сравните с нулём число r.
| p |
| r |
| q |
А. Сравнить нельзя Б. r >0
В. r =0 Г. r<0
11. Найдите наименьшее из следующих чисел
0,9; 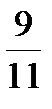 ;
; 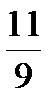 ;
; 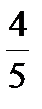 .
.
А. 0,9 Б. 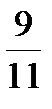 В.
В. 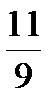 Г.
Г. 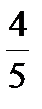
12. Десятичная запись некоторого натурального числа содержит 6 цифр. Найдите порядок этого числа.
А. 6 Б. 7
В. 5 Г. 60
13. Известно, что t2-1=0.Сравните числа t и 1/t.
14. О числах m, n, k, p известно, что m>n, p>k, k=m. Сравните числа
p и n.
15. Расположите в порядке возрастания числа 2√10; 6,5; √41.
16. Сравните числа 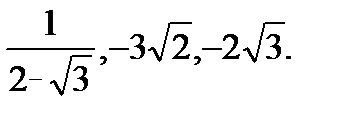
Ответы
| Г | 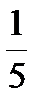 =0,2 =0,2 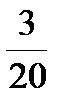 =0,15 =0,15 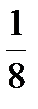 =0,125 =0,125 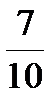 =0,7 =0,7 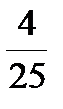 =0,16 =0,16 | -2,5 | 1-2 3-1 2-3 | Г | Г | Б. | Б. | А. | Г | Г | В | t = =1/t. | p > n | 2√10 √41 6,5 | 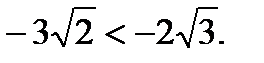 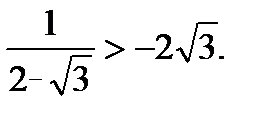 |
Проценты и части
1вариант
Часть 1.
При выполнении заданий 1 части запишите полученный ответ или обведите выбранный ответ.
1. В танцевальной студии число девочек относится к числу мальчиков, как 6:5. сколько можно составить пар, в каждую из которых входит мальчик и девочка, если всего в студии занимаются 66 человек?
Ответ:____________
2. Сумма трёх чисел равна 550. первое число составляет 28% суммы, второе – 24%. Найдите третье число.
Ответ:____________
3. В магазин привезли 480 кг яблок. Это составило 24% всех яблок, имеющихся на складе. Сколько кг яблок было на складе?
Ответ:____________
4. Некоторый товар поступил в продажу по цене 60 руб. В соответствии с принятыми в магазине правилами цена непроданного товара каждую неделю снижается на 10%. Сколько будет стоить товар на 12-й день, если не будет продан?
Ответ:____________
4. Перед Новым годом цены в магазине подарков были снижены на 25%. Некоторый товар до уценки стоил х рублей. Ученик записал четыре разных выражения для вычисления новой цены товара. Одно из них неверно. Какое?
А. х-0,25х Б. 0,75х В. х-0,25 Г. х- 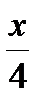
6. Укажите неверное утверждение.
А. 1/20 урожая меньше 20% этого урожая
Б. 1/6 урожая меньше 17% этого урожая
В. 1/3 урожая меньше 33% этого урожая
Г. 1/4 урожая меньше 40% этого урожая
Часть 2.
При выполнении заданий 2 части запишите развёрнутое решение задачи.
Из ведра в бочку перелили сначала половину имевшейся в нём воды, затем 1 л и, наконец, 20% остатка. В итоге количество воды в бочке увеличилось на 10%. Сколько воды было в ведре, если в бочке первоначально было 38 л воды?
2 вариант
Часть 1.
При выполнении заданий 1 части запишите полученный ответ или обведите выбранный ответ.
1. Со склада в первый день вывезли 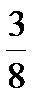 груза, во второй день -
груза, во второй день - 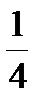 груза. Какая часть груза осталась на складе?
груза. Какая часть груза осталась на складе?
Ответ:____________
2. Сумма чисел равна 340. первое число составляет 15% суммы, второе 45%. Найдите третье число.
Ответ:____________
3. Государству принадлежат 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия за год составила 40 млн рублей. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?
Ответ:____________
4. Товар на распродаже уценили на 20%, при этом он стал стоить 680 рублей. Сколько стоил товар на распродаже?
Ответ:____________
5. Для смеси сухих трав взяли душицу и пустырник в отношении 13:7. Какой процент смеси составляет пустырник?
А. 7% Б. 70% В. 65% Г. 35%
6. Стоимость проезда на железнодорожном транспорте повысилась на 20%. Какова новая цена билета на электричку, если до повышения цен она составляла 40 р.?
А. 50 р. Б. 60 р. В. 32 р. Г. 48 р.
Часть 2.
При выполнении заданий 2 части запишите развёрнутое решение задачи.
Сосна на 50% выше ели. Если каждое дерево подрастёт ещё на 10 м, то сосна будет выше ели на 25%. Найдите первоначальную высоту ели.
Проценты и части
Ответы
1вариант
Часть 1.
- 30
- 264
- 2000
- 54
- В.
- В.
Часть 2.
Х л воды в ведре,
х/2+1+0,2(х/2-1)=0,1•38
Ответ: 5 л.
2 вариант
Часть 1.
- 3/8
- 136
- 16 млн рублей
- 850
- Г.
- Г.
Часть 2.
Х м- первоначальная высота ели,
1,5х+10=1,25(х+10)
Ответ: 10м
3. Преобразование алгебраических выражений
1вариант
Часть 1.
При выполнении заданий 1 части обведите выбранный вами ответ.
1. Упростить 3а(а-6)-(а-9)²
А. 2а²-81 Б. 2а²+81 В. 4а²-81 Г. 4а²+81
2. Выполните умножение 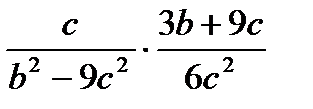 .
.
А. 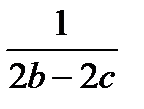 . Б.
. Б. 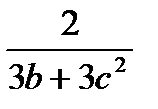 . В.
. В. 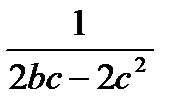 . С.
. С. 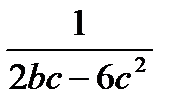 .
.
3. Сократите дробь 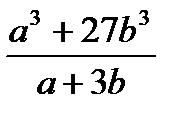 .
.
А. 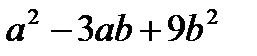 . Б.
. Б. 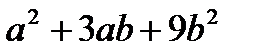 . В.
. В. 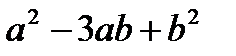 . Г.
. Г. 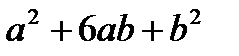 .
.
4. Сократите дробь 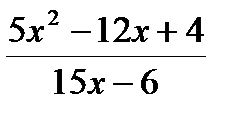
А. 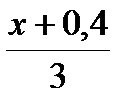 Б.
Б. 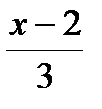 В.
В. 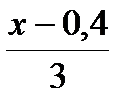 Г.
Г. 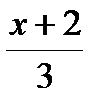
5. Найдите значение выражения 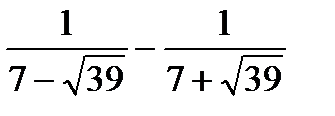 .
.
А. 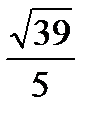 . Б.
. Б. 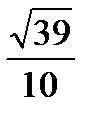 . В.
. В. 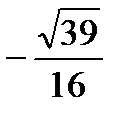 . Г. 0.
. Г. 0.
Часть 2.
При выполнении заданий 2 части запишите развёрнутое решение и ответ.
6. Упростите выражение
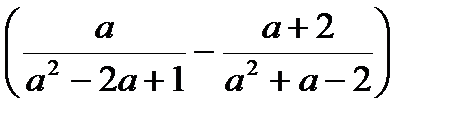 :
: 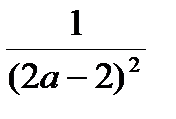 .
.
7. Выражение 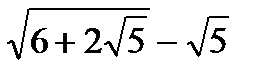 является целым числом. Найдите его.
является целым числом. Найдите его.
2 вариант
Часть 1.
При выполнении заданий 1 части обведите выбранный вами ответ.
1. Упростить (х+2)²-(х-2)(х+2)
А. 4х Б. 0 В. 4(х+2) Г. х+2
2. Найдите разность выражений 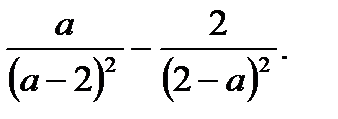
А. 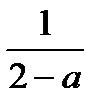 . Б.
. Б. 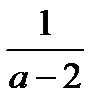 . В.
. В. 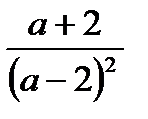 . Г.
. Г. 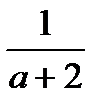 .
.
3. Сократите дробь 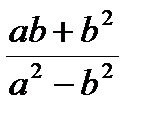
А.  Б.
Б. 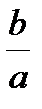 В.
В. 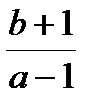 Г.
Г. 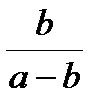
4. Сократите дробь 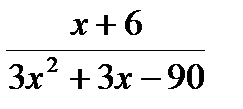
А. 3х-15 Б. 3х+15 В. 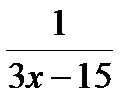 Г.
Г. 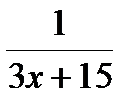
5. Сократите дробь 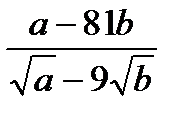 .
.
А. 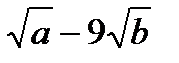 . Б.
. Б. 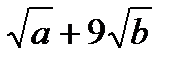 . В.
. В. 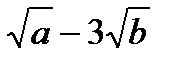 . Г.
. Г. 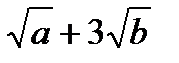 .
.
Часть 2.
При выполнении заданий 2 части запишите развёрнутое решение и ответ.
6. Упростите выражение
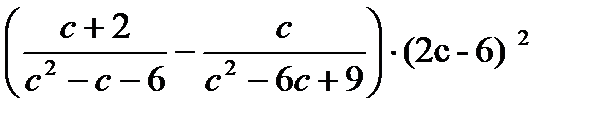
7. Упростите до целого числа выражение 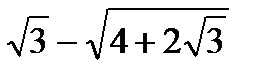 .
.
Преобразование алгебраических выражений
Ответы.
1вариант
| В | С | А | Б | А | -1 |
2 вариант
| В | Б | Г | В | Б | -12 | -1 |
Квадратные уравнения.
1вариант
Часть 1.
При выполнении заданий 1 части обведите выбранный вами ответ.
1. Дискриминант уравнения 7х2 + 6х + 1 = 0 равен:
1)32. 2)2. 3)-64. 4)8.
2. Корнем квадратного уравнения 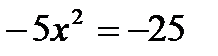 является число:
является число:
А.-5. Б. 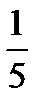 . В.
. В. 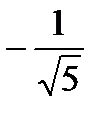 . Г.
. Г. 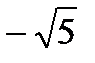
3. Разность большего и меньшего корней уравнения х2 - 9х + 14 = 0 равна:
1)5. 2)10. 3)3. 4) 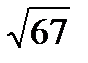 .
.
4. Не имеет корней уравнение:
1) 7х2 - 3х - 8 = 0. 2) 4х2 - 11х + 5 = 0.
3) 3х2 + 7х + 2 = 0. 4) 2х2 + х + 2 = 0.
5. Сумма и произведение корней уравнения х2 + 7х - 1 = 0 равны:
1) х1 + х2 = 7, х1 × х2 =1. 2) х1 + х2 = 1, х1 × х2 = 7.
3) х1 + х2 = -7, х1 × х2 = -1. 4) х1 + х2 = -1, х1 × х2 = 7.
6. Укажите верную формулу корней квадратного уравнения 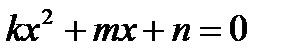 .
.
А. 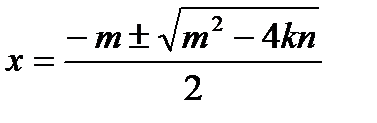 . Б.
. Б. 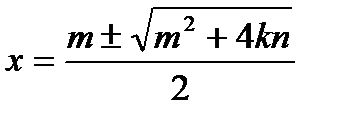 . В.
. В. 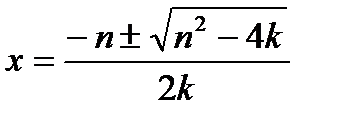 . Г.
. Г. 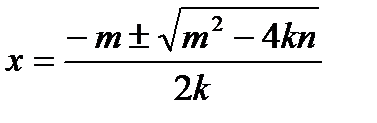
7. Если 7 – корень уравнения х2 + рх - 35 = 0, то значение р равно:
1)-2. 2)2. 3)12. 4)-12.
8. Если х1 и х2 - корни уравнения х2 + рх + q = 0, то
1) 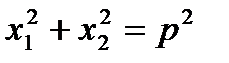 . 2)
. 2) 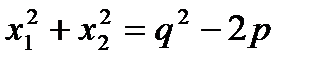 . 3)
. 3) 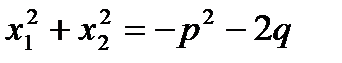 . 4)
. 4) 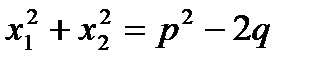 .
.
Часть 2.
При выполнении заданий 2 части запишите развёрнутое решение и ответ.
9. Решите уравнение 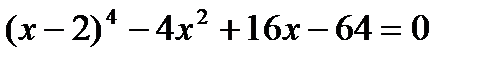 .
.
10. При каких значениях параметра 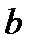 уравнение
уравнение 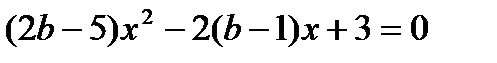 имеет единственное решение?
имеет единственное решение?
2вариант
Часть 1.
При выполнении заданий 1 части обведите выбранный вами ответ.
1. Дискриминант уравнения 5х2 - 3х + 2 = 0 равен:
1)19. 2)-1. 3)49. 4)-31.
2. Решите уравнение 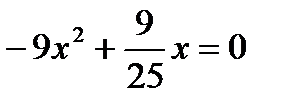 . В ответе укажите наименьший из его корней.
. В ответе укажите наименьший из его корней.
А. 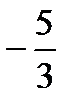 . Б.0. В.
. Б.0. В. 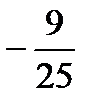 . Г.
. Г. 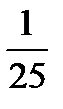 .
.
3. Разность большего и меньшего корней уравнения х2 + 5х - 24 = 0 равна:
1)1. 2)11. 3)7. 4)5.
4. Имеет два корня уравнение:
1) 5х2 + 2х + 1 = 0. 2) 5х2 - 2х + 1 = 0.
3) 5х2 + 2х -1 = 0. 4) х2 + 2х + 5 = 0.
5.Решите уравнение 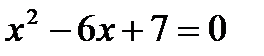 .
.
А. 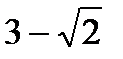 ;
; 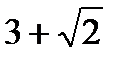 . Б.
. Б. 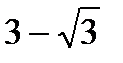 ;
; 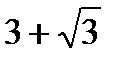 .
.
В. 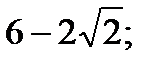
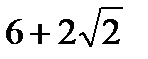 . Г.
. Г. 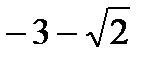 ;
; 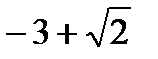 .
.
6. Каждое уравнение соотнесите с множеством его корней.
1) 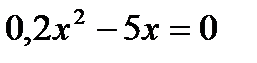 . 2)
. 2) 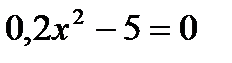 . 3)
. 3) 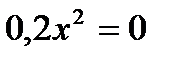 .
.
а)0. б)-5 и 5. в)0 и 25
7. Если х1 = -3, х2 = 4 - корни уравнения х2 + рх + q = 0, то
1) p = 1, q = -12. 2) p = -1, q = -12. 3) p = 12, q = 1. 4) p = -12, q = 1.
8. Если 11 – корень уравнения х2 -13x +q = 0, то значение q равно:
1) 22. 2) – 22. 3) – 264. 4) 264.
Часть 2.
При выполнении заданий 2 части запишите развёрнутое решение и ответ.
9.Произведение корней уравнения 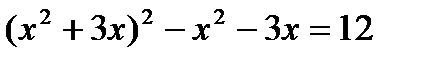 равно …
равно …
10. При каких значениях параметра 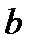 уравнение
уравнение 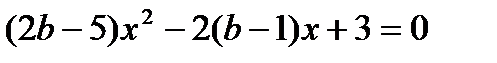 имеет два различных корня?
имеет два различных корня?
Квадратные уравнения.
Ответы
1вариант
Часть 1.
1. 4
2. Г
3. 1
4. 4
5. 3
6. Г
7. 1
8. 4
Часть 2.
9. 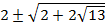
10. 2,5; 4
2вариант
Часть 1.
1. 4
2. Б
3. 2
4. 3
5. А
6. 1В; 2Б; 3А
7. 2
8. 1
Часть 2.
9. – 4
10. в 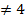
Системы уравнений.
1вариант
Часть 1.
При выполнении заданий 1 части запишите полученный ответ или обведите выбранный ответ.
1) 3ху = 1,
6х + у = 3.
А. ( 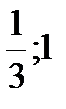 ), (
), ( 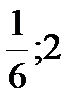 ) Б. (3; -15), (6; -33) В. (1;
) Б. (3; -15), (6; -33) В. (1; 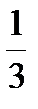 ), (2;
), (2; 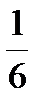 ) Г. (-15;3), ( - 33;6)
) Г. (-15;3), ( - 33;6)
2) 2х –у =1,
х +у = - 4.Ответ:____________
3) х + 2у =5,
ху = 2.
А. (1;2), (4; 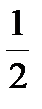 ), Б. ( 9; - 2), (6; -
), Б. ( 9; - 2), (6; - 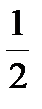 ) В. ( 9; - 2), (6; -
) В. ( 9; - 2), (6; - 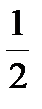 ), Г. ( 9; - 2), (6;
), Г. ( 9; - 2), (6; 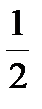 )
)
4) х 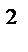 + у² = 17,
+ у² = 17,
х - у = - 5.Ответ:____________
5) 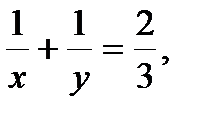
х + у = 8.Ответ:____________
6) 3х – у = - 10,
х 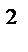 + у = 10.
+ у = 10.
А. (0; - 10);( 3 ; 49 ) Б. (10 ; 0);(19, 13) В. (0 ; 10);( 3 ; 19 ) Г. (0 ; 10) ; (- 3; 1)
7) х³ + у³ = 7,
х³ у³ = - 8.Ответ:____________
2 вариант
Часть 1.
При выполнении заданий 1 части запишите полученный ответ или обведите выбранный ответ.
1) 2х –у =1,
ху = 10.
А. ( 2; 5), Б. ( - 2; - 5) В. ( 2; 5), ( -2,5; - 4 ) Г. ( - 2; - 5), ( 1,25 ; 1,5 ).
2) 5х + 2у = 4,
2х +у = 1. Ответ:____________
3) х - у = 4,
ху + у² = 6.
А. (1;5), (- 3; 1), Б. ( 7; 3), (3; - 1) В. ( - 5; - 1), (- 1; 3), Г. ( 5; 1), (1; - 3)
4) х 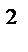 - у = - 2,
- у = - 2,
2х + у = 2.
А. (0; - 2) ;( - 2; 2) Б. ( 2; 0) ;( 6; - 2) В. ( 0; - 2) ;( - 6; 2) Г. ( 0;2) ;( - 2; 6)
5) х + у + ху = 14,
х + у - ху = - 2.
А. (- 4; - 2) ; ( 2 ; 4) Б. (2; 4) ; ( 4; 2) В. (- 4; - 2) ; ( - 2 ; - 4) Г. ( 2 ; 4)
6) х + у = 2,
ху = - 8. Ответ:____________
7) х - у = 1,
х³ - у³ = 7. Ответ:____________
Системы уравнений
Ответы.
1вариант
1. А
2. ( -1; -3)
3. А
4. ( -1; 4), (- 4; 1)
5. ( 6; 2), (2; 6)
6. Г
7. ( 2;-1), (-1; 2)
2вариант
1. Г
2. (2; -3)
3. Б
4. Г
5. Б
6. (4; -2), (-2; 4)
7. (3; 2); (0; -1)
Текстовые задачи.
1вариант
Часть 1.
При выполнении заданий 1 части запишите полученный ответ или обведите выбранный ответ.
1. Скорость пешехода от посёлка до станции, расстояние между которыми 4 км, была на 1 км/ч больше, чем ни обратном пути. Время его обратного пути на 12 минут больше. Чему равны скорости пешеходов? Пусть x км/ч – скорость пешехода от посёлка до станции. Какое из уравнений соответствует условию задачи?
А. 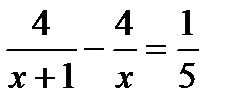 . Б.
. Б. 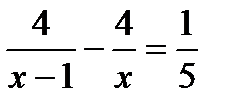 . В.
. В. 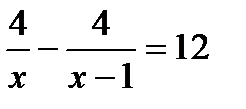 . Г.
. Г. 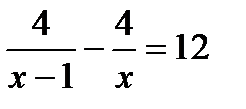 .
.
2. Моторная лодка прошла по течению реки 15 км и вернулась обратно, затратив на обратный путь на 40 минут больше. Скорость течения реки 3 км/ч. Пусть х км/ч — собственная скорость лодки. Какое из уравнений соответствует условию задачи?
А. 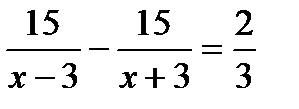 . Б.
. Б. 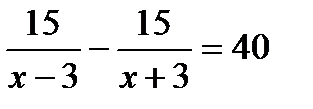 . В.
. В. 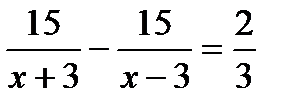 . Г.
. Г. 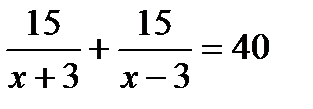 .
.
3. Найдите периметр прямоугольного участка площадью 192 м2, одна из сторон которого больше другой на 4 м. Ответ:____________
4. Один за другим с интервалом в 20 минут из города выехали в одном направлении два велосипедиста и встретились на расстоянии 15 км от города. Скорость движения второго велосипедиста была на 1 км/ч больше скорости первого. Пусть х км/ч — скорость движения первого велосипедиста. Какое из уравнений соответствует условию задачи? А. 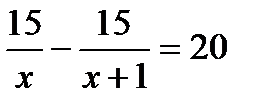 . Б.
. Б. 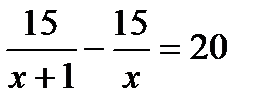 . В.
. В. 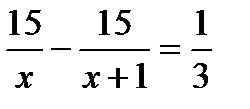 . Г.
. Г. 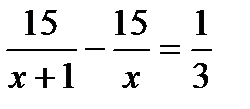 .
.
5. Две машины, работая одновременно, могут выполнить некоторую работу за 5 дней. Первая машина может справиться с этой работой на 24 дня быстрее второй. Какой объем работы выполнит первая машина? Пусть х дней – время работы первой машины. Какое из уравнений соответствует условию задачи?
А. 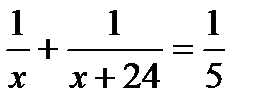 . Б.
. Б. 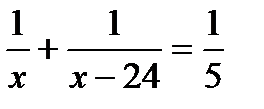 . В.
. В. 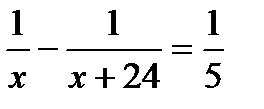 . Г.
. Г. 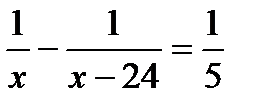 .
.
Часть 2.
При выполнении заданий 2 части запишите развёрнутое решение задачи.
6. Для распечатки 302 страниц были использованы две копировальные машины. Первая машина работала 8 мин., вторая-10 минут. Сколько страниц в минуту печатает первая машина, если первая печатает в минуту на 4 страницы больше, чем вторая?
7. На строительстве стены первый каменщик работал 5 дней один. Затем к нему присоединился второй, и они вместе закончили работу через 4 дня. Известно, что первому каменщику потребовалось бы на выполнение этой работы на 5 дней больше, чем второму. За сколько дней может построить эту стену первый каменщик, работая один?
8. Какое количество воды нужно добавить в 1 литр 9%-ного раствора уксуса, чтобы получить 3%-ный раствор?
9. На швейной фабрике израсходовали 204 м ткани на 24 пальто и 45 костюмов. На 24 пальто и 30 костюмов израсходовали 162 м. Сколько ткани расходуется на пошив одного пальто?
2вариант
Часть 1.
При выполнении заданий 1 части запишите полученный ответ или обведите выбранный ответ.
1. Скорость машины от поселка до станции была на 20 км/ч меньше, чем на обратном пути. Расстояние между пунктами 40 км, а время ее обратного пути на 10 минут меньше. Пусть x км/ч – скорость машины от поселка до станции. Какое из уравнений соответствует условию задачи?
А. 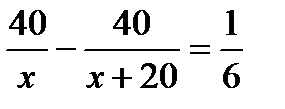 . Б.
. Б. 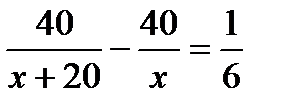 . В.
. В. 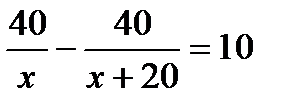 . Г.
. Г. 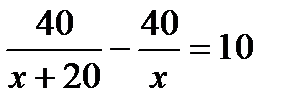 .
.
2. .Катер прошел 3 км по течению реки на 30 минут быстрее, чем 8 км против течения реки. Собственная скорость катера 15 км/ч. Пусть х км/ч — скорость течения реки. Какое из уравнений соответствует условию задачи?
А. 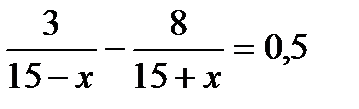 . Б.
. Б. 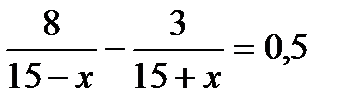 . В.
. В. 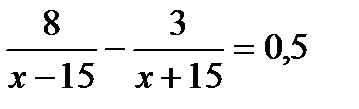 . Г.
. Г. 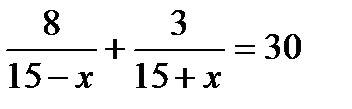 .
.
3. Найдите периметр прямоугольного участка площадью 91 м2, одна из сторон которого больше другой на 6 м. Ответ:____________
4. Две байдарки начали свое движение по озеру из одного пункта с интервалом в 10 минут и встретились через 2 км. Скорость движения первой байдарки была на 4 км/ч больше, чем скорость второй. Найдите скорости байдарок. Пусть х км/ч – скорость движения первой байдарки. Какое из уравнений соответствует условию задачи?
А. 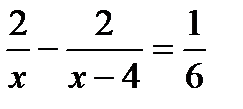 . Б.
. Б. 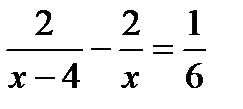 . В.
. В. 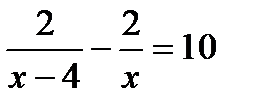 . Г.
. Г. 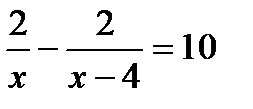 .
.
5. Две машины, работая одновременно, могут выполнить некоторую работу за 8 минут. Вторая машина может справиться с этой работой на 30 минут быстрее первой. Найдите время работы второй машины. Пусть х минут – время работы второй машины. Какое из уравнений соответствует условию задачи?
А. 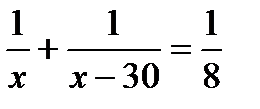 . Б.
. Б. 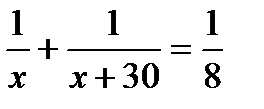 . В.
. В. 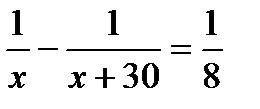 . Г.
. Г. 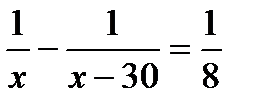 .
.
Часть 2.
При выполнении заданий 2 части запишите развёрнутое решение задачи.
6. Двое рабочих изготавливают по одинаковому количеству деталей. Первый выполнил эту работу за 6 ч, второй за 4 ч, так как изготовлял в час на 14 деталей больше первого. Сколько деталей изготовил второй рабочий?
7. За определенное время на заводе собирают 90 автомобилей. Первые три часа на заводе выполняли установленную норму, а затем стали собирать на один автомобиль в час больше. Поэтому за час до срока уже было собрано 95 автомобилей. Сколько автомобилей в час должны были собирать на заводе?
8. Какое количество воды надо добавить к 2 литрам 18%-ного раствора соли, чтобы получить 16%-ный раствор?
9. Имеются два куска сплава меди и цинка с процентным содержанием меди 30 и 55% соответственно. В каком отношении нужно взять эти сплавы, чтобы, переплавив, получить сплав, содержащий 40% меди?
Текстовые задачи.
Ответы
1вариант
Часть 1.
1. Б
2. А
3. 56
4. В
5. А
Часть 2.
1. 19 страниц
2. 15 дней
3. 2 литра
4. 2,8 метра
2вариант
Часть 1.
1. А
2. Б
3. 40
4. А
5. Б
Часть 2.
1. 42 детали
2. 6 автомобилей
3. 0,25 литра
4. 3:2
