Лабораторная работа 5. факторный анализ
Цель: углубление знаний по решению линейных задач выявления латентных признаков с последующей их интерпретацией с помощью процедур факторного анализа и анализа главных компонент.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Основные положения факторного анализа и анализа главных компонент.
Имеется множество из N объектов, каждый из которых описывается с помощью n-мерного вектора признаков, иначе переменных – x=(x1 , x2, …,xn )'. Если корреляционная матрица исходных переменных отлична от диагональной, то можно утверждать, что эти переменные зависят от меньшего числа других, непосредственно не измеряемых переменных y1, y2, … ,ym (m<n). Новые m переменные принято называть общими факторами. Поскольку в общем случае нельзя считать, что каждый из наблюдаемых признаков зависит лишь от m общих факторов, то постулируется, что исходный признак xi зависит также от “специфической”, характерной случайной компоненты ui..
Линейная модель факторного анализа в векторной форме имеет вид
x = Ay + u,
где A=(aij) – прямоугольная матрица размером n×m коэффициентов линейного преобразования, называемых нагрузками общих факторов на исходные признаки. Матрицу A называют матрицей факторных нагрузок или факторным отображением.
Основная теорема факторного анализа утверждает, что ковариационная матрица С исходных переменных может быть представлена как сумма ковариационной матрицы V характерных компонент и произведения матрицы факторных нагрузок на себя:
С = AA´ + V (5.1)
Соотношение получено в предположении, что общие факторы некоррелированы, их дисперсии равны единице, а характерные факторы не коррелируют между собой и с общими факторами.
Для того чтобы уменьшить влияние масштаба измерения переменных, обычно переходят к стандартизованным переменным. Стандартизация заключается в центрировании каждой исходной переменной с последующим делением отклонений от среднего значения переменной на ее среднеквадратическое отклонение. Для стандартизованных переменных ковариационная и корреляционная матрица совпадают.
Задачей факторного анализа является определение матрицы А. Число общих факторов должно быть минимальным, но в то же время таким, чтобы достаточно точно воспроизводить недиагональные элементы ковариационной либо корреляционной матрицы исходных переменных.
Задача факторного анализа решается в несколько этапов. На первом этапе оценивают дисперсии характерных факторов, а следовательно, и матрицу V, которая является диагональной в силе предпосылок факторного анализа. Соотношение (5.1) становится матричным уравнением относительно А:
AA´ = C – V . (5.2)
Решая на втором этапе тем или иным способом матричное уравнение (5.2), получают в итоге ортогональную матрицу А. Поскольку решение уравнения (5.2) не единственно, то возникает проблема выбора наиболее предпочтительного факторного отображения, что составляет содержание третьего этапа – вращения факторов. И, наконец, на последнем, четвертом, этапе оценивается значение общих факторов для каждого объекта. На практике обычно ограничиваются первыми тремя этапами, причем первый и второй этап выполняют одновременно.
Термин “вращение факторов” предполагает геометрическую интерпретацию факторного отображения А . В m-мерном пространстве общих факторов каждая i-я исходная переменная представляется вектором из начала координат в точку, координаты которой равны элементам i-й строки матрицы А. Очевидно, что длина подобным образом определенных векторов соответствует элементам главной диагонали матрицы C-V, а косинусы углов между векторами – недиагональным элементам корреляционной матрицы.
Для построения факторного отображения предложен ряд методов, однако основным следует признать метод главных факторов. В этом методе вначале полагают V=0. Матричное уравнение (1.2) (при V=0) имеет однозначное решение с вводом дополнительных ограничений, а именно: сумма квадратов нагрузок первого общего фактора должна составлять максимум оставшейся дисперсии и т.д. Решение этой задачи приводит к классической проблеме собственных значений.
Для оценки числа m общих факторов, подлежащих выделению, обычно используют сравнительно простой критерий “собственных значений” – выделять только те факторы, которые соответствуют собственным значениям корреляционной матрицы исходных признаков, большим единицы.
Исследование с помощью факторного анализа следует признать успешным, если выявлено не только число общих факторов, но и дано их толкование. Интерпретация общего фактора тем проще, чем “контрастнее” элементы матрицы А – либо близки к нулю, либо к единице(предполагается, что переменные стандартизованы). В этом случае при интерпретации общего фактора проще найти то общее, что есть у переменных с высокими нагрузками этого фактора.
Для оценки “контрастности” факторного отображения предложен ряд аналитических критериев. Квартимакс-критерий базируется на том факте, что при стремлении к нулю значений нагрузок будет убывать сумма квадратов попарных произведений элементов строк матрицы А. Варимакс-критерий максимизирует суммарную дисперсию квадратов нагрузок общих факторов по каждому исходному признаку, то есть дисперсию квадратов элементов столбца матрицы А.
Максимизация критерия обеспечивается последовательным поворотом каждой из возможных пар осей пространства общих факторов, в результате чего эти оси будут тяготить к сгущениям векторов, соответствующим исходным переменным.
Судить о том, содержит ли совокупность векторов подобное сгущение, можно с помощью критерия Бергмана. Для каждого общего фактора j(j=1,2,…,m) подсчитывают число переменных, для которых выполняется условие │aij/hi│≤ 0,1 (i= 1,2,…,n), где aij – элементы матрицы А, hi равняется квадратному корню из общности. В свою очередь , общность показывает дисперсии исходной переменной, приходящуюся на общие факторы, и вычисляется как:
h2i = a2i1 + a2i2 + … + a2im.
Найденное число, называемое числом нулевых нагрузок, сравнивают с табличным, соответствующим определенному числу факторов. Если число нулевых нагрузок больше указанного в таблице ( на выбранном уровне значимости), то можно считать, что этот фактор достаточно определен переменными и его можно интерпретировать.
В заключение отметим, прежде чем начинать факторный анализ целесообразно проверить, значимо ли отличается от единичной корреляционная матрица исходных признаков. В предположении, что исходные данные подчиняются многомерному нормальному распределению, можно воспользоваться статистикой
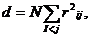 | 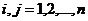 | ||
где rij - наддиагональные элементы корреляционной матрицы .
d подчиняется χ2- распределению с n(n-1)/2 степенями свободы. Этой же статистикой пользуются и для проверки значимости остаточной матрицы С-AkAk’ , полученной после выделения k общих факторов.
Если факторный анализ ориентирован на объяснение корреляции между исходными признаками, то анализ главных компонент ставит своей целью конструирование таких переменных, которые обладали бы свойством ортогональности и вбирали бы в себя максимум дисперсии исходных признаков. Обозначая новые переменные как z=(z1,z2,…zn)′, модель компонентного анализа можно записать в виде:
z = Ax,
где А – квадратная матрица искомых весовых коэффициентов.
Переменная z1 должна быть ориентированна по направлению максимально возможной дисперсии, вторая – по направлению максимально возможной дисперсии в подпространстве, ортогональном первому направлению, и т.д. Компоненты вектора z, удовлетворяющие этому требованию, называют главными компонентами.
Нахождение матрицы А приводит к проблеме собственных значений, при этом столбцы А совпадают с собственными векторами ковариационной матрицы исходных признаков С, а дисперсия i-й главной компоненты оказывается равной соответствующему собственному значению λ матрицы С. Суммарная дисперсия исходных признаков , равная следу матрицы С, равняется суммарной дисперсии главных компонент. Отсюда отношение λi к суммарной дисперсии характеризует вклад i-й главной компоненты в суммарную дисперсию исходных признаков. Задавшись некоторым порогом, для дальнейшего анализа оставляют те первые m главные компоненты, которые дают суммарный вклад не меньше заданного порога.
Аналитически доказано, что переход от исходного n-мерного пространства к m-мерному пространству главных компонент сопровождается наименьшими искажениями суммы квадратов расстояний между всевозможными парами рассматриваемых точек наблюдений. В случае m ≤ 3 данное свойство позволяет визуализировать исходные многомерные объекты с наименьшими искажениями.
КОНТРОЛЬНЫЕ ВОПРОСЫ
- Какова дисперсия i-й главной компоненты?
- Как найти главные компоненты, если ковариационная матрица исходных признаков диагональна?
- В чем различие между факторным анализом и анализом главных компонент?
- Какими критериями руководствуются при выборе числа общих факторов?
- Можно ли по факторному отображению восстановить ковариационную матрицу (корреляционную матрицу) исходных переменных?
- Какова дисперсия стандартизованной переменной?
- Как проверить значимость корреляционной матрицы?
- С какой целью проводят вращение факторов?
- В чем различие между квартимакс- и варимакс-критериями?
- Что показывает критерий Баргмана?
ЗАДАНИЕ
- Получить от преподавателя вариант исходных данных.
- Построить корреляционную матрицу исходных переменных и удостовериться, что она значимо отличается от единичной.
- Построить факторные отображения, используя критерии варимакс и квартимакс как для исходных, так и стандартизованных переменных.
- Дать содержательную интерпретацию выделенным общим факторам, выбрав подходящее факторное отображение п.3.
- Перейти в режим работы с главными компонентами. Построить диаграмму рассеяния исходных объектов.
- Сравните возможности интерпретации первых двух общих факторов и первых двух главных компонент.
- Отчет должен содержать:
- корреляционную матрицу исходных переменных и тест на ее значимость,
- факторные отображения и их геометрическое представление,
- диаграмму рассеяния в пространстве главных компонент,
- содержательную интерпретацию общих факторов для стандартизованных переменных.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА [5,12]
