Лабораторная работа 1. корреляционный анализ

Цель: углубление знаний в области корреляционного анализа, привитие навыков расчета и использования коэффициента корреляции Пирсона.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Основные положения корреляционного анализа

Для количественных переменных в качестве меры связи между двумя случайными величинами, измеренными в количественных шкалах, используют коэффициент парной корреляции Пирсона. Теоретический коэффициент корреляции r, определяемый для генеральной совокупности, задается как

,

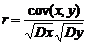где cov(x,y) = M[(x-M[x])(y-M[y])] = Mxy-MxMy – ковариация х и у, Dх, Dy –дисперсии соответствующих переменных. Для независимых случайных переменных М[ху] = М[х]М[у], следовательно, ковариация cov(x,y)и коэффициент корреляции r обращаются в нуль. Обратное в общем случае неверно. Поэтому при равенстве нулю коэффициента корреляции говорят, что соответствующие случайные величины некоррелированы.

Равенство нулю коэффициента корреляции еще не означает независимости переменных. Лишь в случае нормально распределенных случайных величин их некоррелированность влечет независимость. Независимость двух случайных величин означает равенство совместной плотности р(х,у) произведению частных плотностей

р(х,у)= р(х)р(у). (1)

Коэффициент корреляции r является параметром двумерного нормального закона. Можно показать, что соотношение (1) будет выполняться здесь тогда и только тогда, когда r=0.

Выборочный коэффициент корреляции есть

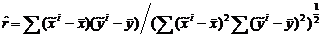. (2)

Основной практический интерес представляет проверка нуль-гипотезы H₀: r=0. Для нормально распределенных случайных величин х и у случайная величина

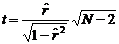(3)

при гипотезе Н₀подчиняется распределению Стьюдента с числом степеней свободы (ЧСС), равным N-2. Подставив в (3) выборочное значение 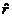, находят расчетное значение статистики Стьюдента t_p, которое сравнивают с табличным t_T при выбранном уровне значимости q (в инженерных расчетах обычно q=0,05) и ЧСС=N-2 . При t_p> t_T Н₀ отвергается.

Для порядковых переменных в качестве меры связи выступают коэффициент корреляции Спирмена 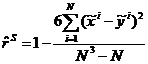либо коэффициент Кендэла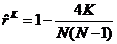

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В каком диапазоне находятся значения коэффициента корреляции?
2. Каков по знаку коэффициент корреляции между ростом и весом у молодых людей?
3. Каков по знаку коэффициент корреляции между временем разгона и мощностью автомобиля?
4. В чем различие в понятиях некоррелированность и независимость?
5. Какому закону распределения подчиняется выборочный коэффициент корреляции?
6. В каких случаях коэффициенты ранговой корреляции принимают граничные значения?

ЗАДАНИЕ

Рассчитать теоретическое и эмпирические значения коэффициента корреляции двух независимых случайных величин, а также двух случайных величин, одна из которых представляет сумму двух случайных величин. Исследовать влияние объема выборки на оценку коэффициента корреляции. Перевести количественные данные в порядковую шкалу и вычислить коэффициенты ранговой корреляции.

Методические указания

по выполнению лабораторной работы

1. Рассчитать теоретический коэффициент корреляции между случайной переменной х с нулевым математическим ожиданием М[х]=0 и единичной дисперсией D[х]=1 и величиной

z = x+аy, (4)

где y – случайная переменная с теми же характеристиками, что и у х, а – коэффициент, вычисляемый по формуле а = 0,5+0,3*N_ст (N_ст – порядковый номер студента в группе).

2. Открыть в Excel надстройку Анализ данных (закладка Сервис либо Данные).

3. Сформировать две выборки нормально распределенных случайных чисел х и у объемом 500 каждая, воспользовавшись макросом Генерация случайных чисел надстройки Анализ данных. Скопировать оба полученных столбца во второй лист Excel, воспользовавшись опцией Значения специальной вставки из меню Вставка. (Далее работать с листом 2).

4. Сформировать третью выборку в соответствии с выражением (4).

5. Запрограммировать формулу для расчета коэффициента корреляции (2). Для этого вначале подсчитать сумму, а затем среднее каждой выборки, завести по три столбца отклонений от среднего, квадратов отклонений от среднего, смешанных попарных произведений столбцов отклонений. Найти суммы в последних шести столбцах, с помощью которых затем вычислить коэффициенты корреляции между х и у, х и z, y и z, воспользовавшись выражением (2).

6. Вычислить коэффициенты корреляции с помощью макроса Корреляция Анализа данных.

7. Сравнить полученные результаты.

8. Оценить значимость коэффициентов корреляции.

9. Вычислить с помощью макроса Корреляция коэффициенты корреляции между первым и вторым рядами, взяв вначале первые 10, 100 и 250 членов выборки. Проверьте коэффициенты корреляции на значимость.

10. Выборки из 10 членов перевести в порядковую шкалу. Для этого постройте вариационный ряд для каждой из выборок, отсортировав данные в порядке возрастания. Присвойте каждому элементу исходной выборки ранг (место), который он занял в вариационном ряде.

11. Подсчитайте коэффициенты ранговой корреляции Спирмена 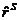и Кендэла 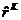и сравните с .

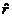Требования к отчету.

Отчет должен содержать титульный лист, вывод формулы по расчету коэффициента корреляции (п.1 задания), первые 30 и последние пять членов рядов X,Y,Z, их суммы и средние,а также оценки коэффициентов корреляции при разных объемах выборки, анализ результатов п.9 задания.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА [3, 12]