Плотность распределения двумерной случайной величины и ее свойства.
Неотрицательная функция f(x,y) называется плотностью распределения (плотностью вероятности) двумерной непрерывной СВ
| Z | Δ = | col(X,Y), |
если
| F(x,y) = | x ∫ -∞ | ( | y ∫ -∞ | f(x, y) dy | ) | dx = 1. |
При этом двумерная СВ Z называется непрерывной.
1) f(x, y) ≥ 0 для всех x, y О R1. Это вытекает из определения 1.
2)
| P(D) = | x2 ∫ x1 | y2 ∫ y1 | f(x, y) dy dx , где |
| D | Δ = | {x1 ≤ x ≤ x2, y1 ≤ y ≤ y2} . |
По свойству 7)F(x,y) и определению 1 имеем
| P(D) = F(x2,y2) - F(x2,y1) - F(x1,y2) + F(x1,y1) | Δ = |
| Δ = | x2 ∫ -∞ | y2 ∫ -∞ | f(x, y) dy dx - | x2 ∫ -∞ | y1 ∫ -∞ | f(x, y) dy dx - | x1 ∫ -∞ | y2 ∫ -∞ | f(x, y) dy dx + |
| + | x1 ∫ -∞ | y1 ∫ -∞ | f(x, y) dy dx = | x2 ∫ x1 | y2 ∫ y1 | f(x, y) dy dx . |
3)
| P(D) = | ∫ ∫ D | f(x, y) dx dy , |
где D - произвольная область на плоскости R2. Доказательство проведем для непрерывной f(x,y). Рассмотрим бесконечно малый прямоугольник
| ΔD | Δ = | {x ≤ X ≤ x + Δx, y ≤ Y ≤ y + Δy}. |
Согласно свойству 2)f(x,y) можно записать
| P(ΔD) = | x+Δx ∫ x | y+Δy ∫ y | f(x, y) dx dy = | | | по теореме о среднем значении | | | ≈ f(x, y) Δy Δx. |
Таким образом, элемент вероятности f(x,y)dxdy с точностью до бесконечно малых высшего порядка равен вероятности попадания двумерной СВ Z = col(X,Y) в бесконечно малый прямоугольник, прилегающий к точке (x,y). Так как произвольную область D М R2 можно представить с любой степенью точности в виде объединения конечного числа непересекающихся бесконечно малых прямоугольников ΔD, тоиз аксиомы A3 (см. замечание Л3.Р2.З2) следует формула для вероятности попадания СВ (X,Y) в D.
4)
| +∞ ∫ -∞ | +∞ ∫ -∞ | f(x, y) dy dx = 1, |
поскольку
| +∞ ∫ -∞ | +∞ ∫ -∞ | f(x, y) dy dx | Δ = | F(+∞,+∞) | 5)F(x,y) = | 1 . |
5)
| FX(x) = | x ∫ -∞ | +∞ ∫ -∞ | f(t, y) dy dt , FY(y) = | y ∫ -∞ | +∞ ∫ -∞ | f(x,y) dx dy; , |
где FX(x), FY(y) - функции распределения СВ X и Y. Например,
| FX(x) | 4)F(x,y) = | F(x,+∞) | Δ = | x ∫ -∞ | +∞ ∫ -∞ | f(x, y) dy dx . |
Для FY(y) утверждение доказывается аналогично.
6)
| fX(x) = | +∞ ∫ -∞ | f(x, y) dy , fY(y) = | +∞ ∫ -∞ | f(x, y) dx. |
Это вытекает из свойства 5) и определения Л4.Р3.О2.
7) Пусть СВ
| V | Δ = | φ(X,Y), |
где φ(x, y) - заданная скалярная функция аргументов x, y О R1 , такая что
| +∞ ∫ -∞ | +∞ ∫ -∞ | |φ(x, y)|f(x, y) dx dy < +∞. |
Тогда можно показать, что
| M[V] = | +∞ ∫ -∞ | +∞ ∫ -∞ | φ(x, y)f(x, y) dx dy. |
8) Для независимости непрерывных СВ X и Y необходимо и достаточно, чтобы выполнялось равенство
f(x, y) = fX(x)fY(y)
во всех точках непрерывности этих функций. Действительно, по определению плотности
| y ∫ -∞ | x ∫ -∞ | f(x, y) dx dy = F(x, y) = | || | в силу незави- симости | || | = FX(x)FY(y) = |
| Л4.Р3.О2 = | x ∫ -∞ | fX(x) dx | y ∫ -∞ | fY(y) dy = | x ∫ -∞ | y ∫ -∞ | fX(x)fY(y) dx dy . |
Откуда следует свойство 8).
Замечание 2. Свойство 6)f(x,y) позволяет по плотности вероятности двумерной СВ Z найти плотность вероятности СВ X и Y.
9) Если непрерывные СВ X и Y независимы, то справедлива формула свертки плотностей, т.е. плотность распределения СВ
| V | Δ = | X + Y |
имеет вид
| fV(v) = | +∞ ∫ -∞ | fX(x) fY(v-x) dx , |
где fX(x), fY(y) -- плотность распределения СВ X и Y. Пусть
| D | Δ = | {x, y : x + y ≤ v} . |
Тогда
| FV(v) | Δ = | P{X + Y ≤ v} | 2)f(x,y) = | ∫ ∫ D | f(x, y) dx dy | 8)f(x,y) = |
| = | ∫ ∫ D | fX(x),fY(y) dx dy = | +∞ ∫ -∞ | fX(x) ( | v-x ∫ -∞ | fY(y) dy) dx = | || | y | Δ = | t - x | || | = |
| = | +∞ ∫ -∞ | fX(x) ( | v ∫ -∞ | fY(t-x) dt) dx = | v ∫ -∞ | +∞ ∫ -∞ | fX(x)fY(t-x) dx dt . |
Понятие независимости для двумерных случайных величин.
Две дискретные случайные величины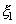 
и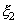 
называются независимыми, если для всех пар i, j выполняется соотношение
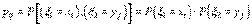
Условные распределения двумерной случайной величины.
Плотность двумерной нормально распределенной СВ Z при
| __________ √c11c22 - c122 > 0 |
определяется формулой
| f(x,y) = | __________ √c11c22 - c122 2π | exp{- | 1 | [c11(x - a)2 + 2c12(x - a)(y - b) + c22(y - b)2]}. |