Повторение испытаний. Схема Бернулли. Биноминальное распределение. Формула Пуассона.

Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А. Если в результате п опытов событие А наступает ровно т раз, то остальные п-т раз это событие не наступает. Событие А может появиться т раз в п испытаниях в различных комбинациях, число которых равно количеству сочетаний из п элементов по т. Это количество сочетаний находится по формуле:

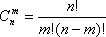
Вероятность каждой комбинации равна произведению вероятностей:

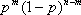
Применяя теорему сложения вероятностей несовместных событий, получаем Формулу Бернулли:

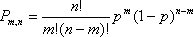
Если производится п независимых испытаний, в каждом из которых событие А может появиться с одинаковой вероятностью р в каждом из испытаний, то вероятность того, что событие не появится, равна q = 1 – p. Примем число появлений события в каждом из испытаний за некоторую случайную величину Х.

Вероятность каждого значения этой случайной величины можно найти по формуле Бернулли.

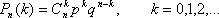
Эта формула аналитически выражает искомый закон распределения. Этот закон распределения называется биноминальным.

Формула распределение Пуассона:

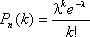
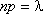(среднее число появлений события в n испытаниях).

Распределение Пуассона

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Пусть производится п независимых испытаний, в которых появление события А имеет вероятность р. Если число испытаний п достаточно велико, а вероятность появления события А в каждом испытании мало (p£0,1), то для нахождения вероятности появления события А k раз находится следующим образом. Сделаем важное допущение – произведение пр сохраняет постоянное значение:

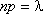
Практически это допущение означает, что среднее число появления события в различных сериях испытаний (при разном п) остается неизменным.По формуле Бернулли получаем:

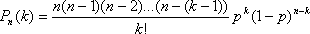
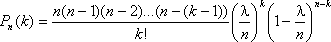
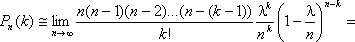
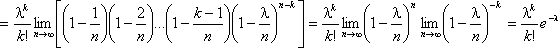
M[X] = D[X] = λ

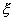9. Непрерывные случайные величины. Функция распределения и плотность распределения, и их свойства. Свойства математического ожидания и дисперсии. Квантили. Мода, медиана, асимметрия и эксцесс.

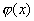Случайная величина называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция* , удовлетворяющая для любых значений x равенству:

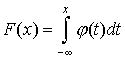
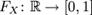
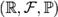
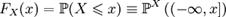Пусть дано вероятностное пространство , и на нём определена случайная величина X с распределением 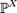. Тогда функцией распределения случайной величины X называется функция , задаваемая формулой:

Свойства:

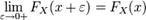F_X непрерывна справа:

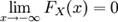F_X не убывает на всей числовой прямой.

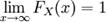
Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).

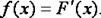
1) 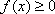Плотность распределения – неотрицательная функция:

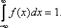
3) d\dx*F_x(x) = f_x(x) в точках непрерывности функции f_x(x).

Свойства математического ожидания:

1) М(а)=а

2) М(аХ)=а * М(х)

3) М(Х+Y) = М(Х)+М(Y)

Свойства дисперсии:

1) D(X) ≥ 0

2) D(c) = 0, c – const

3) D(cX) = c²D(X)

4) D(X+c) = D(x)

5) D(X+Y) = D(X) + D(Y)

Квантильюx_p (p-квантилью, квантилью уровня p) случайной величины x, имеющей функцию распределения F_x(x), называют решение x_p уравнения F_x(x)=p, p в промежутке (0, 1). Квантилиимеют свои названия:

· медиана - квантиль уровня 0.5;

· нижняя квартиль - квантиль уровня 0.25;

· верхняя квартиль - квантиль уровня 0.75;

· децили - квантили уровней 0.1,0.2, …, 0.9;

· процентили - квантили уровней 0.01,0.02, …, 0.99.

Модой М₀ дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.

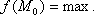
Медианой MD случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.

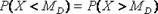
Начальным моментом порядка k случайной величины Х называется математическое ожидание величины Х^k

.

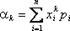
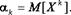Для дискретной случайной величины:

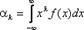
Для непрерывной случайной величины:

Начальный момент первого порядка равен математическому ожиданию.

Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом.

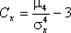
Нормальное распределение. Вероятность попадания в интервал, симметричный относительно математического ожидания. Ассиметрия и эксцесс распределения. Стандартизированное нормальное распределение и его свойство. Правило трех сигм.

Нормальное распределение - распределение вероятностей, которое задается функцией плотности распределения:

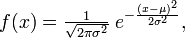
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

Вероятность попадания в интервал, симметричный относительно математического ожидания:

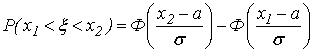, где a – математическое ожидание.

Найдём коэффициент асимметрии и эксцесс нормально распределённой случайной величины X.

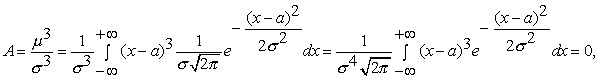
так как

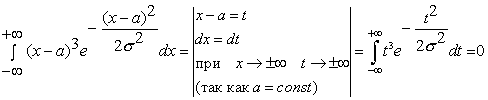
Таким образом, коэффициент асимметрии нормального распределения равен нулю (А=0).

Аналогично можно показать, что эксцесс нормального распределения также равен нулю.

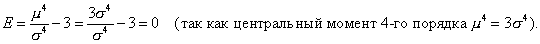
Если случайная величина распределена по закону N(0,1), то она называется нормированной или стандартизированной нормальной величиной. Функция распределения для нее имеет вид:

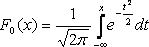
Ф(-х) = 1 – Ф(х)

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм. Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:

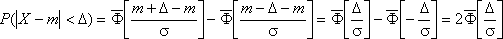
Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:

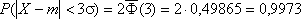
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую, чем утроенное среднее квадратичное отклонение, практически равна нулю.

Системы дискретных случайных величин. Таблица распределения. Независимость. Ковариация. Условные распределения.

Система двух дискретных случайных величин. 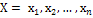; 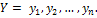(Х; Y) P [X= 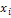; Y = 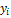] = 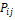(i=1, 2, …, n; j = 1, 2, …, m)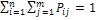

X/Y	Y1	Y2	…	Ym
X1	P11	P12	…	P1m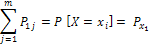
X2	P21	P22	…	P2m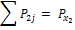
…	…	…	…	…	…
Xn	Pn1	Pn2	…	Pnm
			…

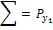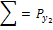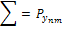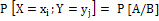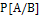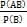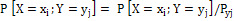; = ; - условное распределение.

Независимость координат – сл.в. Х и Y независимы тогда и только тогда, если 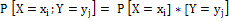(i=1,2,…,n; j=1,2,…,m). 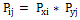- необходимое и достаточное условие независимости сл.в.

Ковариация - это мера линейной зависимости двух случайных величин. Коэффициент ковариации показывает степень зависимости между двумя величинами и есть ли она вообще. 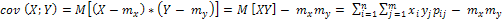. Свойства коэффициента ковариации: 1) если Х и Y независимы, то cov (X;Y) = 0, обратное не верно; 2) cov (aX; bY) = ab cov (X;Y).

Коэффициент корреляции: 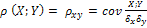Свойства: 1) 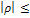1; 2) если Х и Y независимы, то cov = 0 и ρ = 0, обратное не верно! 3) если ρ=1, то между Х и Y имеется линейная связь (X и Y линейно зависимы); 4) если ρ 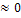, между Х и Y линейной зависимости нет (они не коррелированны).