Точечные оценки параметров распределения, их свойства.

Теория статистического оценивания рассматривает два основных вида оценки параметров распределений случайной величины: точечные и интервальные оценки. Точечный указывает лишь точку, около которой находится оцениваемый параметр; при интервальном находят интервал, который с определенной, как правило, большой вероятностью, задаваемой исследователем, накрывает неизвестное числовое значение параметра.

Точечной оценкойхарактеристики θ называют некоторую функцию результатов наблюдений, значения которой близки к неизвестной характеристике θ генеральной совокупности.

Сформулируем некоторые свойства, позволяющие разумным образом выбирать оценки.

1. Несмещенность оценки. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру генеральной совокупности:

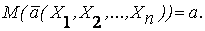
В противном случае оценка называется смещенной и допускает систематическую ошибку. Так, рассмотренное ранее среднее выборочное 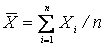является несмещенной оценкой среднего генерального. В то же время выборочная дисперсия 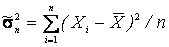- является смещенной оценкой генеральной дисперсии.

2. Состоятельность оценки. Оценка называется состоятельной, если она по вероятности с увеличением объема выборки п стремится к параметру генеральной совокупности:

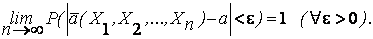
Это условие будет выполняться, если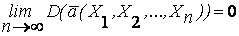

и оценка является несмещенной. Доказательство этого основано на неравенстве Чебышева.

3. Эффективность оценки. Если составлять множество несмещенных и состоятельных оценок, то эти оценки будут иметь разные дисперсии. Ясно, что, чем меньше будет дисперсия, тем меньше будет вероятность грубой ошибки при определении приближенного параметра генеральной совокупности. Поэтому нужно выбрать такую оценку, у которой дисперсия была бы минимальной: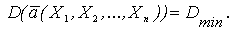

Такая оценка называется эффективной.

Оценка математического ожидания и дисперсии случайной величины при равноточных измерениях.

Доверительный интервал. Доверительная вероятность. Интервальная оценка математического ожидания.

Распределение Стьюдента.

Использование формул функций нормального распределения есть корректным , если аргумент выше указанных функций является беспрерывной величиной. Это означает, что расстояние между соседними измерениями есть бесконечно малыми и нуждается в бесконечном количестве наблюдений n. Для определения среднего квадратичного отклонения σмы должны решить уравнение: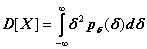

В случае , если нам известные только количество n наблюдений и их величины x₁, ..xn , так называемая выборка , то по нее найти дисперсию D[X] мы не сможем. За выборкой мы сможем найти только точечную дисперсию , которую обозначим s²_X и определим ее как : 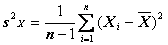где 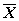среднее арифметическое значение измеренной величины: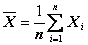

Переходя от точечной дисперсии отдельного наблюдения к точечной дисперсии среднего арифметического 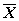с учетом количества наблюдений n имеем: ;

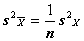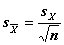
С учетом числа выборки n , получим = ;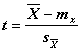

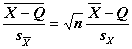Полученная случайная величина уже не будет иметь стандартное нормальное распределение!