Свойства коэффициента корреляции

1. Если и независимые случайные величины, то , однако обратное утверждение неверно.

2. Значения коэффициента корреляции заключены на отрезке или . При этом, чем ближе к единице, тем теснее связь между случайными величинами и .

3. Если , то и связаны линейной функциональной зависимостью.

В качестве оценки коэффициента корреляции генеральной совокупности используется выборочный коэффициент корреляции, который определяется по выборке.

О.4. Выборочным коэффициентом корреляции между случайными величинами и называется величина

,

где - варианты (наблюдавшиеся значения) признаков и ;

- частота пары вариант ;

- объем выборки (сумма всех частот);

- выборочные средние квадратические отклонения.

47.неравенство Чебышева)

Вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине меньше любого числа , не меньше чем , т.е.

.

Для события , противоположного событию , неравенство Чебышева может быть записано в виде:

.

Теорема 3.(теорема Чебышева)Если - попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа ), то, как бы мало ни было , вероятность неравенства:

будет как угодно близка к единице, если число случайных величин достаточно велико.

Замечание 1.Теорема Чебышева утверждает, что если рассматривается достаточно большое число случайных величин, имеющих равномерно ограниченные дисперсии и являющиеся независимыми, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.

Теорема 4.(частный случай теоремы Чебышева)

Если - попарно независимые случайные величины, имеющие одинаковые математические ожидание , и их дисперсии равномерно ограничены (не превышают постоянного числа ), то, как бы мало ни было , вероятность неравенства:

будет как угодно близка к единице, если число случайных величин достаточно велико.

Сущность теоремы Чебышева: хотя отдельные независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значения, близкие к определенному постоянному числу, а именно к числу . Другими словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало.

Значение теоремы Чебышева для практики:

При измерении некоторой физической величины производят несколько измерений и их среднее арифметическое принимают в качестве искомого размера. Теорема Чебышева указывает условия, при которых указанный способ может быть применен.

На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности исследуемых объектов.

Пусть выполнены условия схемы независимых испытаний Бернулли, причем 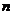достаточно велико.

48.теорема Бернулли) Если в каждом из 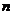независимых испытаний вероятность 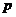события постоянна, то вероятность того, что отклонение относительной частоты от вероятности 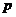по абсолютной величине будет сколь угодно малым, будет как угодно близка к единице если число испытаний достаточно велико, т.е.

.

Сущность теоремы Бернулли:теорема Бернулли позволяет предвидеть, какова примерно будет относительная частота появления события.