Геометрическое распределение

Пусть выполнены все условия схемы независимых испытаний. Испытания проводятся до 1-го появления события . Т. е. если событие появилось в 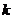-м (катом) испытании, то в предыдущих 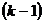испытаниях оно не появлялось.

Рассмотрим в качестве ДСВ число испытаний, которые необходимо провести до 1-го появления события . Т. о. возможные значения величины : .

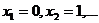Вероятности этих значений определяются по формуле:

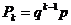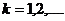, где . (1)

Если в эту формулу подставить последовательно вместо 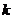: 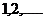, то получим геометрическую прогрессию с 1-м членом 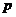и знаменателем ( ) : .

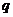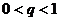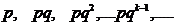O. 4.Закон распределения вероятностей ДСВ называется геометрическим, если вероятности ее возможных значений определяются по формуле (1) и образуют геометрическую прогрессию.

Гипергеометрическое распределение

Пусть имеется 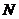элементов, среди которых 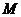обладают свойством . Случайным образом выбирается 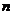элементов (выбор каждого элемента равновозможен), причем выборка осуществляется без возвращения.

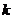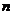Рассмотрим в качестве ДСВ количество элементов , обладающих свойством среди отобранных элементов. Т. е. величина может принимать значения: .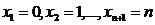

Вероятности этих значений определяются по формуле:

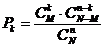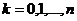, где . (2)

O. 5.Закон распределения вероятностей ДСВ называется гипергеометрическим, если вероятности ее возможных значений определяются по формуле (2).

Равномерное распределение

О.1. Закон распределения НСВ называется равномерным, если ее плотность распределения задается в виде:

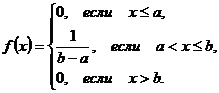
Свойства равномерного распределения

1. Зная плотность распределения, и используя формулу ,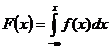

можно найти функцию распределения:

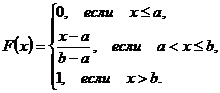
2. Если НСВ имеет равномерное распределение, то ее числовые характеристики могут быть найдены по формулам:

.

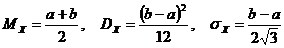3. Вероятность попадания равномерно-распределенной НСВ в интервал 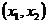можно определить по формуле:

.

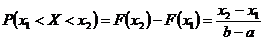Нормальное распределение

О.2. Закон распределения НСВ называется нормальным, если ее плотность распределения задается в виде:

,

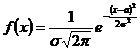где и 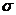- параметры нормального распределения.

Вероятностный смысл параметров нормального распределения:

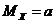- математическое ожидание,

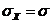- среднее квадратическое отклонение.

О.3. График плотности нормального распределения называют нормальной кривой или кривой Гаусса и он имеет вид:

О. 4. Нормальное распределение с параметрами 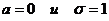называют нормированным (стандартным).

Свойства нормального распределения:

1. Зная плотность распределения и используя формулу ,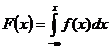

можно найти функцию распределения:

.

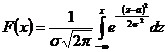2. Вероятность попадания нормально-распределенной НСВ в интервал 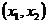определяется по формуле:

,

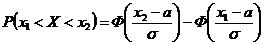где 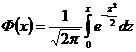- функция Лапласа.

3.Вероятность того, что отклонение нормально-распределенной НСВ от ее математического ожидания 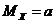по абсолютной величине будет меньше заданного числа , определяется по формуле:

.

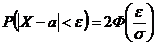Если 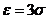, то .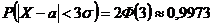

Правило трех сигм:

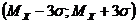Если НСВ распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, т. е. все значения НСВ попадают в интервал с вероятностью близкой к единице.

Теорема 1. (центральная предельная теорема Ляпунова)

Если НСВ представляет собой сумму очень большого числа взаимно независимых случайных величин, то влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение, близкое к нормальному.

Показательное распределение

О.1.Закон распределения НСВ называется показательным, если ее плотность распределения задается в виде:

,

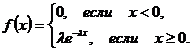где 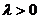- параметр показательного распределения.

Свойства показательного распределения:

1. Зная плотность распределения и используя формулу ,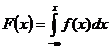

можно найти функцию распределения:

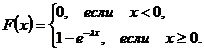
2. Если НСВ имеет показательное распределение, то ее числовые характеристики могут быть найдены по формулам:

.

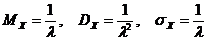3. Вероятность попадания показательно-распределенной НСВ в интервал 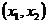определяется по формуле:

,

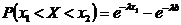где значения 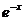определяются по таблице.

37.Распределение Пирсона 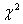– распределение случайной величины

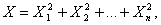
где случайные величины X₁, X₂,…, X_n независимы и имеют одно и тоже распределение N(0,1). При этом число слагаемых, т.е. n, называется «числом степеней свободы» распределения хи – квадрат.

38.Распределение t Стьюдента – это распределение случайной величины

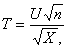
где случайные величины U и X независимы, U имеет распределение стандартное нормальное распределение N(0,1), а X – распределение хи – квадрат с n степенями свободы. При этом n называется «числом степеней свободы» распределения Стьюдента.

39.Распределение Фишера – это распределение случайной величины

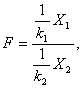
где случайные величины Х₁ и Х₂ независимы и имеют распределения хи – квадрат с числом степеней свободы k₁ и k₂ соответственно. При этом пара (k₁, k₂) – пара «чисел степеней свободы» распределения Фишера, а именно, k₁ – число степеней свободы числителя, а k₂ – число степеней свободы знаменателя.

Коэффициент корреляции

О.1. Корреляционная зависимость между случайными величинами и называется линейной, если обе функции регресси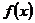и и 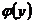являются линейными.

Для характеристики силы (тесноты) линейной корреляционной зависимости между случайными величинами используется коэффициент корреляции.

О.2. Коэффициентом корреляции называется безразмерная величина 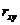, определяемая соотношением

,

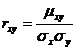где 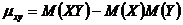-корреляционный момент;

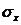и 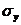- среднее квадратическое отклонение величин и

соответственно.

О.3. Две случайные величины и называются коррелированными, если их коэффициент корреляции отличен от нуля, иначе – некоррелированными.

Замечание 1. Две коррелированные случайные величины являются зависимыми, однако, обратное утверждение может не выполняться.