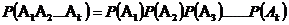Классическое определение вероятности и его свойства

Пусть в результате испытания может наступить конечное число 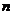равновозможных элементарных событий (исходов), причем среди них имеются 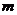таких исходов, которые ведут к появлению события . Эти событий называются благоприятствующими событию .

О. 2.(классическое определение) Вероятностью 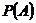события называется отношение числа элементарных событий благоприятствующих событию к числу всех элементарных событий:

,

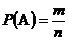где 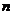- общее число элементарных событий,

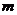- число элементарных событий благоприятствующих событию .

Свойства вероятности

Вероятность достоверного события равна единице, т. к.

;

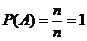Вероятность невозможного события равна нулю, т. к.

;

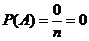Вероятность случайного события есть положительное число, заключенное между нулем и единицей, т. к.

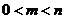, то .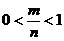

Недостатки классического определения.

1. Определение не применимо, если число элементарных исходов испытания бесконечно.

2. Часто не возможно представить результат испытания в виде совокупности элементарных событий.

3. Трудно указать основания, позволяющие считать события равновозможными. О равновозможности исходов опыта заключают из соображений симметрии.

Для преодоления 3 недостатка вводятся статистические вероятности, а для преодоления 1 недостатка – геометрические (вероятности попадания точки в область). Рассмотрим более подробно понятие статистической вероятности.

Статистическое определение вероятности. Относительная частота события

Пусть произошло 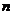испытаний, причем в этих испытаниях событие появилось 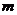раз. Число 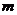называют абсолютной частотой события .

О. 3. Относительной частотой 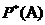события называется отношение числа испытаний, в которых событие появилось к общему числу проведенных испытаний

,

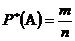где 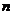- общее число испытаний,

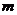- число появлений события .

Вероятность события может быть посчитана без проведения испытания, а относительная частота считается только в том случае, если испытание проведено фактически.

Если в одинаковых условиях проводят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает следующее свойство: в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа.

О. 4.(статистическое определение) Вероятностью события в данном испытании называется число 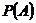, около которого группируется значения относительной частоты 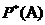при больших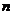

.

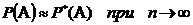Недостатки статистического определения.

Неоднозначность статистической вероятности.

Геометрическое определение вероятности.

Алгебра событий

О.1:Суммой двух событий и называется событие 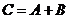, состоящее в появлении хотя бы одного из событий или .

Если события и совместные, то их сумма означает наступление или события , или события , или обоих событий и .

Если события и несовместные, то их сумма означает наступление или события , или события .

О. 2: Произведением двух событий и называется событие 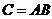, состоящее в одновременном появлении и .

Аналогично определяются сумма и произведение 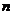событий.

Свойства суммы и произведения событий:

Пусть даны следующие события:

1) 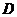- достоверное;

2) 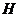- невозможное;

3) - случайное;

4) 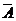- противоположное .

Тогда справедливы следующие соотношения:

1) ;

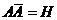2) ;

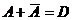3) ;

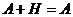4) ;

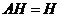5) ;

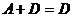6) .

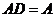8.Условной вероятностью события называется вероятность этого события, вычисленная в предположении, что событие уже произошло.

Обозначается 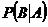или .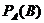

Условная вероятность события определяется аналогично.

Теорема 1. Если и независимые события, то их условные вероятности совпадают с обычными вероятностями, т. е.

,

.

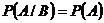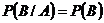Пусть даны два события и и требуется найти вероятность их совместного появления.

Теорема 2.Если и зависимые события, то вероятность их совместного появления (произведения) равна произведению вероятности одного из этих событий на условную вероятность другого, вычисленную при условии, что первое событие произошло, т. е.

,

.

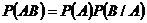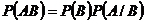Следствие: Вероятность совместного появления (произведения) нескольких зависимых событий 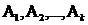равна произведению вероятности одного из этих событий на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие уже произошли, т. е.

.

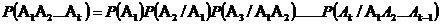Теорема 3.Если события и независимые, то вероятность их совместного появления (произведения) равна произведению их вероятностей, т. е.

.

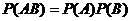Следствие:Вероятность совместного появления (произведения) нескольких независимых событий 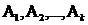равна произведению вероятностей данных событий, т. е.