Испытание. Событие. Классификация событий

Испытание. Событие. Классификация событий

О. 1: Испытание – это многократное воспроизведение одного и того же комплекса условий, при котором производится наблюдение.

Качественный результат испытания – событие.

О. 2:Множество взаимоисключающих исходов одного испытания называется множеством элементарных событий или элементарных исходов.

События обозначаются заглавными буквами латинского алфавита: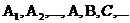

Наблюдаемые события (явления) можно подразделить на следующие три вида: достоверные, невозможные, случайные.

О. 3:Событие называется достоверным, если в результате испытания оно обязательно произойдет.

О. 4:Событие называется невозможным, если в результате испытания оно никогда не произойдет.

О. 5:Событие называется случайным, если в результате испытания оно может либо произойти, либо не произойти.

Случайные события (явления) можно подразделить на следующие виды: совместные, несовместные, противоположные, равновозможные.

О. 6:Два события называются совместными, если при одном испытании, появление одного из них не исключает появление другого.

О. 7:Два события называются несовместными, если при одном испытании, появление одного из них исключает появление другого.

О. 8:Несколько событий образуют полную группу в данном испытании, если они попарно несовместны и в результате испытания одно из этих событий обязательно появится.

О. 9:Два несовместных события, образующих полную группу называются противоположными.

Событие противоположное событию

обозначается .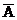

О. 10:События называются равновозможными, если есть основания считать, что одно из них не является более возможным, чем другое.

Понятие вероятности события

О. 1. Вероятностью события называется численная мера степени объективной возможности наступления события в данном испытании.

Выбор числового значения вероятности в конкретной задаче осуществляется либо при обработке результатов большого количества испытаний, либо предполагается теоретически ( например по свойству симметрии).

Классическое определение вероятности и его свойства

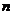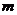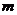Пусть в результате испытания может наступить конечное число равновозможных элементарных событий (исходов), причем среди них имеются таких исходов, которые ведут к появлению события . Эти событий называются благоприятствующими событию .

О. 2.(классическое определение) Вероятностью 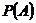события называется отношение числа элементарных событий благоприятствующих событию к числу всех элементарных событий:

,

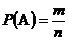где 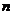- общее число элементарных событий,

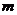- число элементарных событий благоприятствующих событию .

Свойства вероятности

Вероятность достоверного события равна единице, т. к.

;

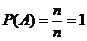Вероятность невозможного события равна нулю, т. к.

;

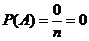Вероятность случайного события есть положительное число, заключенное между нулем и единицей, т. к.

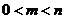, то .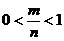

Недостатки классического определения.

1. Определение не применимо, если число элементарных исходов испытания бесконечно.

2. Часто не возможно представить результат испытания в виде совокупности элементарных событий.

3. Трудно указать основания, позволяющие считать события равновозможными. О равновозможности исходов опыта заключают из соображений симметрии.

Для преодоления 3 недостатка вводятся статистические вероятности, а для преодоления 1 недостатка – геометрические (вероятности попадания точки в область). Рассмотрим более подробно понятие статистической вероятности.

Алгебра событий

О.1:Суммой двух событий и называется событие 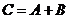, состоящее в появлении хотя бы одного из событий или .

Если события и совместные, то их сумма означает наступление или события , или события , или обоих событий и .

Если события и несовместные, то их сумма означает наступление или события , или события .

О. 2: Произведением двух событий и называется событие 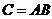, состоящее в одновременном появлении и .

Аналогично определяются сумма и произведение 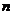событий.

Свойства суммы и произведения событий:

Пусть даны следующие события:

1) 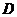- достоверное;

2) 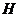- невозможное;

3) - случайное;

4) 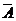- противоположное .

Тогда справедливы следующие соотношения:

1) ;

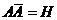2) ;

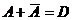3) ;

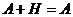4) ;

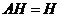5) ;

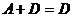6) .

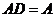8.Условной вероятностью события называется вероятность этого события, вычисленная в предположении, что событие уже произошло.

Обозначается 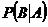или .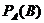

Условная вероятность события определяется аналогично.

Теорема 1. Если и независимые события, то их условные вероятности совпадают с обычными вероятностями, т. е.

,

.

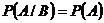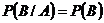Пусть даны два события и и требуется найти вероятность их совместного появления.

Теорема 2.Если и зависимые события, то вероятность их совместного появления (произведения) равна произведению вероятности одного из этих событий на условную вероятность другого, вычисленную при условии, что первое событие произошло, т. е.

,

.

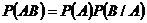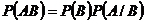Следствие: Вероятность совместного появления (произведения) нескольких зависимых событий 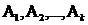равна произведению вероятности одного из этих событий на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие уже произошли, т. е.

.

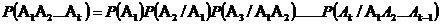Теорема 3.Если события и независимые, то вероятность их совместного появления (произведения) равна произведению их вероятностей, т. е.

.

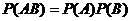Следствие:Вероятность совместного появления (произведения) нескольких независимых событий 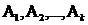равна произведению вероятностей данных событий, т. е.

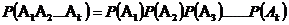
Формула полной вероятности

Теорема.Если событие может наступить только при условии появления одного из несовместных событий 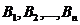, которые образуют полную группу, то вероятность события равна сумме произведений каждого из этих событий на соответствующие условные вероятности события , т. е.

.

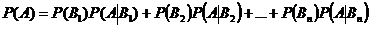Поскольку заранее не известно, какие из событий 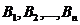наступят, то их называют гипотезами.

14.

Пусть проводится 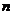независимых испытаний, в каждом из которых возможно только два исхода: либо событие появится, либо нет.

Условимся считать, что вероятность события в каждом испытании одна и та же и равна .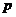

Тогда вероятность ненаступления события в каждом испытании так же постоянна и равна .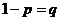

Формула Бернулли

О. 1.Если проводится несколько испытаний, причем вероятность появления события в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимымиотносительно события .

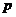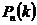Теорема 1. Если вероятность наступления события в каждом из независимых испытаний постоянна, то вероятность того, что в 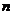независимых испытаниях событие появится ровно 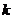раз, вычисляется по формуле

.

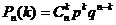Формула Пуассона

Если число испытаний 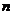достаточно велико, а вероятность появления события в каждом испытании постоянна и равна 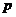, причем 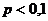, то применение формулы Муавра-Лапласа становится невозможным.

Теорема 3. Если вероятность 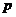появления события в каждом испытании стремится к нулю при неограниченном увеличении числа испытаний, причем произведение 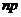сохраняет постоянное значение, т. е. 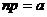, то вероятность 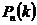того, что в 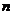независимых испытаниях событие появится 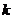раз удовлетворяет предельному равенству:

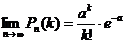(2).

Строго говоря, условие теоремы 2: 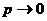при 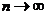, нарушает исходные предпосылки в схеме независимых испытаний Бернулли, в которой 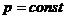. Однако, если вероятность 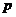постоянна и достаточно мала, а число 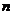испытаний велико, причем произведение 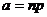незначительно, то из предельного равенства (2) можно записать приближенную формулу Пуассона:

.

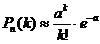Числовые характеристики НСВ

Пусть непрерывная случайная величина задана плотностью распределения 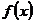. Тогда аналогично ДСВ для НСВ могут быть определены числовые характеристики.

О.1. Математическим ожиданием 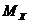НСВ , возможные значения которой принадлежат всей оси 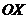, называют определенный интеграл:

.

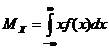O.2.Дисперсией 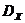НСВ , возможные значения которой принадлежат всей оси 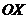, называется значение интеграла

.

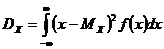Замечание 1. Свойства математического ожидания и дисперсии ДСВ сохраняются и для НСВ.

Замечание 2.На практике для вычисления дисперсии удобно пользоваться формулой: .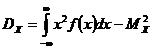

O.3.Средним квадратическим отклонением 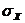НСВ называется корень квадратный из дисперсии, т.е.

.

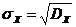О.4.Модой 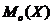НСВ называется такое значение этой величины, плотность вероятности которого максимальна.

O.5.Медианой 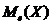НСВ называется такое значение этой величины, что выполняется равенство:

.

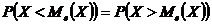27.Математическим ожиданием 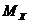НСВ , возможные значения которой принадлежат всей оси 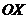, называют определенный интеграл:

.

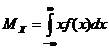Модой 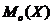НСВ называется такое значение этой величины, плотность вероятности которого максимальна.

O.5.Медианой 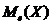НСВ называется такое значение этой величины, что выполняется равенство:

.

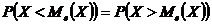28. Дисперсией 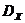НСВ , возможные значения которой принадлежат всей оси 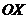, называется значение интеграла

.

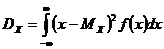Замечание 1. Свойства математического ожидания и дисперсии ДСВ сохраняются и для НСВ.

Замечание 2.На практике для вычисления дисперсии удобно пользоваться формулой: .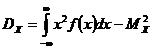

O.3.Средним квадратическим отклонением 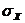НСВ называется корень квадратный из дисперсии, т.е.

.

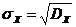Биномиальное распределение

Пусть выполнены все условия схемы независимых испытаний Бернулли.

Рассмотрим в качестве ДСВ число появлений события в этих испытаниях. Т. е. величина может принимать значения: .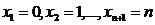

Вероятности этих значений определяются по формуле Бернулли:

, .

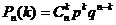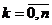О. 2.Закон распределения вероятностей ДСВ называется биномиальным, если вероятности ее возможных значений определяются по формуле Бернулли.

31.Пуассоновское распределение

Пусть в схеме независимых испытаний Бернулли число испытаний достаточно велико ( 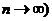, а вероятность появления события очень мала .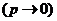

Рассмотрим в качестве ДСВ число появлений события в этих испытаниях. Т. е. величина может принимать значения: .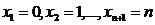

Вероятности этих значений определяются по формуле Пуассона:

, .

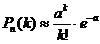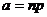О. 3.Закон распределения вероятностей ДСВ называется пуассоновским, если вероятности ее возможных значений определяются по формуле Пуассона.

Равномерное распределение

О.1. Закон распределения НСВ называется равномерным, если ее плотность распределения задается в виде:

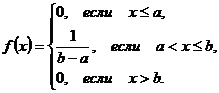
Нормальное распределение

О.2. Закон распределения НСВ называется нормальным, если ее плотность распределения задается в виде:

,

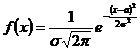где и 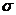- параметры нормального распределения.

Вероятностный смысл параметров нормального распределения:

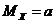- математическое ожидание,

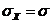- среднее квадратическое отклонение.

О.3. График плотности нормального распределения называют нормальной кривой или кривой Гаусса и он имеет вид:

О. 4. Нормальное распределение с параметрами 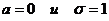называют нормированным (стандартным).

Свойства нормального распределения:

1. Зная плотность распределения и используя формулу ,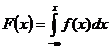

можно найти функцию распределения:

.

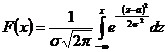2. Вероятность попадания нормально-распределенной НСВ в интервал 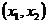определяется по формуле:

,

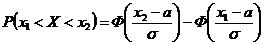где 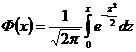- функция Лапласа.

3.Вероятность того, что отклонение нормально-распределенной НСВ от ее математического ожидания 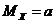по абсолютной величине будет меньше заданного числа , определяется по формуле:

.

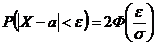Если 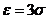, то .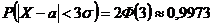

Правило трех сигм:

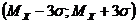Если НСВ распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, т. е. все значения НСВ попадают в интервал с вероятностью близкой к единице.

Теорема 1. (центральная предельная теорема Ляпунова)

Если НСВ представляет собой сумму очень большого числа взаимно независимых случайных величин, то влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение, близкое к нормальному.

Показательное распределение

О.1.Закон распределения НСВ называется показательным, если ее плотность распределения задается в виде:

,

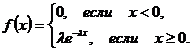где 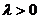- параметр показательного распределения.

Свойства показательного распределения:

1. Зная плотность распределения и используя формулу ,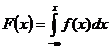

можно найти функцию распределения:

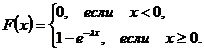
2. Если НСВ имеет показательное распределение, то ее числовые характеристики могут быть найдены по формулам:

.

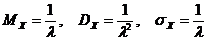3. Вероятность попадания показательно-распределенной НСВ в интервал 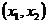определяется по формуле:

,

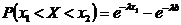где значения 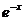определяются по таблице.

37.Распределение Пирсона 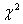– распределение случайной величины

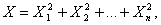
где случайные величины X₁, X₂,…, X_n независимы и имеют одно и тоже распределение N(0,1). При этом число слагаемых, т.е. n, называется «числом степеней свободы» распределения хи – квадрат.

38.Распределение t Стьюдента – это распределение случайной величины

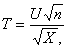
где случайные величины U и X независимы, U имеет распределение стандартное нормальное распределение N(0,1), а X – распределение хи – квадрат с n степенями свободы. При этом n называется «числом степеней свободы» распределения Стьюдента.

39.Распределение Фишера – это распределение случайной величины

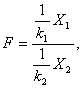
где случайные величины Х₁ и Х₂ независимы и имеют распределения хи – квадрат с числом степеней свободы k₁ и k₂ соответственно. При этом пара (k₁, k₂) – пара «чисел степеней свободы» распределения Фишера, а именно, k₁ – число степеней свободы числителя, а k₂ – число степеней свободы знаменателя.

Коэффициент корреляции

О.1. Корреляционная зависимость между случайными величинами и называется линейной, если обе функции регресси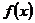и и 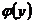являются линейными.

Для характеристики силы (тесноты) линейной корреляционной зависимости между случайными величинами используется коэффициент корреляции.

О.2. Коэффициентом корреляции называется безразмерная величина 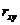, определяемая соотношением

,

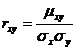где 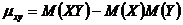-корреляционный момент;

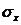и 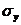- среднее квадратическое отклонение величин и

соответственно.

О.3. Две случайные величины и называются коррелированными, если их коэффициент корреляции отличен от нуля, иначе – некоррелированными.

Замечание 1. Две коррелированные случайные величины являются зависимыми, однако, обратное утверждение может не выполняться.

Испытание. Событие. Классификация событий

О. 1: Испытание – это многократное воспроизведение одного и того же комплекса условий, при котором производится наблюдение.

Качественный результат испытания – событие.

О. 2:Множество взаимоисключающих исходов одного испытания называется множеством элементарных событий или элементарных исходов.

События обозначаются заглавными буквами латинского алфавита: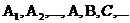

Наблюдаемые события (явления) можно подразделить на следующие три вида: достоверные, невозможные, случайные.

О. 3:Событие называется достоверным, если в результате испытания оно обязательно произойдет.

О. 4:Событие называется невозможным, если в результате испытания оно никогда не произойдет.

О. 5:Событие называется случайным, если в результате испытания оно может либо произойти, либо не произойти.

Случайные события (явления) можно подразделить на следующие виды: совместные, несовместные, противоположные, равновозможные.

О. 6:Два события называются совместными, если при одном испытании, появление одного из них не исключает появление другого.

О. 7:Два события называются несовместными, если при одном испытании, появление одного из них исключает появление другого.

О. 8:Несколько событий образуют полную группу в данном испытании, если они попарно несовместны и в результате испытания одно из этих событий обязательно появится.

О. 9:Два несовместных события, образующих полную группу называются противоположными.

Событие противоположное событию

обозначается .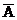

О. 10:События называются равновозможными, если есть основания считать, что одно из них не является более возможным, чем другое.

Понятие вероятности события

О. 1. Вероятностью события называется численная мера степени объективной возможности наступления события в данном испытании.

Выбор числового значения вероятности в конкретной задаче осуществляется либо при обработке результатов большого количества испытаний, либо предполагается теоретически ( например по свойству симметрии).