Теорема о скоростях точек в плоском движении

Скорость любой точки плоской фигуры при плоскопараллельном движении равна геометрической сумме скорости выбранного полюса и скорости точки во вращательном движении фигуры вокруг полюса.

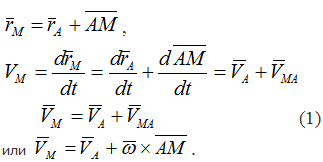
Производная от вектора AM, постоянного по величине и переменного по направлению, численно равна скорости точки М при вращении ее вокруг точки А.

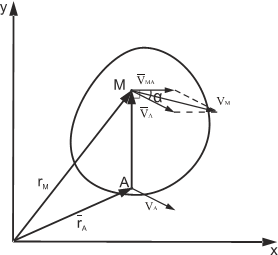
Рис. 1.3

Вектор V_MA=ω⋅ AM перпендикулярен отрезку АМ.

Численную величину скорости точки М можно получить, если воспользоваться теоремой косинусов

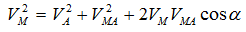
или спроецировать векторное равенство (1) на выбранные оси координат

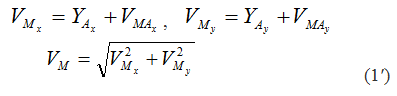
Следствие из теоремы о скоростях точек в ППД

Из теоремы о скоростях точек плоской фигуры следует, что проекции скоростей точек плоской фигуры на ось, проходящую через эти точки, равны. Это легко показывается в рассуждениях:

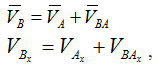
так как V_BA⊥ AB, то и проекция V_BA на ось АХ равна нулю.

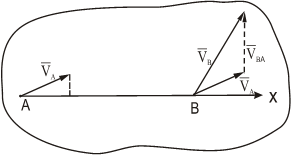
Рис. 1.4

Следовательно, V_Bx=V_Ax.

Мгновенный центр скоростей (МЦС)

Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра.

В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нолю. Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например P_V, C_V.

При определении положения МЦС скорость любой точки может быть записана: V_M=V_CV+V_MCV, где точка С_Vвыбрана за полюс. Поскольку это МЦС и V_CV=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей.

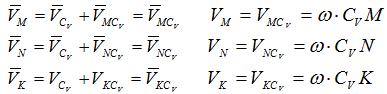
Из рис. 1.5 видно, что мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных к скоростям точек, при этом всегда справедливо соотношение

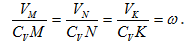
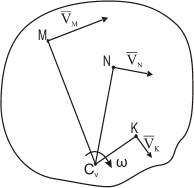
Рис. 1.5

На нижеприведенных рисунках показаны примеры определения положения мгновенного центра скоростей и приведены формулы для расчета скоростей точек.

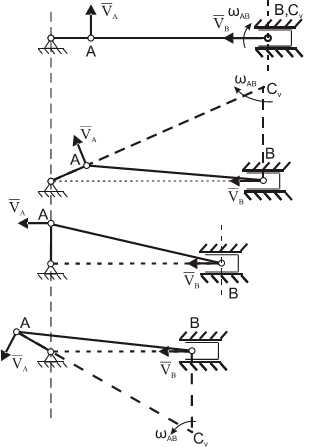
Рис. 1.6

Для рисунка 1.6:

1. С_V совпадает с точкой В V_B=0. Шатун АВ вращается вокруг точки В
   
2. 
   
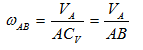
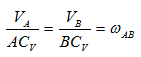
3. МЦС лежит в «бесконечности»
   
4. 
   

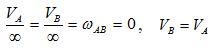
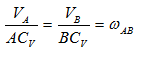
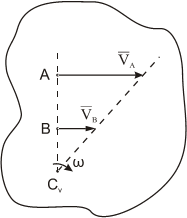
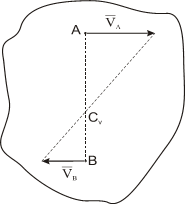
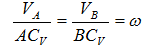
Рис. 1.7

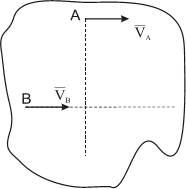
Рис. 1.8

здесь V_BII V_A

В этом случае МЦС находится в “бесконечности”, т.е

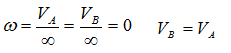
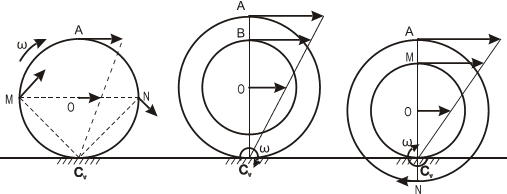
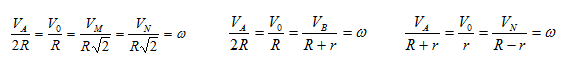
Рис. 1.9

Формулы справедливы при отсутствии проскальзывания в точке СV.

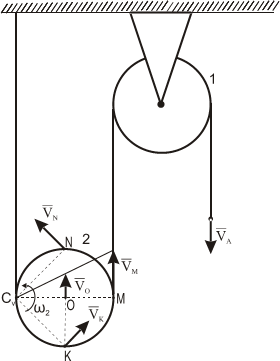
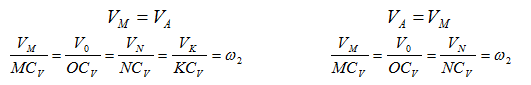
Рис. 1.10

Теорема об ускорении точек в плоском движении

При плоском движении ускорения точек определяются согласно следующей теореме:

Из выражения V_M=V_A+V_MA (или V_M=V_A + ω ⋅ AM ) путем дифференцирования получаем

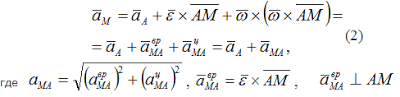
a^вр_MA= ε ⋅ AM - вращательное ускорение точки М при вращении вокруг точки А.

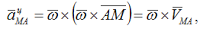
a^ц_MA= ω² ⋅ AM - центростремительное ускорение точки М при вращении вокруг точки А.

Центростремительное ускорение a^-ц_MA направлено от точки М к полюсу А.

Численную величину полного ускорения можно определить, спроецировав векторное равенство (2) на выбранные оси координат:

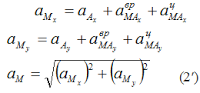
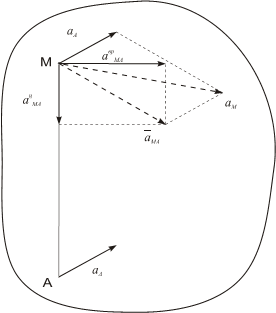
Рис. 1.11