Кинематика твердого тела. Обобщенные координаты. Парциальные движения. Теорема о скоростях точек твердого тела.

Задачи кинематики твердого тела

В кинематике твердого тела определяются закон движения и кинематические характеристики абсолютно твердого тела, а также кинематические характеристики точек тела.

Абсолютно твердым телом называется материальное тело, в котором расстояния между любыми двумя его точками остается постоянным.

Существуют две основные задачи кинематики твердого тела:

1. задание движения и определение кинематических характеристик движения тела;

2. определение кинематических характеристик движения (траектории, скорости и ускорения) отдельных точек тела.

Можно выделить пять видов движения твердого тела:

1. поступательное движение;

2. вращательное движение;

3. плоскопараллельное движение;

4. сферическое движение;

5. общий случай движения свободного твердого тела (сложное движение).

Обобщенные координаты

Обобщенные координаты – это независимые параметры однозначно определяющие положение механической системы в пространстве. Число обобщенных координат соответствует числу степеней свободы.

На рисунках 3.1, а; 3.1, б система имеет одну степень свободы, поэтому положение системы определяется одной обобщающей координатой s - на рисунке 3.1, а, φ- на рис. 3.1, б.

Обобщенные координаты могут иметь размерность длины (метр) или угла поворота (радиан).

На рисунке 3.1, в положение пластинки в плоскости может быть определено, если мы будем знать положение на этой плоскости какого-то отрезка, принадлежащего пластинке (например AB). А для этого нужно знать координаты какой-либо точки (например A) и угол наклона отрезка к какой-то оси, то есть в этом примере обобщенными координатами будут: x_A, y_A, φ.

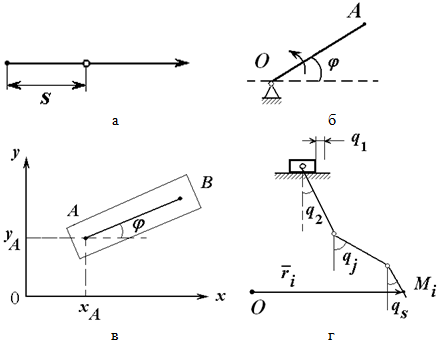
Рисунок 3.1

В теоретической механике принято обозначать обобщенные координаты символом q_j. Например (рисунок 3.1, г) для системы с s степенями свободы обобщенными координатами будут:

q₁, q₂ ... q_j ... q_s

т.е. параметры, с помощью которых можно определить положение любой точки механической системы:

r_i = r_i (q₁, q₂ ... q_j ... q_s).

Парциальные движения МО. Движение МО, при котором изменяется только одна из его обобщен- ных координат, а остальные неизменны, называется парциальным. По наличию или отсутствию парциальных движений проверяется не- зависимость величин, которые предполагается принять за обобщенные коор- динаты. Количеством парциальных движений определяется число степеней свободы МО, равное числу его обобщенных координат. Знание числа независимых координат, числа степеней свободы, совер- шенно необходимо для описания движения или покоя объекта. Ведь число независимых координат, уравнений движения или уравнений равновесия МО совпадает с его числом степеней свободы.

Теорема о проекциях скоростей двух точек тела

Определение скоростей точек плоской фигуры (или тела, дви­жущегося плоскопараллельно) связано обычно с довольно сложными расчетами. Однако можно получить ряд других, практически более удобных и простых мето­дов определения скоростей точек фигуры (или тела).

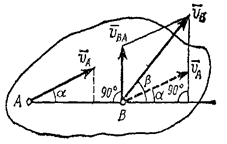
Рис.5

Один из таких методов дает тео­рема: проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу. Рассмотрим какие-нибудь две точки А и В плоской фигуры (или тела). Принимая точку А за полюс (рис.5), получаем 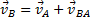. Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор 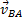перпендику­лярен АВ, находим

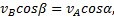
и теорема доказана.