Системы одновременных уравнений

Для изучения комплексных экономических явлений средствами эконометрики, как правило, применяют не отдельные уравнения регрессии, а системы уравнений.

Виды систем эконометрических уравнений:

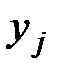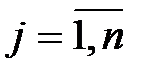1. Система независимых уравнений. Каждый результатив­ный признак (объясняемая переменная) , где , является функцией одной и той же сово­купности факторов (объясняющих пере­менных) 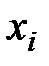, где 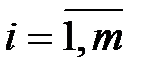. Набор факторов в каждом уравнении системы может варьировать в зависи­мости от изучаемого явления.

2. Система рекурсивных уравнений. Результативный признак 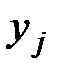, где 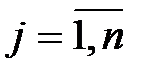, одного уравнения системы в каждом последующем уравнении является фактором наряду с одной и той же совокуп­ностью факторов 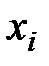, где .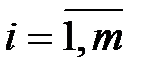

3. Система одновременных уравнений. Результативный признак 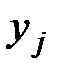, где 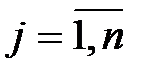одного уравнения системы входит во все другие уравне­ния системы в ка­честве фактора наряду с одной и той же совокупно­стью факторов 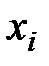, где 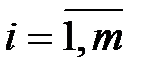. Такие системы эффективны в эконометрических исследованиях и наиболее широко применяются в макроэкономике.

Систему независимых или рекурсивных уравнений решают с помощью МНК. Для решения системы одновременных уравне­ний требуются другие, отличные от МНК методы.

Система одновременных уравнений может быть представлена:

1. В виде структурной формы модели.

2. В виде приведенной формы модели.

Основными составляющими обеих форм записи являются эн­догенные и экзогенные переменные. Эндогенные переменные (у)определяются внутри модели и являются зависимыми перемен­ными. Экзогенные переменные (х)определяются вне системы и являются независимыми переменными. Предполагается, что эк­зогенные переменные не коррелируют с ошибкой в соответству­ющем уравнении. Под предопределенной переменной системы одновременных уравнений понимают экзогенные и лаговые (за предыдущие мо­менты времени) эндогенные переменные этой системы.

Структурная форма модели имеет вид

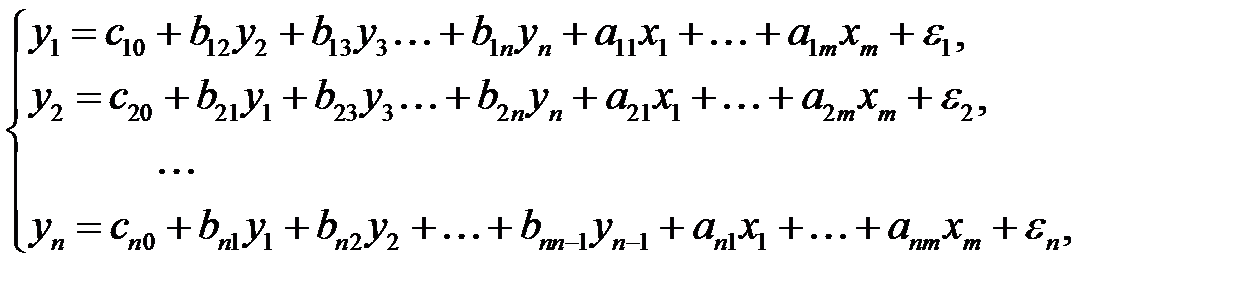
где 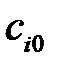, ( 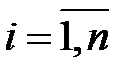) – свободный член уравнения модели, 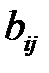, ( , 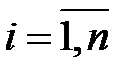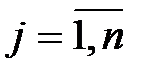) – коэффициент при эндогенной переменой модели, 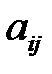, ( , 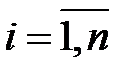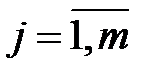) – коэффициент при экзогенной переменной, 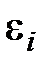, ( 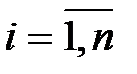)является случайной составляющей (ошибкой) 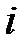-го уравнения структурной формы модели.

Наряду с регрессионными уравнениями в модели могут быть записаны и тождества. Таким образом, структурные уравнения модели подразделяются на два класса:

1. Поведенческие уравнения. Описывают взаимодействие между экзогенными и эндогенными переменными.

2. Тождества. Устанавливают соотношение между эндогенными перемен­ными, не содержат случайных составляющих и структурных коэффициентов модели.

Структурная форма модели может быть преобразована в при­веденную форму:

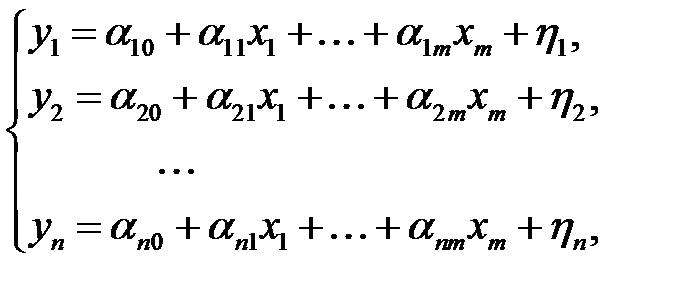
где 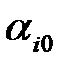, ( 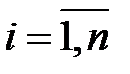) – свободный член уравнения модели, 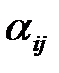, ( , 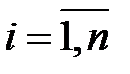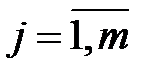) – коэффициент при предопределенной переменной является функцией коэффициентов структурной формы модели, 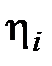, ( 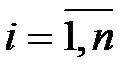) – случайная составляющая (ошибка) 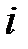-го уравнения приведенной формы модели.

Идентификация– это установление соответствия между приведенной и структурной формами модели. Единственность соответствия между приведенной и структурной формами модели составляет задачу идентификации.

Классы структурных моделей с точки зрения задачи идентификации:

1. Идентифицируемая. Все структурные коэффициенты однозначно определяются через приведенные коэффициенты.

2. Неидентифицируемая. Структурные коэффициенты невозможно найти по приведенным коэффициентам.

3. Сверхидентифиццруемая. Структурные коэффициенты, вы­раженные через приведенные коэффициенты, имеют два и более, числовых значений.

Необходимое условие идентифицируемости уравнений системы: Уравнение модели идентифицируемо, если количество эндогенных переменных (n) этого уравнения на единицу больше количества (р)предопределенных переменных системы, не входящих в данное уравнение: 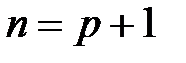. Если п < р + 1, то уравнение сверхидентифицируемо; если п> р + 1, то уравнение неидентифицируемо.

Достаточное условие идентифицируемости уравнений системы: Если определитель ( 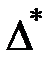) матрицы коэффициентов ( 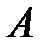)при переменных системы, не входящих в данное уравнение, не равен нулю и количество эндогенных переменных системы без единицы равно рангу этой матрицы, то уравнение модели идентифицируемо: , .

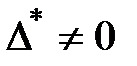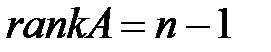Проверка структурной модели на идентифицируемость по­зволяет установить степень возможности оценки коэффициентов структурных уравнений по коэффициентам приведенных уравнений.

Пример 5.Проверить, идентифицируемы ли уравнения (1) и (2) модели предложения и спроса кейнсианского типа.

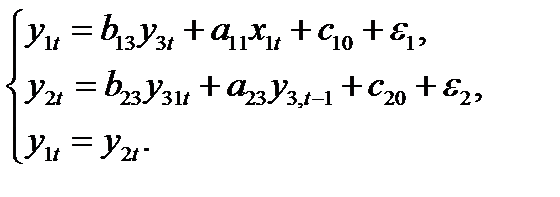
где 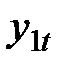– спрос на товар в момент времени ,

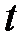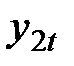– предложение товара в момент ,

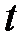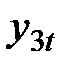– цена товара в момент ;

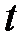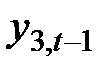– цена товара в момент ( 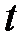– 1);

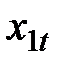– доход в момент ;

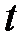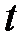– текущий период;

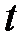( –1) – предыдущий период.

Решение.Запишем систему в виде

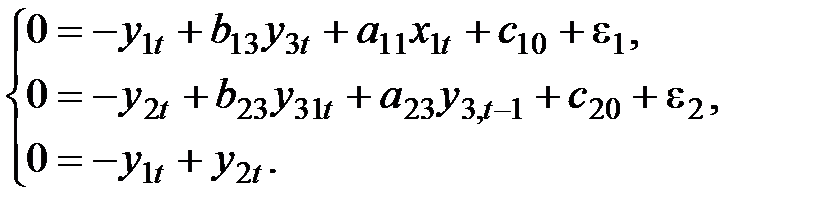
Запишем коэффициенты последней системы в виде следующей табл. 17:

Таблица 17

Уравнения	Переменные
эндогенные	предопределенные
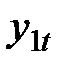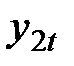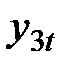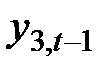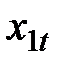(1)	-1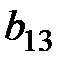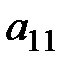
(2)		-1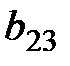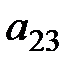
(3)	-1

Уравнение (1):

а) Необходимое условие: эндогенных переменных 2 ( 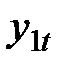, 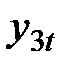), отсутствующих экзогенных – 1 ( 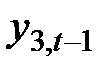). Таким образом, п = 2 , р = 1 и выполняется необходимое условие иденти­фикации: 2=1 + 1.

б) Достаточное условие. В первом уравнении отсутствуют 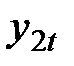и 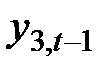. Запишем матрицу из коэффициентов при этих переменных в других уравнениях системы.

Уравнения	Переменные
эндогенные	предопределенные
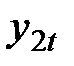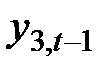(2)	-1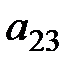
(3)

А – матрица коэффициентов при переменных системы, не входящих в уравнение. 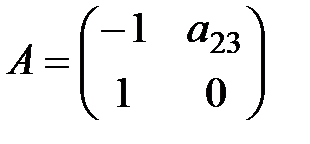. Ранг этой матрицы 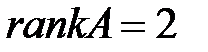(равен количеству эндогенных переменных модели минус один). Причем 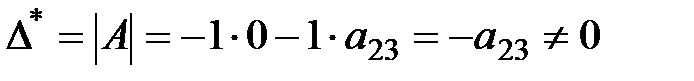. Достаточное условие идентифицируемости также выполняется. Можно сделать вывод о том, что уравнение (1) иден­тифицируемо.

Уравнение (2):

а) п = 2 , р = 1. Выполняется необходимое условие иденти­фикации: 2=1 + 1.

б) А– матрица коэффициентов при переменных системы, не входящих в уравнение. 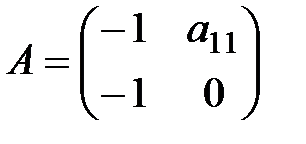Ранг этой матрицы 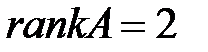(равен количеству эндогенных переменных модели минус один). Причем 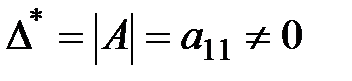. Достаточное условие идентифицируемости также вы­полняется. Можно сделать вывод о том, что уравнение (2) иден­тифицируемое.

Для получения качественных оценок параметров системы одновременных уравнений пользуются косвенным МНК:

1. Структурная форма модели преобразуется в приведенную форму.

2. С помощью МНК оцениваются параметры приведенной формы.

3. Приведенная форма преобразуется в структурную форму

Область применения косвенного МНК ограничивается идентифицируемыми системами одновременных уравнений.