Класс систем линейных уравнений
Класс для моделирования систем линейных уравнений назовем
SystemEq. Разместим его в модуле UnSystemEq.
// Файл UnSystemEq.h
#ifndef UnSystemEqH
#define UnSystemEqH
#include "UnMatrix.h"
// Класс систем уравнений получается множественным наследованием
// классов матриц и векторов
class SystemEq: public Matrix, public Vector
{
public:
SystemEq(int n = 1): Matrix(n, n), Vector(n) // Конструктор создает
{} // квадратную матрицу и вектор правой части
Vector SolveSystem(void); // Функция для решения системы уравнений
};
#endif
// Файл UnSystemEq.cpp
#include "SystemEq.h"
Vector SystemEq :: SolveSystem(void) // Решение системы уравнений
{
return ~(*this) * (Vector&)(*this);
}
Использованная в данной функции инструкция есть краткая запись следующей:
return operator~().operator*((Vector&)(*this));
Здесь видно, что сначала вызывается функция получения обратной матрицы, затем обратная матрица умножается на вектор правой части.
Приведение типа (Vector&)(*this) необходимо, чтобы разрешить неоднозначность между выбором одной из двух функций
Matrix :: operator*(const Matrix&) (умножение матрицы на матрицу) и
Matrix :: operator*(const Vector&) (умножение матрицы на вектор).
Пример использования классов
Разместим исходные данные в текстовом файле, например, InputData.txt. Первым элементом пусть будет порядок системы, далее пусть построчно располагаются элементы матрицы и, наконец, правая часть. Далее приведен вариант исходных данных:
1 2
3 4
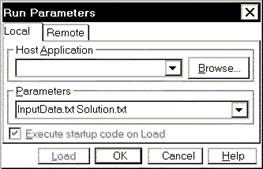
Рис. 48. Ввод параметров командной строки
Исходные данные следует прочитать из файла, решить систему уравнений и записать решение в файл. Имя исходного файла и файла решения будем задавать в командной строке программы. Аргументы командной строки можно указать непосредственно в среде C++Builder, выполнив команду меню Run, Parameters… . В появившемся окне (рис.48) в строке Parameters вводятся аргументы командной строки.
// Файл UnMainSolveSyst.cpp
#include <fstream.h>
#include <conio.h>
#include "UnMatrix.h"
#include "UnSystemEq.h"
#include "Rus.h"
int main(int argc, char* argv[])
{
if(argc < 3){ // Проверка наличия аргументов в командной строке
cout << Rus("Используйте командную строку\n"
"PrSolveSyst.exe ФайлИсходнДанных ФайлРешения");
getch();
exit(1);
}
ifstream istrm(argv[1]); // Поток для исходных данных
if(!istrm){ // Если произошла ошибка при открытии файла
cout << Rus("Не удалось открыть входной файл ") << argv[1];
getch();
exit(1);
}
int n; // Порядок системы
istrm >> n;
SystemEq S(n); // Создание системы уравнений
istrm >> (Matrix&) S; // Чтение матрицы системы
cout << Rus("Матрица системы \n"); // Вывод матрицы
cout << (Matrix&) S; getch(); // на экран
istrm >> (Vector&) S; // Чтение вектора правой части
cout << Rus("Правая часть системы \n"); // Вывод правой части
cout << (Vector&) S; getch(); // на экран
try{ // Попытка решить систему
Matrix A_1 = ~S; // Обратная матица системы
cout << Rus("Обратная матрица \n") << A_1; // Вывод обратной
getch(); // матрицы на экран
cout << Rus("Произведение матрицы на обратную \n") // Вычисление
<< (Matrix&)((Matrix &) S * A_1); // и вывод произведения
getch(); // исходной матрицы на обратную
Vector solution = S.SolveSystem(); // Решение системы
cout << Rus("Решение системы \n") << solution; // Вывод решения
getch();
ofstream ostrm(argv[2]); // Открытие выходного файла
if(!ostrm){ // Проверка открытия файла
cout << Rus("Не удалось открыть выходной файл ") << argv[2];
getch();
exit(1);
}
ostrm << solution; // Запись решения в файл
} // Конец блока try
catch(Matrix::MatrixException Exc){ // Обработчик исключений
cout << Exc.Mess; getch(); // Вывод сообщения об ошибке
}
return 0;
}
Если в нескольких базовых классах, которым наследует производный класс, есть функции с одинаковыми именами, все они становятся членами производного класса и компилятору надо давать дополнительные указания, какую именно функцию из нескольких одинаковых следует вызывать. Так, для умножения исходной матрицы на обратную будет неверно записать S * A_1, так как компилятор не cможет сделать выбор между двумя функциями Matrix::operator* и Vector::operator*, которые обе доступны для системы S, так как, с одной стороны система S – это матрица, а с другой стороны, – это вектор. Поэтому необходимо преобразование типа для выделения конкретной части производного класса: Matrix(S) или Vector(S), в зависимости от того, какую часть системы надо выделить – матрицу или вектор. При таком преобразовании вызываются конструкторы копирования соответствующих классов, которые создают временные объекты, используемые в вычислениях, что связано с определенными накладными расходами.
Если аргументы в функции передаются по ссылке, можно приводить производный объект к типу ссылки в виде (Matrix&)S или (Vector&)S, при этом конструкторы не вызываются и работа программы ускоряется.
Для открытия файловых потоков использованы конструкторы потоковых классов, аргументами которых являются имена файлов.
Программа выдает на экран:
Матрица системы
1 2
3 4
Правая часть системы
Обратная матрица
-2 1
1.5 -0.5
Произведение матрицы на обратную
1 0
8.88178e-16 1
Решение системы
0.5
Полученное решение будет также записано в файл, в данном примере – это Solution.txt.
Если задать вырожденную исходную матрицу, например,
1 2
3 6
появится сначала системное сообщение об ошибке, а затем, после нажатия F9 сообщение программы:
Матрица системы
1 2
3 6
Правая часть системы
Главный элемент = 0. Матрица вырожденная
Это результат работы нашего обработчика исключений. Системные сообщения об ошибках появляются только при запуске программы из среды разработки. При запуске программы независимо от среды будут выполняться только собственные обработчики исключений программы.
