Программа 48. многоугольники

В программе разработан класс Plgn для моделирования многоугольников на плоскости. В конструкторе этого класса динамически выделяется память под координаты вершин, а в деструкторе освобождается память, выделенная в конструкторе. В классе предусмотрены функции – члены для изображения многоугольника на экране, для его стирания с экрана, а также для перемещения и вращения многоугольника.

При решении задачи надо решить вопрос о совмещении математической плоскости, с помощью которой мы будем моделировать многоугольник, с физической плоскостью экрана. На рис.39 показана схема экрана и действующая на нем физическая экранная система координат xs, ys. Совместим начало математической системы координат x, y с центром экрана (x0, y0). Будем считать, что математическая плоскость отображается на плоскость экрана в масштабе 1:1, то есть математическая единица длины соответствует расстоянию между соседними пикселями на экране. Приведенные соображения реализованы в программе. В функциях рисования нужны физические координаты пикселей. Переход от математических координат к физическим производится по формулам:

xs = x0 + x, ys = y0 – y.

Знак минус учитывает разное направление вертикальных осей в физической и математической системах координат.

Рис.39. Плоскость экрана и математическая система координат

// Файл Polygon.cpp

class Plgn // Класс многоугольников

{

int n; // Число вершин

float *x; // Указатель на массив абсцисс

float *y; // Указатель на массив ординат

static int x0, y0; // Координаты центра экрана

public:

Plgn(int n = 3); // Конструктор с аргументом по умолчанию

~Plgn(); // Деструктор

void Show(); // Функция рисования многоугольника

void Hide(); // Функция, убирающая изображение

void Move(int dx, int dy); // Смещение многоугольника на dx, dy

void Rotate(float angle); // Поворот на угол angle градусов

void Movement(); // Движение, пока не нажата Esc

static void SetBegCoord(int xn, int yn) // Установка координат центра

{ x0 = xn; y0 = yn; }

};

# include <iostream.h>

# include <graphics.h> // Графика

# include <stdlib.h> // Доступ к random

# include <conio.h>

# include <math.h>

Plgn::Plgn(int nn) // Конструктор

{

n = nn;

x = new float [n]; // Выделение памяти под массив абсцисс

y = new float [n]; // Выделение памяти под массив ординат

for(int i = 0; i < n; i++){ // Заполнение массивов координат

x[i] = x0 - random(x0 * 2); // случайными числами

y[i] = y0 - random(y0 * 2);

}

}

Для простоты координаты вершин многоугольника задаются в конструкторе случайными числами с использованием функции

int random(int num);

которая генерирует случайное целое число из диапазона от 0 до num – 1; Таким образом, случайные координаты вершин многоугольника будут находиться в диапазонах [-x0, x0] и [-y0, y0] и, следовательно, не выйдут за пределы экрана.

Plgn::~Plgn() // Деструктор

{

delete [] x; // Освобождение

delete [] y; // памяти

}

void Plgn::Show() // Рисует многоугольник, рядом

{ // с вершиной выводит ее номер

char num[20]; // Память под номер вершины

for(int i = 0; i < n; i++){

line(x0 + x[i], y0 - y[i], // Изображение

x0 + x[(i + 1) % n], y0 - y[(i + 1) % n]); // i-й стороны

itoa(i, num, 10); // Получение номера вершины

outtextxy(x0 + x[i], y0 - y[i], num); // Вывод номера вершины

}

}

Функция line рисует отрезки, соединяющие соседние вершины. Возле вершин многоугольника выводятся их номера. Для вывода текста на экран в графическом режиме использована функция

void outtextxy(int x, int y, char *textstring);

которая выводит строку символов textstring, начиная с пикселя экрана с координатами x, y.

Для получения строки с номером вершины использована функция (заголовочный файл stdlib.h)

char *ltoa(long value, char *string, int radix);

которая преобразует число value в строку цифр string, дающую представление числа в системе счисления с основанием radix.

void Plgn::Hide() // Стереть изображение

{

int clr = getcolor(); // Запоминаем цвет рисования

setcolor(getbkcolor()); // Цветом рисования делаем цвет фона

Show(); // Рисуем цветом фона, изображение исчезает

setcolor(clr); // Восстанавливаем прежний цвет рисования

}

void Plgn::Move(int dx, int dy) // Смещение многоугольника на dx

{ // по горизонтали и на dy по вертикали

Hide(); // Убираем изображение

for(int i = 0; i < n; i++) // Смещение

x[i] += dx, y[i]+=dy; // каждой вершины

Show(); // Снова показываем многоугольник

}

Выпишем формулы, нужные для программирования поворота многоугольника вокруг центра масс. На рис.40 показан многоугольник и одна из его вершин M в исходном положении и после его поворота вокруг точки C на угол β. Новое положение вершины обозначено M₁.

В качестве центра масс можно взять точку C с координатами:

.

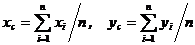Здесь n – число вершин многоугольника, x_i, y_i, i=1,…, n – координаты вершин. Данная формула действительно будет давать координаты центра масс, если вся масса многоугольника сосредоточена в его вершинах и массы вершин одинаковы.

Как видно из рис.40, координаты точки M относительно центра масс C равны:

.

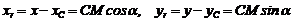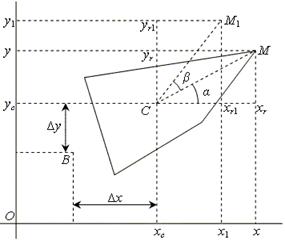
Рис.40. Поворот многоугольника вокруг центра масс

Так как 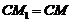, то относительные координаты точки M₁ после поворота выразятся формулами:

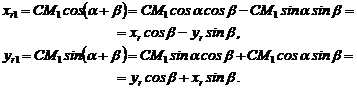
Таким образом, новые абсолютные координаты точки M будут:

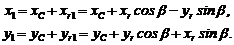
Эти формулы используются в функции вращения многоугольника:

void Plgn::Rotate(float angle) // Функция поворота многоугольника

{ // на угол angle (задается в градусах)

float xC = 0, yC = 0, xr, yr;

int i;

angle = angle*M_PI/180; // Перевод угла в радианы

Hide(); // Убираем изображение

for(i = 0; i < n; i++){ // Вычисление координат

xC += x[i]; yC += y[i]; // центра масс

}

xC /= n; yC /= n;

for(i = 0; i < n; i++){ // Получение координат вершин после поворота

xr = x[i] - xC; // Координаты вершины

yr = y[i] - yC; // относительно центра масс

x[i] = xC + xr * cos(angle) - yr * sin(angle); // Координаты вершины

y[i] = yC + xr * sin(angle) + yr * cos(angle); // после поворота

}

Show(); // Показываем многоугольник

}

void Plgn::Movement() // Движение при нажатии клавиш

{ // со стрелками, пока не нажата Esc

const int UP = 72, DOWN = 80, LFTUP = 76, // Константы

RIGHT = 77, LEFT = 75, ESC = 27; // для кодов клавиш

char c = 32; // Начальное значение для c должно отличаться от ESC

while(c != ESC){ // Пока не нажата клавиша esc

c = getch(); // Читаем код клавиши

if(c == 0) // Если у клавиши двухбайтовый код,

c = getch(); // читаем второй байт

switch(c){

case LEFT: Move(-1, 0); break; // Нажата стрелка влево

case RIGHT: Move(1, 0); break; // Нажата стрелка вправо

case UP: Move(0, 1); break; // Нажата стрелка вверх

case DOWN: Move(0, -1); break; // Нажата стрелка вниз

case LFTUP: Rotate(5); break;

}

}

}

Перемещение многоугольника производится нажатием клавиш со стрелками. Вращение – нажатием клавиши 5 на дополнительной цифровой клавиатуре. При этом не должна гореть лампочка NumLock, чтобы клавиши дополнительной цифровой клавиатуры работали как управляющие, а не как цифровые.

// Определение статических членов класса – координат центра экрана

int Plgn::x0, Plgn::y0;

void main()

{

int gd = DETECT, gmode, n, x;

char c;

randomize(); // Инициализация датчика случайных чисел

initgraph(&gd, &gmode, "C:\\TC30\\BGI"); // Установка граф. режима

// Задаем координаты центра экрана

Plgn::SetBegCoord(getmaxx() / 2, getmaxy() / 2);

cout << "Введите число вершин: ";

cin >> n; // Ввод числа вершин

Plgn mnog(n); // Многоугольник

setcolor(WHITE); // Установка цвета

mnog.Show(); // Вывод многоугольника

mnog.Movement(); // Перемещения многоугольника

mnog.Hide(); // Убираем многоугольник

Plgn triangle; // Многоугольник по умолчанию (треугольник)

triangle.Show(); // Показываем треугольник

triangle.Movement(); // Движение треугольника

triangle.Hide(); // Скрываем треугольник

closegraph(); // Переход в текстовый режим

}

Вызов статической функции

Plgn::SetBegCoord(getmaxx() / 2, getmaxy() / 2);

устанавливает для статических членов класса Plgn::x0, Plgn::y0 значения координат центра экрана.

В главной функции сначала создается многоугольник mnog, число вершин которого следует ввести. Затем для mnog вызывается функция Movement, которая позволяет его двигать и вращать. Далее создается треугольник triangle с использованием конструктора по умолчанию. Треугольником также можно «поиграть».

Для чтения кодов нажимаемых клавиш использована функция
int getch() (заголовочный файл conio.h), которая возвращает для обычных алфавитно-цифровых клавиш однобайтовый код, равный коду соответствующего символа, а для управляющих и функциональных клавиш – двухбайтовый код. Для таких клавиш при первом вызове getch() возвращает 0, а при втором – некоторый код, свой для каждой клавиши. Коды, возвращаемые getch(), можно узнать с помощью программы:

// Файл CodeKeys.cpp

// Получение кодов клавиш функцией getch()

#include <iostream.h>

#include <conio.h>

void main()

{

cout << "\nНажмите клавишу\n";

int c = getch();

if(0 == c){

c = getch();

cout << "\nУ клавиши двухбайтовый код: 0 " << c << endl;

}

else

cout << "\nУ клавиши однобайтовый код: " << c ;

getch();

}