Задачи 148-158. работа с экраном
Для доступа к функциям, работающим с экраном в текстовом режиме, следует включить в программу заголовочный файл conio.h. Основным инструментом для решения задач является функция window, создающая на экране окно.
148. Напишите функцию void border_win(int x1, int y1, int x2, int y2), создающую на экране текстовое окно, окаймленное рамкой из двойных линий. Указание. Рамки можно рисовать, выводя функцией putch символы псевдографики. Для этих символов нет клавиш, поэтому их вводят в текст программы с помощью кода: удерживая клавишу Alt, набирают десятичный код символа на дополнительной цифровой клавиатуре, расположенной справа. Символы для рисования двойных и одинарных линий и их коды приведены в табл.19.
Таблица 19. Символы псевдографики и их коды
| Символ | '║' | '╗' | '╝' | '╚' | '╔' | '═' | '│' | '┐' | '└' | '─' | '┘' | '┌' |
| Код |
149. Напишите функцию void border_win(int x1, int y1, int x2, int y2), создающую на экране текстовое окно, окаймленное рамкой из одинарных линий.
150. Напишите программу, изображающую на экране флаг Франции. Цвета французского флага, как у российского, но полосы идут вертикально.
151. Напишите программу, изображающую на экране шахматную доску. Предусмотрите возможность использования различных цветов для изображения полей доски.
152. Напишите программу, которая перемещает курсор по экрану на одну позицию влево при нажатии клавиши "стрелка влево" ß и вправо, при нажатии клавиши "стрелка вправо" à. Программа должна прекращать работу при нажатии любой другой клавиши.
153. Напишите программу, которая устанавливала бы курсор в крайнее правое положение на экране при нажатии клавиши End и в крайнее левое положение при нажатии клавиши Home, и завершала работу при нажатии любой другой клавиши.
При написании программ для задач из данного раздела не забывайте включить в программу заголовочный файл graphics.h и правильно вызвать функцию initgraph для инициализации графического режима.
154. Напишите программу, изображающую на экране замкнутый многоугольник. Входными данными должны быть число вершин и координаты вершин.
155. Напишите программу, которая рисует на экране правильный n-угольник и описанную вокруг него окружность.
156. Напишите программу, которая рисует на экране правильный n-угольники вписанную в него окружность.
157. Напишите программу, изображающую на экране график функции sin(x).
158. Напишите функцию, которая рисует на экране график некоторой математической функции с одним аргументом. Функция рисования графика должна получать в качестве аргумента указатель на функцию для вычисления значений математической функции, границы отрезка и число точек по которым строится график.
Глава 13. Внутреннее представление чисел
Двоичная система счисления
Числа, символы, изображения, звуки кодируются в компьютерах в виде последовательностей битов, которые могут находиться в двух различных состояниях. Эти состояния удобно описывать двумя значениями 0 и 1 и считать цифрами, а последовательности этих цифр рассматривать как числа, представленные в двоичной системе счисления. Числа в двоичной системе счисления, так же, как и в десятичной, представляются последовательностью цифр (нулей и единиц), имеющих различный «вес», определяемый положением цифры в числе. В десятичной системе в качестве «веса» цифры используется степень 10, а в двоичной – степень 2. Вес или старшинство цифры возрастает справа налево. В этом же направлении нумеруются разряды, причем нумерация начинается с 0. В табл.20 показаны цифры двоичного числа 01001110 и веса его цифр.
Таблица 20. Веса двоичных цифр
| Номер разряда | ||||||||
| Цифра | ||||||||
| Вес цифры | 27=128 | 26=64 | 25=32 | 24=16 | 23=8 | 22=4 | 21=2 | 20=1 |
Для получения значения числа в десятичной системе следует умножить веса на значения цифр и сложить:
01001110 = 0×128 + 1×64 + 0×32 + 0×16 + 1×8 + 1×4 + 1×2 + 0×1 = 78.
Двоичные цифры числа получаются путем последовательного деления числа на 2 и нахождения остатков от деления, табл.21.
Таблица 21. Получение двоичных цифр
| Частное | 78/2 = 39 | 39/2 = 19 | 19/2 = 9 | 9/2 = 4 | 4/2 = 2 | 2/2 = 1 | 1 / 2 = 0 |
| Остаток | 78%2 = 0 | 39%2 = 1 | 19%2 = 1 | 9%2 = 1 | 4%2 = 0 | 2%2 = 0 | 1%2 = 1 |
| Цифра |
Деление числа производится до тех пор, пока не получится нуль. Цифры выписываются в обратном порядке.
Беззнаковые целые
Беззнаковые целые типы имеют неотрицательные значения. Рассмотрим в качестве примера внутреннее представление типа
unsigned char, представление остальных беззнаковых типов
(unsigned short, unsigned int, unsigned long) аналогично. Под данные типа unsigned char отводится 1 байт памяти, состоящий из 8 битов или разрядов. Эти разряды могут образовывать
28 = 256
различных комбинаций из нулей и единиц:
00000000, 00000001, …, 11111111.
Данные комбинации рассматриваются как двоичные числа со значениями:
0, 1, 2, …, 255.
Наибольшее значение 255 равно:
28 – 1.
В общем случае, если n – количество двоичных разрядов, отводимых для беззнакового типа, то наибольшее значение этого типа равно:
2n – 1.
При вычислениях с беззнаковыми целыми используется арифметика по модулю 2n, то есть в качестве результата любой операции берется остаток от деления на 2n, который может иметь значения от 0 до 2n – 1, поэтому при вычислениях не может быть переполнения.
Рассмотрим сложение двух чисел 100 и 200 типа unsigned char. Найдем их двоичное представление в виде 8 двоичных цифр, рис.31, 32.
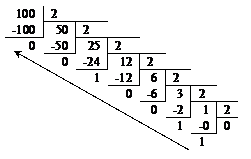
10010 = 011001002
Рис.31. Получение двоичного представления для числа 100
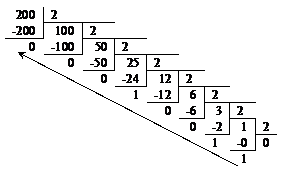
20010 = 110010002
Рис.32. Получение двоичного представления для числа 200
Обратим внимание, что двоичное представление для 200 получается из двоичного представления для 100 путем сдвига всех его разрядов влево на 1 позицию.
Выполним сложение этих числе столбиком:
| + | ||||||||
Для старшей единицы не хватает разряда, поэтому она отбрасывается, в результате получаем:
10010 + 20010 = 001011002 = 32+8+4 = 4410.
Найдем теперь разность 100 - 200:
| – | ||||||||
Здесь выполняется заем из несуществующего девятого разряда, в результате получается:
10010 – 20010 = 100111002 = 128 + 16 + 8 + 4 = 15610.
Двоичный дополнительный код
Рассмотрим теперь знаковый тип char. Здесь часть битовых комбинаций рассматриваются как положительные числа, а часть как отрицательные. В качестве нуля и положительных чисел принимаются битовые комбинации:
00000000, 00000001,…, 01111111.
Эти комбинации рассматриваются как числа в двоичной системе счисления со значениями:
0, 1, 2, …, 127.
Для отрицательных чисел остаются комбинации:
10000000. 10000001, 10000010, …, 11111111,
у которых старший разряд равен 1. Данным комбинациям можно поставить в соответствие отрицательные числа различными способами. Наиболее удобным оказался дополнительный код, показанный в табл.22.
Таблица 22. Двоичный дополнительный код
| Битовая комбинация | Числовое значение | Битовая комбинация | Числовое значение |
| 1000 0000 | –128 | ||
| 0111 1111 | 1000 0001 | –127 | |
| 0111 1110 | 1000 0010 | –126 | |
| … | … | … | … |
| 0000 0111 | 1111 1001 | -7 | |
| 0000 0110 | 1111 1010 | –6 | |
| 0000 0101 | 1111 1011 | –5 | |
| 0000 0100 | 1111 1100 | –4 | |
| 0000 0011 | 1111 1101 | –3 | |
| 0000 0010 | 1111 1110 | –2 | |
| 0000 0001 | 1111 1111 | –1 | |
| 0000 0000 |
Сравнивая комбинации для положительных и отрицательных чисел, замечаем, что старшие разряды одинаковых по модулю чисел являются обратными или дополнительными по отношению друг к другу, то есть 0 заменяется 1 и наоборот, младшие же разряды одинаковы. Отсюда вытекает следующее правило:
для получения представления абсолютного значения какого-либо отрицательного числа нужно выписать разряды справа, включая первую 1, а все разряды после первой 1 заменить на обратные; для получения представления какого-либо отрицательного числа нужно выписывать разряды для его модуля вплоть до первой 1, а остальные разряды заменить на обратные.
Можно сформулировать и другое правило:
для нахождения модуля отрицательного числа, представленного в двоичном дополнительном коде, нужно заменить все его разряды на обратные и добавить 1.
Найдем, для примера, сумму 1 + (–1):
| + | ||||||||
Девятый разряд выходит за границы разрядной сетки и отбрасывается, поэтому получается правильный результат 0.
Формально результат сложения
1 + (–1)
равен
1000000002 = 28.
Такой же результат получается при сложении любых двух одинаковых по модулю чисел противоположного знака, то есть битовые комбинации противоположных по знаку чисел дополняют друг друга до 28. Отсюда произошло название данного способа представления чисел.
Преимущество двоичного дополнительного кода состоит в том, что процессору достаточно уметь выполнять только две операции: сложения и получения обратного по знаку числа, вычитание сводится к этим операциям, так как разность любых чисел a – b можно представить в виде суммы a + (-b).
Ограниченность разрядной сетки приводит в предельных случаях к парадоксальным результатам. Вычислим, например, 127 + 1:
| + | ||||||||
Получили:
127 + 1 = –128.
Другие знаковые типы используют также двоичный дополнительный код, только имеют большее число разрядов.
Двоичный код с избытком
В некоторых случаях для отрицательных чисел используется другое представление, называемое двоичным кодом с избытком, табл.23.
Здесь битовые комбинации и соответствующие им числа расположены по возрастанию, нуль занимает центральное положение. Если рассматривать битовые комбинации просто как двоичные числа, то для получения соответствующего числового значения нужно из двоичного числа вычесть 128. Можно сказать и по-другому: числа хранятся в виде, увеличенном на 128, отсюда и происходит название данного представления: код с избытком.
Двоичная нотация с избытком применяется для хранения порядка чисел с плавающей точкой.
Таблица 23. Код с избытком 128
| Битовая комбинация | Числовое значение |
| 1111 1111 | |
| 1111 1110 | |
| … | … |
| 1000 0011 | |
| 1000 0010 | |
| 1000 0001 | |
| 1000 0000 | |
| 0111 1111 | –1 |
| 0111 1110 | –2 |
| 0111 1101 | –3 |
| … | … |
| 0000 0001 | –127 |
| 0000 0000 | –128 |
Побитовые операторы
Побитовые операторы применимы только к целым типам. Они действуют на отдельные разряды двоичного представления чисел. Напомним, что имеются следующие побитовые операторы:
| – побитовое логическое ИЛИ,
& – побитовое логическое И,
^ – побитовое исключающее ИЛИ,
~ – побитовое логическое отрицание,
<< – сдвиг влево,
>> – сдвиг вправо.
В табл.24 представлены результаты выполнения побитовых операторов над двумя битами a и b.
Таблица 24. Таблица истинности побитовых
логических операторов
| a | b | a|b | a&b | a^b | ~a |
Оператор побитового ИЛИ можно использовать для установки в 1 заданных разрядов числа, например, после выполнения инструкции
y = x | 017;
четыре младших разряда y будут равны 1. Действительно, пусть x, y занимают 1 байт памяти и x имеет исходное значение
x7x6x5x4 x3x2x1x0,
тогда
| x: | | | x7 | x6 | x5 | x4 | x3 | x2 | x1 | x0 |
| 017: | |||||||||
| y= | x7 | x6 | x5 | x4 |
Оператор побитового И можно использовать для установки в 0 заданных разрядов числа, например, после выполнения инструкции
y = x & 017;
четыре старших разряда y будут нулями, а младшие разряды не изменятся. Пусть, например, x имеет исходное значение:
x7x6x5x4 x3x2x1x0,
тогда
| x: | & | x7 | x6 | x5 | x4 | x3 | x2 | x1 | x0 |
| 017: | |||||||||
| y= | x3 | x2 | x1 | x0 |
Оператор побитового исключающего ИЛИ можно использовать для изменения заданных разрядов на противоположные. Например, пусть переменная x имеет исходное значение:
1100 0101.
Найдем его значение после выполнения инструкции:
x = x ^ 017;
| x: | ^ | ||||||||
| 017: | |||||||||
| x=x^017: |
Видно, что младшие разряды x приняли противоположное значение, а старшие не изменились.
Оператор ~ инвертирует (меняет на противоположные) все биты операнда. Пусть, например, x имеет код:
1100 0101.
После выполнения инструкции y = ~x; двоичный код для y будет:
0011 1010.
Операторы << и >> сдвигают свои первые операнды соответственно влево и вправо на число позиций, заданных вторым операндом. Значение второго операнда этих операторов должно быть неотрицательным.
Так,
y << 2
сдвигает значение y влево на 2 разряда, заполняя освобождающиеся разряды нулями, что, кстати, эквивалентно умножению на 4. Если y имеет тип char и двоичное представление
1100 01012 = –0011 10112 = –5910,
то выражение y << 2 имеет значение:
1100 0101 << 2 = 0001 01002 = 2010.
Умножим теперь -59 на 4, что эквивалентно четырехкратному сложению:
| + + + | ||||||||
Как видим, результат одинаков.
При сдвиге вправо беззнаковой величины освобождающиеся разряды заполняются нулями.
При сдвиге вправо знаковой величины происходит «размножение» знака, благодаря чему отрицательное число остается отрицательным после сдвига, а положительное – положительным
Сдвиг вправо на один разряд эквивалентен делению числа на 2. Пусть y имеет рассмотренное выше значение
1100 01012 = -5910.
Значение выражения y >> 2 равно
(1100 0101 >> 2) = 111100 012 = -0000 11112 = -15.
Это эквивалентно делению на 4 с отбрасыванием остатка.
