Программа 19. Аргументы по умолчанию

Функция печати целого print рекурсивная. Если основание системы счисления base <= 10, используются обычные цифры 0, 1, …, 9. Если base > 10, то в качестве цифр используются заглавные латинские буквы A, B, C, D, E, F, G, H,… со значениями: 10, 11, 12, 13, 14, 15, 16, 17,…

// Файл ArgDeflt.cpp

#include <iostream.h>

#include <conio.h>

// print: печать val в системе счисления с основанием base

void print(int val, int base = 10) // 10 – значение для base по умолчанию

{

if(val < 0){

cout.put('-');

print(-val, base);

}

if(val / base > 0) // Если число многозначное,

print(val / base, base); // печатать старшие цифры

int r = val % base; // Остаток от деления

if(r < 10)

cout.put('0' + r);

else

cout.put('A' + r - 10);

}

void main()

{

print(31); cout.put(' '); // По умолчанию base = 10

print(31, 10); cout.put(' ');

print(31, 16); cout.put(' ');

print(31, 2); cout.put('\n');

getch();

}

Программа печатает:

31 31 1F 11111

Для формирования цифр, значения которых больше 9, в функции print использовано выражение:

'A' + r – 10.

Для val = 31 и base = 16 значение остатка r = 31 % 16 = 15. Поэтому

'A' + r – 10 = 'A' + 15 – 10 = 'F'.

Аргументы по умолчанию можно задавать только в конце списка аргументов, например,

int f(int, int = 0, char = 0); // Правильно

int g(int = 0, int = 0, char); // Ошибка

Задачи 70-96. Функции

В приводимых ниже задачах надо написать полностью законченную программу, включающую функцию main, которая должна вызывать функцию, о которой речь идет в задаче.

70. В задаче 14 приведена формула для величины ежемесячных выплат по кредиту. Напишите функцию, возвращающую в качестве результата величину x. Используя эту функцию, напечатайте таблицу значений выплат x в зависимости от количества месяцев N при некоторой фиксированной величине кредита P и процентной ставке r.

71. Напишите функцию, возвращающую номер первого элемента массива v, совпадающего с x. Если совпадений нет – возвратить -1.

72. Напишите функцию, возвращающую номер последнего элемента массива v, совпадающего с x, или -1, если совпадений нет.

73. Напишите функцию, возвращающую число совпадений x с элементами массива v.

74. Напишите функцию для нахождения среднего арифметического значения m элементов массива x[] с элементами вещественного типа и функцию для вычисления среднего квадратичного отклонения σ. Формулы следующие:

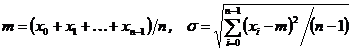
75. Напишите функцию, аргументом которой является номер года. Функция должна возвращать 1, если год високосный и 0, если год невисокосный. Год является високосным, если его номер делится на 4 и не делится на 100 или делится на 400. В соответствии с этим правилом 1900-й год был невисокосным, а 2000-й – високосным.

76. Напишите функцию lower, преобразующую латинские буквы верхнего регистра (заглавные) в латинские буквы нижнего регистра (строчные). Символ, не являющийся буквой, должен возвращаться без изменения. Указание. Используйте тот факт, что как заглавные, так и строчные буквы в кодовой таблице расположены плотно, без разрывов, поэтому разница между кодами одноименных символов одинакова и равна 'a' - 'A'.

77. Случайные целые числа в диапазоне от-32768 до 32767 можно получить с помощью следующей функции

int casual() // rand: получение псевдослучайных чисел

{ // в диапазоне от -32768 до 32767

static int randx = 1; // Статическая переменная сохраняет свое

// значение между вызовами функции

randx = (randx * 25173 + 13849) % 65536;

return randx;

}

Используя функцию casual(),заполните случайными числами двухмерный массив (квадратную матрицу) размером N * N, где N определите как целую положительную константу. Получите два массива (вектора): вектор, элементы которого равны средним арифметическим значениям строк матрицы, и вектор, элементы которого равны средним арифметическим значениям столбцов матрицы.

78. Решите предыдущую задачу с использованием библиотечной функции rand, заголовочный файл stdlib.h.

79. Пусть имеется упорядоченный по возрастанию массив x. Напишите функцию, возвращающую номер элемента массива, имеющего заданное значение y или -1, если такого элемента нет. Используйте метод двоичного (бинарного) поиска: y сравнивается со средним элементом массива; если числа равны, поиск завершается, если y меньше среднего элемента, то y надо искать в левой половине, а иначе – в правой; к выбранной половине применяется тот же алгоритм.

80. Напишите функцию для вычисления определителя третьего порядка.

81. Напишите функцию для решения системы линейных уравнений третьего порядка по правилу Крамера.

82. Напишите функцию вычисления определителя четвертого порядка путем разложения определителя по элементам некоторой строки.

83. Напишите функцию вычисления определителя четвертого порядка используя разложение определителя по элементам некоторого столбца.

84. Напишите функцию для решения системы линейных уравнений четвертого порядка по правилу Крамера.

85. Пусть даны матрица a порядка n и n-мерный вектор b. Напишите функцию, заменяющую заданный столбец матрицы a на вектор b.

86. Напишите функцию для вычисления обратной матрицы третьего порядка.

87. Напишите функцию, осуществляющую умножение двух квадратных матриц.

88. Напишите функцию для вычисления обратной матрицы четвертого порядка.

89. Напишите функцию, приводящую квадратную матрицу к треугольному виду методом Гаусса. Функция должна возвращать true при успешном выполнении приведения и false, если в процессе приведения встретилось деление на нуль.

90. Напишите рекурсивную функцию вычисления факториала n!.

91. Напишите рекурсивную функцию вычисления числа Фибоначчи с заданным номером. Числа Фибоначчи определяются формулами:

f₀ = f₁ = 1; f_n =f_n-1 + f_n-2 при n = 2, 3,…

92. Напишите рекурсивную функцию вычисления целой степени целого числа.

93. Напишите рекурсивную функцию вычисления целой степени вещественного числа.

94. Напишите рекурсивную функцию нахождения наибольшего общего делителя NOD(m, n) двух целых m, n по алгоритму Эвклида:

пусть m > n, тогда, если n = 0то NOD(m, n) = m,

если же n > 0, то NOD(m, n) = NOD(m, m – n).

Кроме того, NOD(m, n) = NOD(n, m).

95. Напишите рекурсивную функцию для нахождения биномиальных коэффициентов, пользуясь их определением:

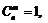если m = 0, n > 0 или m = n³ 0;

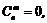если m > n ³ 0;

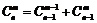в остальных случаях.

96. Напишите рекурсивную функцию вычисления длины строки.

Глава 8. Символы и строки

Символы

Для работы с символами в языке C++ используется тип char. Как уже говорилось, это целый тип, с небольшим диапазоном значений, который можно использовать везде, где допустимо использовать целые.

Символьные константы

В тексте программ могут использоваться символьные константы, заключаемые в одиночные апострофы, например ’g’, ’F’, ’Q’ – латинские буквы, ’Ц’, ’г’, ’ж’ – русские буквы, ’0’, ’1’, ’9’ – цифры, ’.’, ’,’, ’:’ – знаки препинания. Эти константы имеют тип char, а их числовые значения равны кодам символов в кодовой таблице. Символьные константы могут использоваться в любых выражениях, где допустимо вхождение других целых типов.

Так как под тип char отводится один байт памяти, всего существует 256 символов. На клавиатуре компьютера есть клавиши только для части символов, входящих в кодовую таблицу, на экране же дисплея можно показать большинство символов, так как изображение создается из отдельных точек. Символы, генерируемые клавишами Backspace, Tab, Esc и некоторыми другими не имеют изображения, так как за этими символами закреплены определенные действия, например, вывод на экран символа «табуляция» приводит к перемещению курсора в следующую позицию табуляции. Ряд символов в языке C++ имеют служебное назначение, например, «двойная кавычка», «апостроф», «обратная наклонная черта».

Таблица 13. Представление символов

Обозначение	Название символа	Обозначение	Название символа
\a \b \f \n \r \ooo \xhh	сигнал звонок возврат на шаг перевод страницы новая строка возврат каретки восьмеричный код шестнадцатеричный код	\\ \? \' \” \v \t	обратная наклонная черта знак вопроса апостроф двойная кавычка вертикальная табуляция горизонтальная табуляция

Служебные символы и символы, у которых нет графического образа, имеют в C++ специальное представление, иногда называемое эскейп-последовательностью. Данное представление начинается с обратной наклонной черты (\). Символы, представляемые эскейп-последовательностями, перечислены в табл.13. В таблице обозначено: ooo – одна, две или три восьмеричные цифры, hh – одна или две шестнадцатеричные цифры. Данные комбинации цифр должны представлять код символа в кодовой таблице.

Компилятор, встретив в тексте программы указанные последовательности, рассматривает их как один соответствующий символ.

При выводе значений типа char оператор << создает на экране изображение соответствующего символа. При необходимости вывести код символа, его следует преобразовать к типу int с помощью конструкции:

int(выр),

где выр – выражение типа char, которое преобразуется к целому типу. Сказанное иллюстрируется приводимой далее программой.