Геометрическое и аналитическое условия равновесия сходящихся сил. Равновесие трех непараллельных сил.
1. Геометрическое условие равновесия. Так как главный вектор R системы сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил (см. рис. 15), то R может обратиться в нуль только тогда, когда конец последней силы в многоугольнике совпадает с началом первой силы, т. е. когда многоугольник замкнется.
Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым.
2. Аналитические условия равновесия. Аналитически модуль главного вектора системы сил определяется формулой
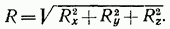
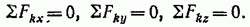
Равенства (11) выражают условия равновесия в аналитической форме: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы, суммы проекций этих сил на каждую из трех координатных осей были равны нулю.
Если все действующие на тело сходящиеся силы лежат в одной плоскости, то они образуют плоскую систему сходящихся сил. В случае плоской системы сходящихся сил получим, очевидно, только два условия равновесия:
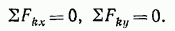
3. Теорема о трех силах. Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
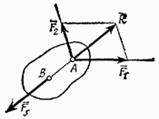 Для доказательства теоремы рассмотрим сначала какие-нибудь две из действующих на тело сил, например
Для доказательства теоремы рассмотрим сначала какие-нибудь две из действующих на тело сил, например  Так как по условиям теоремы эти силы лежат в одной плоскости и не параллельны, то их линии действия пересекаются в некоторой точке А (рис. 22). Приложим силы
Так как по условиям теоремы эти силы лежат в одной плоскости и не параллельны, то их линии действия пересекаются в некоторой точке А (рис. 22). Приложим силы  в этой точке и заменим их равнодействующей R. Тогда на тело будут действовать две силы: сила R и сила
в этой точке и заменим их равнодействующей R. Тогда на тело будут действовать две силы: сила R и сила  приложенная в какой-то точке В тела. Если тело при этом находится в равновесии, то силы R и
приложенная в какой-то точке В тела. Если тело при этом находится в равновесии, то силы R и  должны быть направлены по одной прямой, т. е. вдоль АВ. Следовательно, линия действия силы F, тоже проходит через точку А, что и требовалось доказать.
должны быть направлены по одной прямой, т. е. вдоль АВ. Следовательно, линия действия силы F, тоже проходит через точку А, что и требовалось доказать.
Обратная теорема места не имеет, т. е. если линии действия трех сил пересекаются в одной точке, то тело под действием этих сил может и не находиться в равновесии; следовательно, теорема выражает только необходимое условие равновесия тела под действием трек сил.
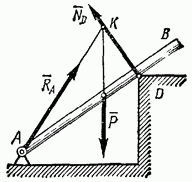
Рис. 23
Пример. Рассмотрим брус АВ, закрепленный в точке А шарниром и опирающийся на выступ D (рис. 23). На этот брус действуют три силы - сила тяжести  реакция
реакция  выступа и реакция RA шарнира. Так как брус находится в равновесии, то линии действия этих
выступа и реакция RA шарнира. Так как брус находится в равновесии, то линии действия этих  должны пересекаться в одной точке. Линии действия сил Р и
должны пересекаться в одной точке. Линии действия сил Р и  известны и они пересекаются в точке К. Следовательно, линия действия приложенной в точке А реакции RA тоже должна пройти через точку
известны и они пересекаются в точке К. Следовательно, линия действия приложенной в точке А реакции RA тоже должна пройти через точку  , т. е. должна быть направлена вдоль прямой АК. Теорема о трех силах позволила в этом случае определить заранее неизвестное направление реакции шарнира А.
, т. е. должна быть направлена вдоль прямой АК. Теорема о трех силах позволила в этом случае определить заранее неизвестное направление реакции шарнира А.
5)Алгебраический и векторный моменты силы 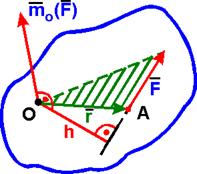 относительно центра
относительно центра
Моментом силы F относительно центра (точки) О называется вектор mo(F) равный векторному произведению радиуса вектора r, проведенного из центра О в точку А приложения силы, на вектор силы F:
| mo(F) = rx F. |
Вектор mo(F) приложен в точке О инаправлен ^ плоскости, проходящей через центр О и силу F, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки.
Модуль mo(F) равен произведению модуля силы F на плечо h:
| | mo(F)| = F*h, |
где плечо h - перпендикуляр, опущенный из центра О на линию действия силы F.
Момент mo(F) характеризует вращательный эффект силы F относительно центра (точки) О.
Свойства момента силы:
1. Момент силы относительно центра не изменяется при переносе силы вдоль линии ее действия в любую точку;
2. Еслилиния действия силы проходит через центр О (h = 0), то момент силы относительно центра О равен нулю.
Для плоской системы сил при вычислении моментов сил относительно точки (центра), находящейся в той же плоскости, пользуются понятием алгебраического момента силы относительно точки.
Алгебраический момент силы F относительно точки О равен взятому с соответствующим знаком произведению модуля силы на ее плечо:
| mo(F) = ± F*h. |
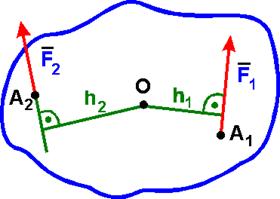 Момент считается положительным, если сила стремится повернуть тело вокруг точки О против хода часовой стрелки, и отрицательным - по ходу часовой стрелки:
Момент считается положительным, если сила стремится повернуть тело вокруг точки О против хода часовой стрелки, и отрицательным - по ходу часовой стрелки:
| mo(F2) = - F2*h2. |
При определении алгебраического момента силы относительно точки в случае, когда сложно найти плечо h, следует разложить силу на составляющие, параллельные осям координат, и применить теорему Вариньона: если данная система сил имеет равнодействующую, то момент равнодействующей относительно любой точки О равен сумме моментов составляющих сил, относительно той же точки, т. е.
| mo(R) = Smo(Fk), (k = 1, 2, .., n) |
где R = S(Fk) (k = 1, 2, .., n).
Например: F = F¢ + F², где F¢ = F×cosa, F² = F×sina
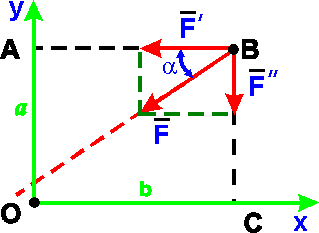
По теореме Вариньона
| mo(F) = mo(F¢) + mo(F²) = F¢×ОА - F²×ОС = = F×cosa×a-F×sina×b. |
