Система сходящихся сил. Геометрический и аналитический способы сложения сил. Равнодействующая сходящихся сил.

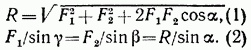
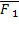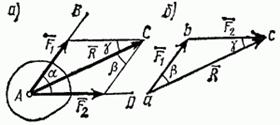
1. Сложение двух сил. Геометрическая сумма R двух сил и 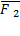находится по правилу параллелограмма (рис. 13, а) или построением силового треугольника (рис. 13, б), изображающего одну из половин этого параллелограмма. Если угол между силами равен α, то модуль R и углы β, γ, которые сила R образует со слагаемыми силами, определяются по формулам:

Рис. 13

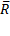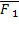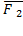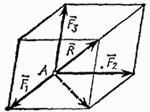
2. Сложение трех сил, не лежащих в одной плоскости. Геометрическая сумма трех сил , , 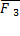не лежащих в одной плоскости, изображается диагональю параллелепипеда, построенного на этих силах (правило параллелепипеда). В справедливости этого убеждаемся, применяя последовательно правило параллелограмма (рис. 14).

3. Сложение системы сил. Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил 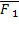, , 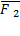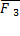... 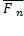(рис. 15, а) откладываем от произвольной точки О (рис. 15, б) вектор 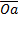изображающий в выбранном масштабе силу 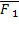от точки а — вектор 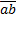изображающий силу 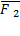от точки b — вектор 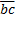изображающий силу 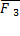и т.д.; от конца m предпоследнего вектора откладываем вектор изображающий силу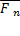

Соединяя начало первого вектора с концом последнего, получаем вектор 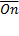= 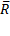изображающий геометрическую сумму или главный вектор слагаемых сил:

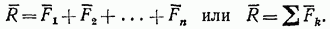
4. Равнодействующая сходящихся сил. Рассмотрим систему сходящихся сил, т. е. сил, линии действия которых пересекаются в одной точке (рис. 15, а). Так как сила, действующая на абсолютно твердое тело, является вектором скользящим, то система сходящихся сил эквивалентна системе сил, приложенных в одной точке (на рис. 15, а в точке А).

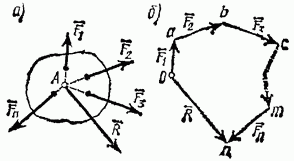
Рис. 15

Последовательно применяя закон параллелограмма сил, придем к выводу, что система сходящихся сил имеет равнодействующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке пересечения их линий действия. Следовательно система сил 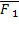, , 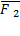... 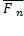изображенных на рис. 15, а, имеет равнодействующую, равную их главному вектору R и приложенную в точке А (или в любой другой точке, лежащей на линии действия силы R, проведенной через точку А).

5. Разложение сил. Разложить данную силу на несколько составляющих — значит найти такую систему нескольких сил, для которой данная сила является равнодействующей. Эта задача является неопределенной и имеет однозначное решение лишь при задании дополнительных условий. Рассмотрим два частных случая:

а) разложение силы по двум заданным направлениям. Задача сводится к построению такого параллелограмма, у которого разлагаемая сила является диагональю, а стороны параллельны заданным направлениям. Например, на рис. 13 показано, как сила R разлагается по направлениям АВ и AD на силы 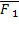и 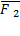- составляющие силы R (сила R и прямые АВ, AD лежат, конечно, в одной плоскости);

б) разложение силы по трем заданным направлениям. Если заданные направления не лежат в одной плоскости, то задача является определенной и сводится к построению такого параллелепипеда, у которого диагональ изображает заданную силу R, а ребра параллельны заданным направлениям (см. рис. 14).