Гауссовское распределение. Правило «трёх сигма»

Нормальное распределение, также называемое гауссовым распределением или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:

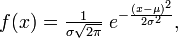где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

Нормальное распределение играет важнейшую роль во многих областях знаний, особенно в статистической физике. Физическая величина, подверженная влиянию значительного числа независимых факторов, способных вносить с равной погрешностью положительные и отрицательные отклонения, вне зависимости от природы этих случайных факторов, часто подчиняется нормальному распределению, поэтому из всех распределений в природе чаще всего встречается нормальное (отсюда и произошло одно из названий этого распределения вероятностей).

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

Свойства:

Если случайные величины Х1 и Х2 независимы и имеют нормальное распределение с математическими ожиданиями 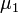и и 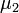дисперсиям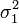и и 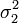соответственно, то 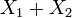также имеет нормальное распределение с математическим ожиданием 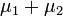и дисперсией .

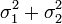Моделирование нормальных случайных величин

Простейшие, но неточные методы моделирования основываются на центральной предельной теореме. Именно, если сложить много независимых одинаково распределённых величин с конечной дисперсией, то сумма будет распределена примерно нормально. Например, если сложить 12 независимых базовых случайных величин, получится грубое приближение стандартного нормального распределения. Тем не менее, с увеличением слагаемых распределение суммы стремится к нормальному.

Использование точных методов предпочтительно, поскольку у них практически нет недостатков. В частности, преобразование Бокса — Мюллера является точным, быстрым и простым для реализации методом генерации.

Правило «трёх сигм»

В теории вероятностей квадратичное отклонение σx случайной величины x (от ее математического ожидания) определяется как квадратный корень из дисперсии Dx и называют также стандартным отклонением величины x. Для любой случайной величины x с математическим ожиданием mx и квадратичным отклонением σx вероятность отклонения x от mx, больших по абсолютной величине k·σx, k > 0, не превосходит 1/k2 (неравенство Чебышева). В случае нормального распределения указанная вероятность при k = 3 равна 0.0027. В практических задачах, приводящих к нормальному распределению, чаще всего пренебрегают возможностью отклонения от среднего, большего 3·σx.

16. Системы случайных величин. Функции распределения вероятностей системы двух случайных величин. (двумерного случайного вектора) , её свойства.

Существенный интерес в математической статистике представляет рассмотрение системы двух и более случайных величин и их статистическая взаимосвязь друг с другом.

По аналогии с рядом распределения одной дискретной величины Х для двух дискретных случайных величин X и Y строится матрица распределения – прямоугольная таблица, в которой записаны все вероятности pi j = P{ X = xi , Y = yj } , i = 1, … , n; j = 1,…, m.

События (или опыты) называются независимыми, если вероятность появления (исхода) каждого из них не зависит от того, какие события (исходы) имели место в других случаях (опытах).

Две случайные величины X и Y называются независимыми, если независимы все связанные с ними события: например, {X < а} и {Y < b} или {X = xi} и {Y = yi} и т.д.

В терминах законов распределения справедливо также следующее определение: две случайные величины X и Y называются независимыми, если закон распределения каждой из них не зависит от принятого значения другой.

Совместной функцией распределения системы двух случайных величин ( X, Y ) называется вероятность совместного выполнения неравенств X < х и Y < у :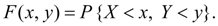

Событие 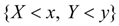означает произведение (совместное выполнение) событий {X < х} и {Y < у}.

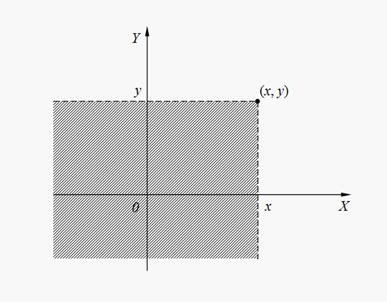
Геометрической интерпретацией совместной функции распределения F ( x, y) является вероятность попадания случайной точки ( X, Y ) на плоскости внутрь бесконечного квадранта с вершиной в точке (x, y) (заштрихованная область на рис. 8).

Основные свойства совместной функции распределения:

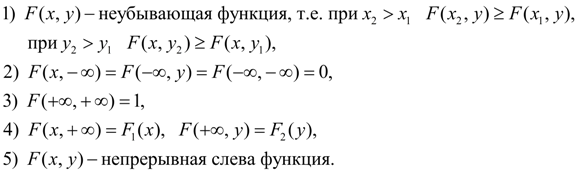
Здесь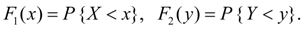

Система двух случайных величин ( X, Y ) называется непрерывной, если ее совместная функция распределения F (x, y) – непрерывная функция, дифференцируемая по каждому аргументу, у которой существует вторая смешанная частная производная .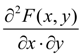

Обе случайные величины X и Y – непрерывны. Тогда функция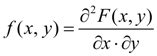

называется совместной плотностью распределения системы двух случайных величин ( X, Y ).