Вероятности суммы и произведения случайных событий (теорема сложения)

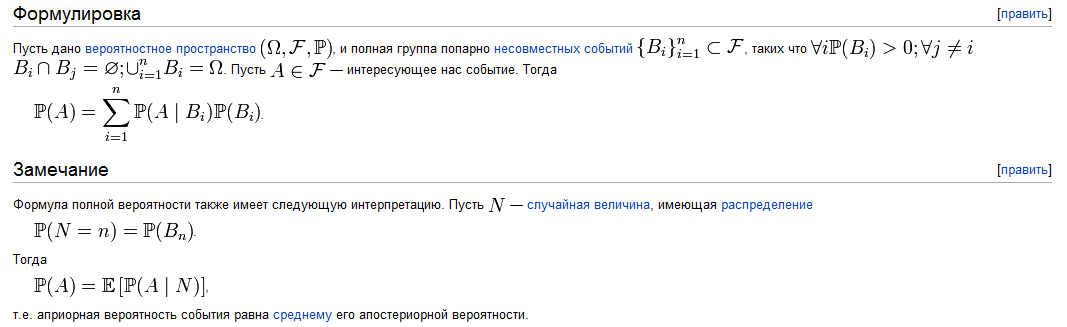
Всего исходов N, благоприятствующих событию А- К, событию В- L, совместному появлению А и В- М. Следовательно, благоприятных исходов для события А+В : K+L-M. Откуда вероятность события А+В:

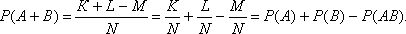
Решим задачи: Пример1. Найти вероятность суммы противоположных событий.

Решение: События А и А несовместны, следовательно Р( А +А ) = Р(А) + Р( А). Сумма двух противоположных событий есть событие достоверное, поэтому Р( А +А )= 1. Тогда Р(А) + Р( А ) =1. Отсюда следует :Р( А) = 1 - Р(А).

Пример2. В урне 3 красных, 5 синих и 2 белых шара. Наудачу вынимают один шар. Какова вероятность того, что шар окажется цветным?

Решение: Пусть событие А- вынут синий шар, событие В- красный шар. Эти события несовместны. Интересующее событие- вынут цветной шар, означает, что вынут красный или синий, т.е. событие А+В. используем теорему о сумме несовместных событий Р(А+В)=Р(А)+Р(В). вычислим вероятности событий А и В:

Р(А)=5/10=1/2; Р(В)=3/10. Тогда искомая вероятность равна Р(А+В) = 1/2+3/10= 8/10=0,8.

Условные вероятности. Теорема умножения вероятностей. Формула полной вероятности. Формула Байеса

Условной вероятностью 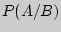события 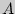при условии, что событие 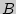произошло 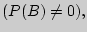назовем отношение .

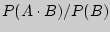Это определение эквивалентно так называемой теореме умножения, согласно которой 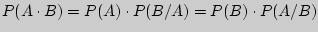, т.е. вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого при условии, что первое событие наступило.

Два события и называются независимыми, если .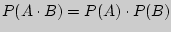

Построение классической вероятности основано на правилах сложения и умножения вероятностей, следствия которых имеют следующие интерпретации на вероятностных деревьях:

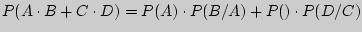где и -несовместные события

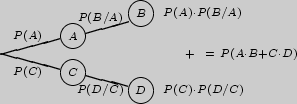
2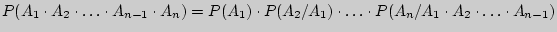

Назовем произведение 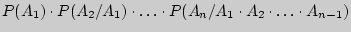весом ветви, проходящей через корень дерева и вершины, соответствующие событиям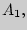

нтерпретацией теорем сложения и умножения на вероятностных деревьях служит дерево исходов, соответствующее "благоприятному" событию. Рядом с каждым ребром такого дерева запишем вероятность исхода, соответствующего конечной вершине этого ребра при условии выполнения произведения всех исходов, соответствующих вершинам пути от корня дерева до данной вершины.

Эффективность данных интерпретаций покажем на следующих примерах.

Слово "МАТЕМАТИКА" разделено на отдельные буквы, из них произвольным образом отбираются и выкладываются по порядку четыре буквы. Какова вероятность получения слова "МАМА"?

Решение. Пусть событие А= {получить слово "МАМА"}. Возьмем в дереве испытаний ветвь, соответствующую событиюА и найдем ее вес:

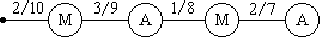
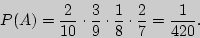
Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.