Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении. Уравнения поступательного движения.
Коэффициент трения качения
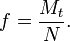 Mt — момент силы трения в [Н] · [м];
Mt — момент силы трения в [Н] · [м];
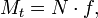 действующий против часовой стрелки (относительно мгновенного центра вращения в зоне контакта — правого конца отрезка f) и тормозящий качение тела вправо; N — прижимающая сила; f — коэффициент трения качения, равный длине плеча силы N.
действующий против часовой стрелки (относительно мгновенного центра вращения в зоне контакта — правого конца отрезка f) и тормозящий качение тела вправо; N — прижимающая сила; f — коэффициент трения качения, равный длине плеча силы N.
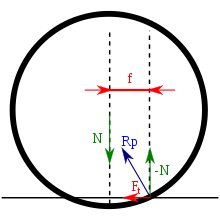 Коэффициент трения f;
Коэффициент трения f; 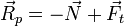 — асимметричная реакция опорной поверхности, векторная сумма вертикальной
— асимметричная реакция опорной поверхности, векторная сумма вертикальной 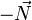 и горизонтальной
и горизонтальной 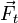 компонент;
компонент; 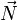 — прижимающая сила;
— прижимающая сила; 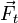 — сила трения качения.
— сила трения качения.
Коэффициент трения качения имеет следующие физические интерпретации:
· Если тело находится в покое и внешняя сила отсутствует, то реакция опоры лежит на той же линии, что и прижимающая сила. Когда тело катится, то из условия равновесия следует, что нормальная составляющая реакции опоры параллельна и противонаправлена прижимающей силе, но не лежит с ней на одной линии. Коэффициент трения качения равен расстоянию между прямыми, вдоль которых действуют прижимающая сила и нормальная составляющая реакции опоры
· Движение катящегося тела без проскальзывания можно рассматривать как поворот вокруг мгновенной оси вращения (на рис. 4 — точка приложения вектора 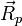 ), которая для абсолютно твёрдых тел совпадает с основанием перпендикуляра, опущенного из центра круга на опору. Для случая реальных (деформирующихся под нагрузкой) материалов мгновенный центр вращения смещён в направлении качения тела, а величина смещения равна значению коэффициента трения качения.
), которая для абсолютно твёрдых тел совпадает с основанием перпендикуляра, опущенного из центра круга на опору. Для случая реальных (деформирующихся под нагрузкой) материалов мгновенный центр вращения смещён в направлении качения тела, а величина смещения равна значению коэффициента трения качения.
 16) Равнодействующая
16) Равнодействующая 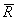 двух параллельных сил, направленных в одну сторону, параллельна этим силам и направлена в ту же сторону; модуль равнодействующей равен сумме модулей данных сил, а линия действия равнодействующей делит расстояние между точками приложения данных сил внутренним образом на части, обратно пропорциональные модулям этих сил, т.е.
двух параллельных сил, направленных в одну сторону, параллельна этим силам и направлена в ту же сторону; модуль равнодействующей равен сумме модулей данных сил, а линия действия равнодействующей делит расстояние между точками приложения данных сил внутренним образом на части, обратно пропорциональные модулям этих сил, т.е.
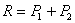 ;
; 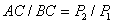 .
.
Используя известное свойство пропорции, можно получить
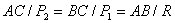 .
.
Пусть теперь имеем две параллельные силы 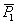 и
и 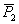 , приложенные в точках
, приложенные в точках 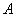 и
и 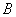 и направленные в противоположные стороны; такие силы называются антипараллельными.
и направленные в противоположные стороны; такие силы называются антипараллельными.
Предположим, что  >
>  . Равнодействующая
. Равнодействующая 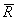 двух антипараллельных сил параллельна этим силам и направлена в сторону большей силы; модуль равнодействующей равен разности модулей данных сил, а линия ее действия делит расстояние между точками приложения данных сил внешним образом на части, обратно пропорциональные модулям этих сил, т.е.
двух антипараллельных сил параллельна этим силам и направлена в сторону большей силы; модуль равнодействующей равен разности модулей данных сил, а линия ее действия делит расстояние между точками приложения данных сил внешним образом на части, обратно пропорциональные модулям этих сил, т.е.
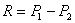 ;
; 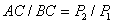 и
и 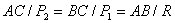 .
.
Как видно, в этом случае линия действия равнодействующей 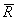 проходит через точку, лежащую вне отрезка
проходит через точку, лежащую вне отрезка 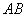 , и притом ближе к большей силе.
, и притом ближе к большей силе.
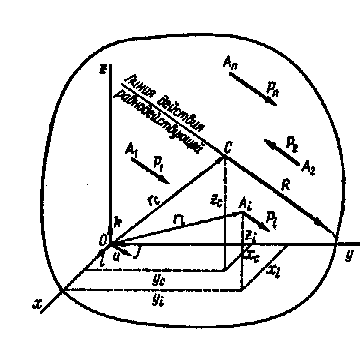
Рассмотрим систему параллельных сил 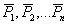 , приложенных в точках
, приложенных в точках 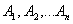 , приводящуюся к равнодействующей
, приводящуюся к равнодействующей 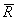 , приложенной в точке
, приложенной в точке 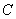
Положение центра параллельных сил 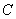 определится его радиусом-вектором
определится его радиусом-вектором 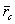 относительно начала координат
относительно начала координат 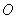 или тремя координатами
или тремя координатами 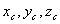 . Положение точки приложения каждой силы
. Положение точки приложения каждой силы 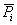 определяется радиусом-вектором
определяется радиусом-вектором 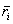 или координатами
или координатами 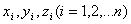 .
.
Опуская выкладки, приведем формулу, определяющую радиус-вектор центра параллельных сил
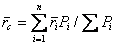 . (10)
. (10)
Спроектировав равенство (5) на оси координат, получим формулы для определения координат центра параллельных сил
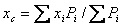 ;
;  ;
; 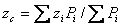 . (11)
. (11)
В формулах (11) координаты 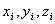 и значения сил
и значения сил 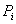 являются алгебраическими величинами. Заметим, что выбор направления, вдоль которого параллельные силы считаются положительными, произволен и на результатах вычисления координат по формулам (11) не отражается.
являются алгебраическими величинами. Заметим, что выбор направления, вдоль которого параллельные силы считаются положительными, произволен и на результатах вычисления координат по формулам (11) не отражается.
17) Центр тяжести
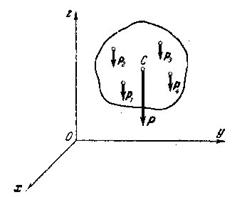
Представим себе какое-нибудь твердое тело, находящееся близ поверхности Земли (рис.1). Силы притяжения 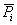 отдельных частиц тела к Земле направлены приблизительно к центру Земли. Так как размеры рассматриваемых тел малы по сравнению с радиусом Земли, то эти силы можно считать параллельными. Центр
отдельных частиц тела к Земле направлены приблизительно к центру Земли. Так как размеры рассматриваемых тел малы по сравнению с радиусом Земли, то эти силы можно считать параллельными. Центр 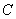 этой системы параллельных сил называется центром тяжести данного тела, а равнодействующая этих сил
этой системы параллельных сил называется центром тяжести данного тела, а равнодействующая этих сил 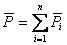 , проходящая через точку
, проходящая через точку  , представляет собой вес этого тела.
, представляет собой вес этого тела.
Так как центр тяжести тела есть центр параллельных сил, то для вычисления координат центра тяжести тела можно воспользоваться формулами, приведенными в предыдущем модуле
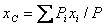 ,
, 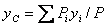 ,
, 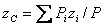 (16)
(16)
где 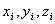 - координаты любой частицы твердого тела.
- координаты любой частицы твердого тела.
Заметим, что в (16) алгебраическими величинами являются только координаты точек, а значения 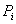 всегда положительны, так как все силы направлены в одну сторону.
всегда положительны, так как все силы направлены в одну сторону.
Обозначим объемы элементарных частиц через 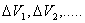 , а вес единицы объема тела через
, а вес единицы объема тела через 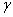 . Если тело однородно, то получим
. Если тело однородно, то получим
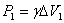 ,
, 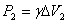 ,……
,……
Подставив эти значения сил 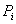 в формулы (2), будем иметь
в формулы (2), будем иметь
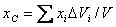 ,
, 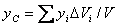 ,
, 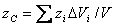 , (17)
, (17)
где 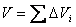 - объем всего тела.
- объем всего тела.
Для получения точных формул координат центра тяжести однородного тела, нужно в формулах (17) перейти к пределу, полагая, что число элементарных частиц неограниченно возрастает, а объем 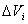 каждой частицы стремится к нулю
каждой частицы стремится к нулю
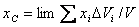 ,
, 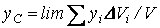 ,
, 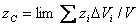 . (18)
. (18)
Если имеем однородное тело, имеющее форму тонкой пластинки, то его можно рассматривать как материальную плоскую фигуру, положение центра тяжести которой определяется двумя координатами 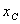 и
и 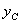 (рис.2).
(рис.2).
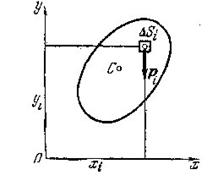
В этом случае вместо элементов объема 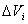 нужно брать элементы площади
нужно брать элементы площади 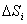 , а в знаменателе вместо
, а в знаменателе вместо  - площадь
- площадь 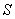 данной фигуры. Следовательно, для координат центра тяжести плоской фигуры будем иметь
данной фигуры. Следовательно, для координат центра тяжести плоской фигуры будем иметь
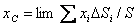 ,
, 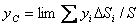 . (19)
. (19)
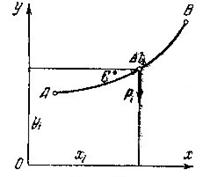
Аналогично, для координат центра тяжести однородной плоской материальной линии 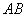 (например, тонкой проволоки, согнутой в виде плоской кривой), получим
(например, тонкой проволоки, согнутой в виде плоской кривой), получим
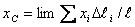 ,
, 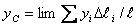 , (20)
, (20)
где 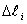 - длина элементарной дуги данной линии, а
- длина элементарной дуги данной линии, а 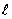 - вся длина этой линии (рис.3).
- вся длина этой линии (рис.3).
Следует отметить, что центр тяжести 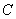 кривой линии вообще не лежит на этой линии. Вычисление пределов сумм, входящих в полученные формулы (18), (19) и (20), производится в общем случае методами интегрального исчисления; эти пределы выражаются определенными интегралами, распространенными соответственно на весь объем тела или на всю площадь фигуры или же взятыми вдоль данной линии.
кривой линии вообще не лежит на этой линии. Вычисление пределов сумм, входящих в полученные формулы (18), (19) и (20), производится в общем случае методами интегрального исчисления; эти пределы выражаются определенными интегралами, распространенными соответственно на весь объем тела или на всю площадь фигуры или же взятыми вдоль данной линии.
18) Способы определения положения центров тяжести тел. Способ группировки. Центр тяжести. Приведем вспомогательную теорему для определения положения центра тяжести: если однородное тело имеет плоскость, или ось, или центр симметрии, то центр тяжести такого тела лежит соответственно в этой плоскости, на этой оси или в этом центре симметрии.
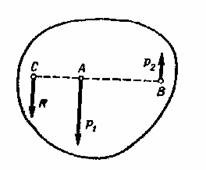
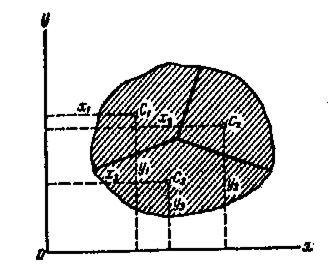 Теперь перейдем к определению положения центра тяжести плоской фигуры сложной формы. Пусть требуется определить положение центра тяжести плоской фигуры, состоящей из трех частей, положение центров тяжести которых известно (рис1).
Теперь перейдем к определению положения центра тяжести плоской фигуры сложной формы. Пусть требуется определить положение центра тяжести плоской фигуры, состоящей из трех частей, положение центров тяжести которых известно (рис1).
Положим, что площади частей фигуры соответственно равны 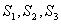 , а координаты их центров тяжести
, а координаты их центров тяжести 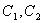 и
и 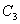 будут
будут 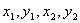 и
и 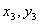 . Тогда координаты ее центра тяжести
. Тогда координаты ее центра тяжести 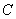 определятся формулами
определятся формулами
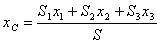 ;
; 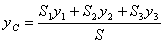 . (21)
. (21)
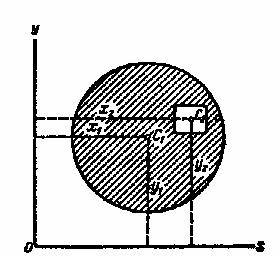 Этими формулами удобно пользоваться и при определении положения центра тяжести плоской фигуры, из которой вырезана некоторая часть (рис.2).
Этими формулами удобно пользоваться и при определении положения центра тяжести плоской фигуры, из которой вырезана некоторая часть (рис.2).
В этом случае координаты центра тяжести выражаются формулами
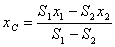 ,
, 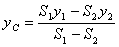 , (22)
, (22)
где 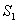 и
и 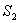 - площади соответственно всей фигуры и вырезанной из нее части, а
- площади соответственно всей фигуры и вырезанной из нее части, а 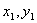 и
и 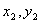 - координаты их центров тяжести.
- координаты их центров тяжести.
Этот способ определения центра тяжести плоской фигуры называется способом отрицательных площадей.
 В заключении приведем формулы для определения положения центров тяжести некоторых фигур.
В заключении приведем формулы для определения положения центров тяжести некоторых фигур.
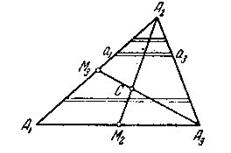
а) Центр тяжести площади треугольника
Центр тяжести 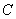 площади треугольника совпадает с точкой пересечения его медиан
площади треугольника совпадает с точкой пересечения его медиан 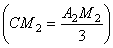 .
.
Если обозначить координаты вершин данного треугольника через ( 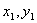 ), (
), ( 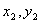 ), (
), ( 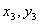 ), то для координат
), то для координат 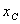 и
и 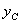 его центра тяжести получим
его центра тяжести получим
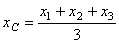 ,
, 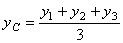 . (23)
. (23)
б) Центр тяжести дуги окружности (дуга  )
)
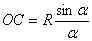 (24)
(24)
где 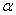 - половина центрального угла дуги
- половина центрального угла дуги 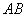 , измеряемого в радианах.
, измеряемого в радианах.
в) Центр тяжести площади кругового сектора ( 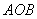 )
)
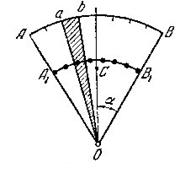
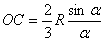 (25)
(25)
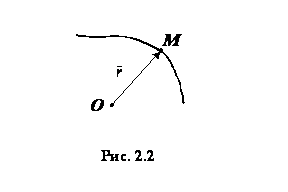 19) Движение точки может быть задано тремя способами: естественным, векторным и координатным.
19) Движение точки может быть задано тремя способами: естественным, векторным и координатным.
При векторном способе задания движения точки положение точки 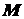 определяется величиной и направлением радиуса-вектора
определяется величиной и направлением радиуса-вектора 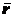 , проведенного из неподвижного центра
, проведенного из неподвижного центра 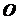 в данную точку (рис. 2.2). При движении точки ее радиус-вектор
в данную точку (рис. 2.2). При движении точки ее радиус-вектор 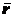 изменяется по величине и направлению. Поэтому, чтобы определить положение точки в любой момент времени, достаточно задать ее радиус-вектор
изменяется по величине и направлению. Поэтому, чтобы определить положение точки в любой момент времени, достаточно задать ее радиус-вектор 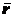 как функцию времени:
как функцию времени: 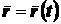 . (2.2)
. (2.2)
Это равенство называется векторным уравнением движения точки. Очевидно, что траектория точки представляет собой геометрическое место точек концов радиуса-вектора 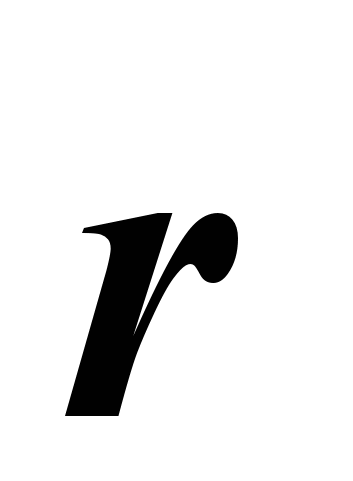 .
.
Скорость и ускорение точки при векторном способе задания движения
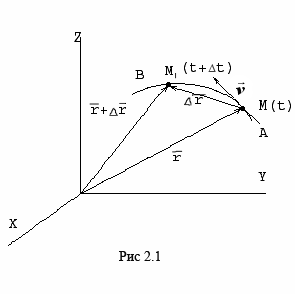 Скорость точки – это величина, характеризующая как быстро и в каком направлении меняется положение точки в пространстве. Поскольку она определяет направление перемещения точки, скорость является величиной векторной.
Скорость точки – это величина, характеризующая как быстро и в каком направлении меняется положение точки в пространстве. Поскольку она определяет направление перемещения точки, скорость является величиной векторной. 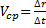 (2.1)
(2.1)
Этот вектор направлен так же, как и 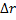 . Предельное значение
. Предельное значение 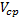 , при стремящемся к нулю
, при стремящемся к нулю 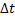 , определит мгновенное значение скорости в данный момент времени
, определит мгновенное значение скорости в данный момент времени
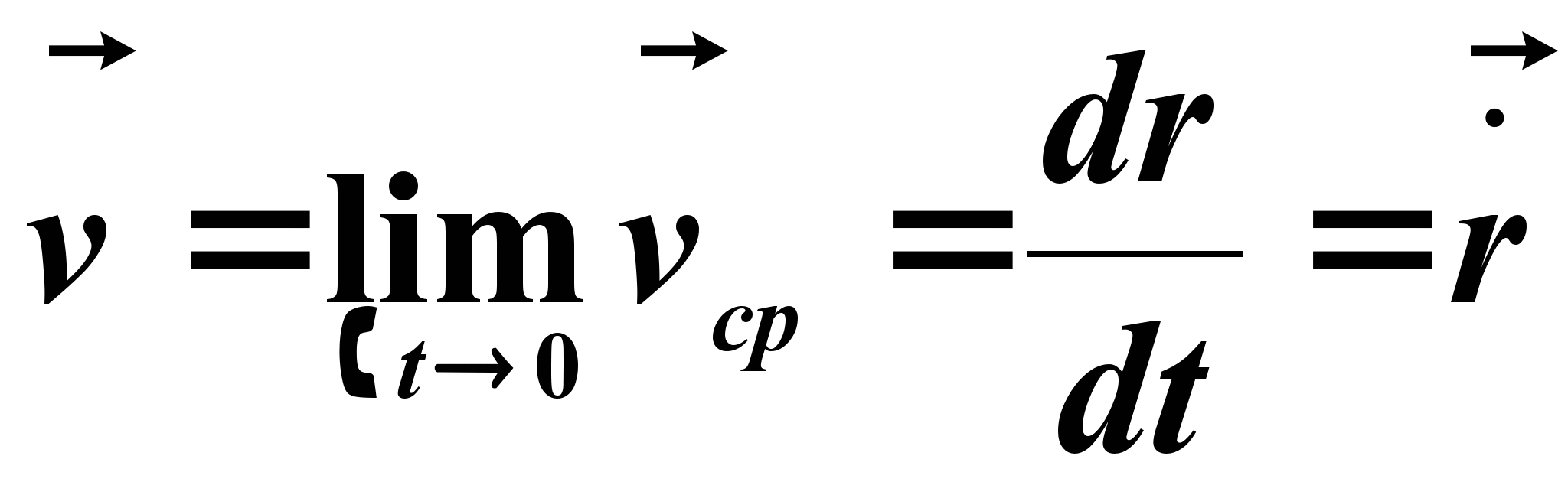 (2.2)
(2.2)
При стремлении 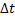 к нулю хорда ММ1, а значит и вектор
к нулю хорда ММ1, а значит и вектор 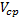 поворачивается вокруг точки М, приближаясь к касательной к траектории в точке М и в пределе, совпадая с ней. Поэтому вектор V направлен по касательной к траектории точки в сторону движения.
поворачивается вокруг точки М, приближаясь к касательной к траектории в точке М и в пределе, совпадая с ней. Поэтому вектор V направлен по касательной к траектории точки в сторону движения.
В общем случае криволинейного движения вектор скорости изменяется по величине и направлению в функции времени. Следовательно, за время 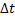 вектор V1 можно представить в виде V1=V+
вектор V1 можно представить в виде V1=V+ 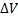 .Ускорение точки в криволинейном движении характеризует быстроту изменения вектора
.Ускорение точки в криволинейном движении характеризует быстроту изменения вектора 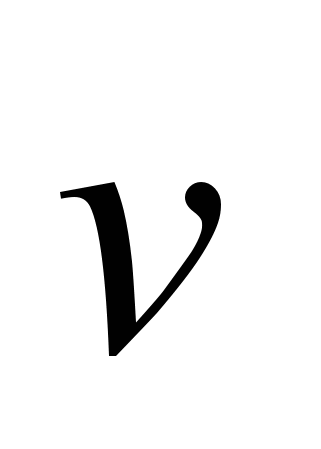 по величине и направлению. Тогда средняя величина ускорения определится
по величине и направлению. Тогда средняя величина ускорения определится  , а мгновенное значение
, а мгновенное значение
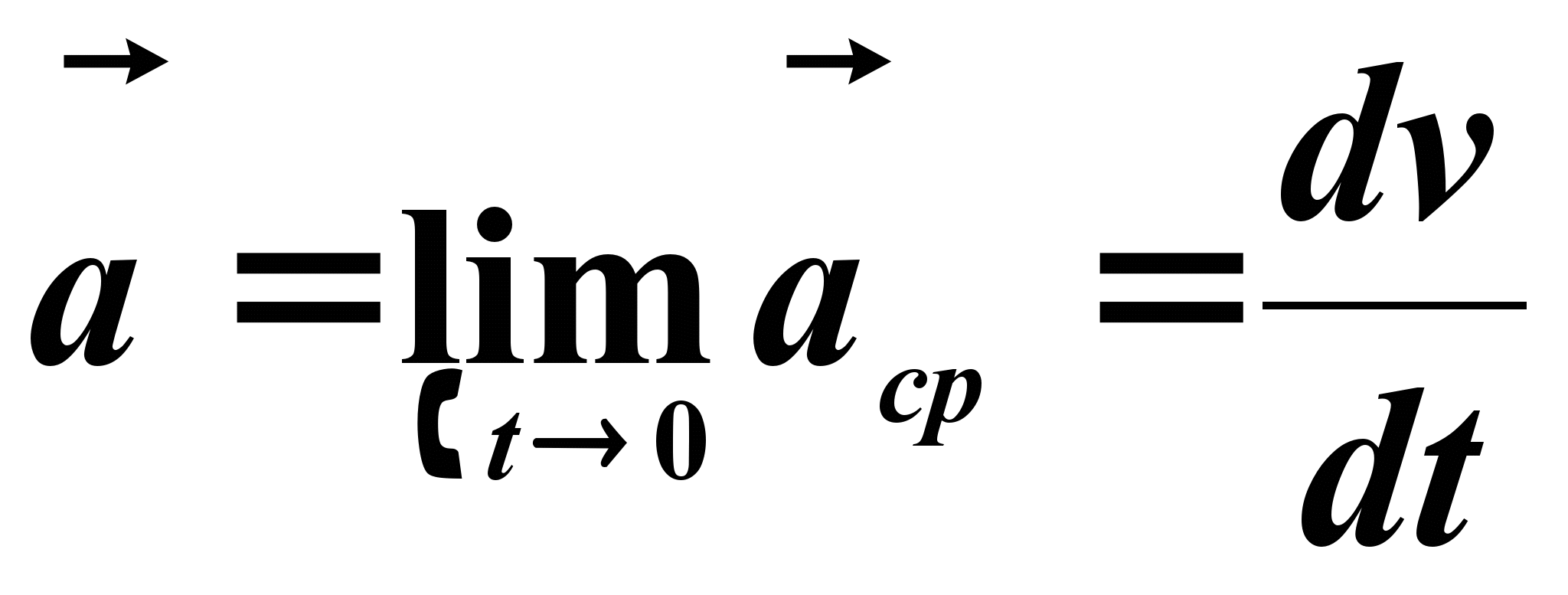 ,или
,или 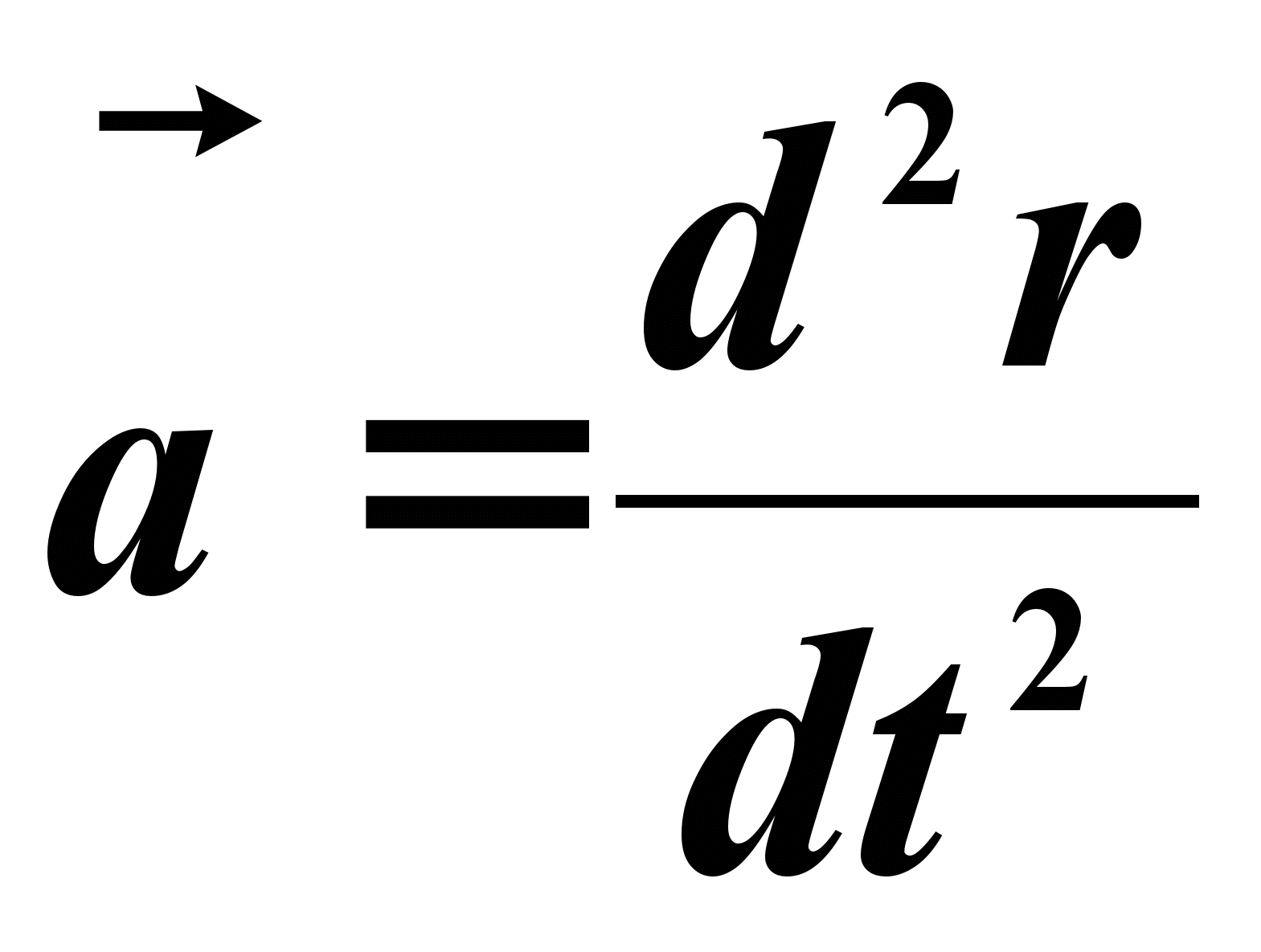 (2.3)
(2.3)
20) При координатном способе задания движения положение точки по отношению к выбранной 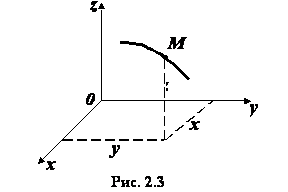 системе отсчета определяется при помощи прямоугольной системы декартовых координат (рис. 2.3). При движении точки ее координаты изменяются с течением времени. Поэтому, чтобы определить положение точки в любой момент времени, достаточно задать координаты
системе отсчета определяется при помощи прямоугольной системы декартовых координат (рис. 2.3). При движении точки ее координаты изменяются с течением времени. Поэтому, чтобы определить положение точки в любой момент времени, достаточно задать координаты  ,
, 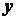 ,
, 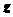 как функции времени:
как функции времени:
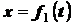 ;
; 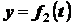 ;
; 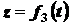 . (2.3)
. (2.3)
Эти равенства называются уравнениями движения точки в прямоугольных декартовых координатах. Движение точки в плоскости определяется двумя уравнениями системы (2.3), прямолинейное движение — одним.
Между тремя описанными способами задания движения существует взаимная связь, что позволяет от одного способа задания движения перейти к другому. В этом легко убедиться, например, при рассмотрении перехода от координатного способа задания движения к векторному.
Положим, что движение точки задано в виде уравнений (2.3). Имея в виду, что
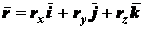 и
и  ;
; 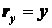 ;
;  , можно записать
, можно записать 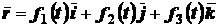 .
.
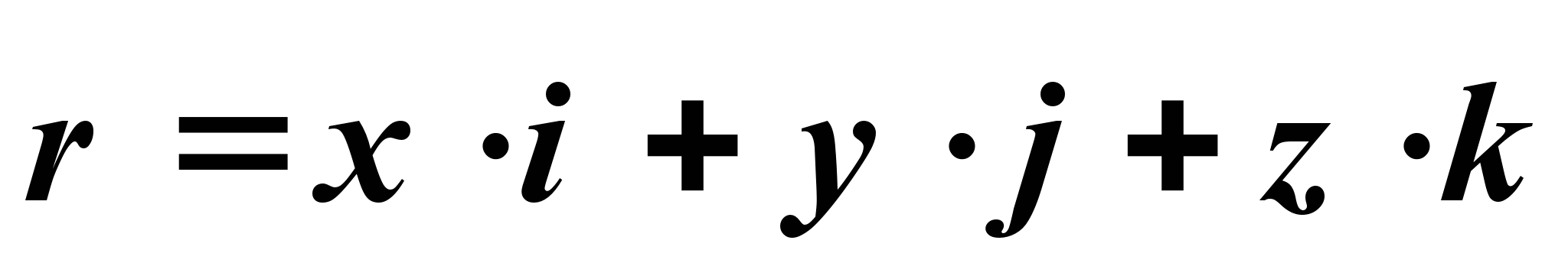 Скорость и ускорение точки при координатном способе задания движения
Скорость и ускорение точки при координатном способе задания движения
Положение точки можно определить и через радиус-вектор 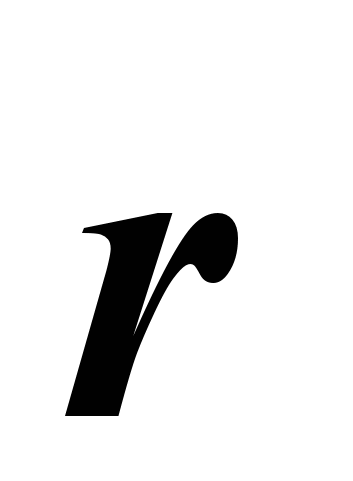 . Он может быть представлен с помощью единичных векторов и координат в виде
. Он может быть представлен с помощью единичных векторов и координат в виде
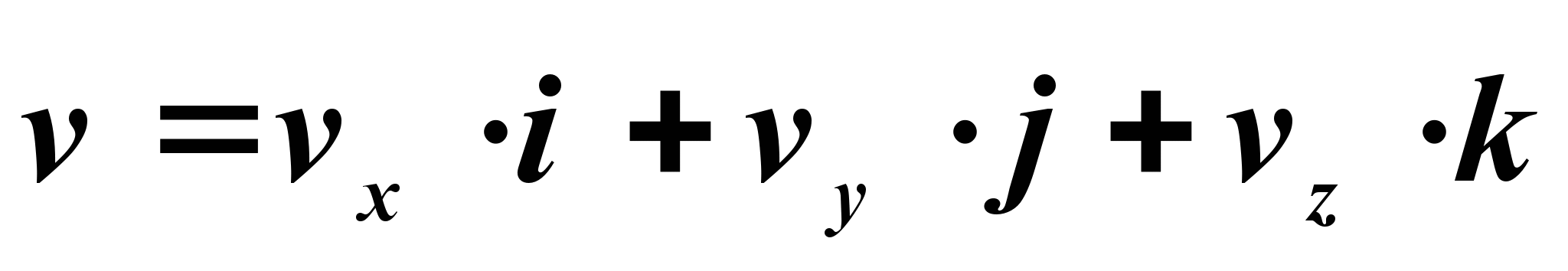 Производная по времени от будет
Производная по времени от будет
Следовательно, 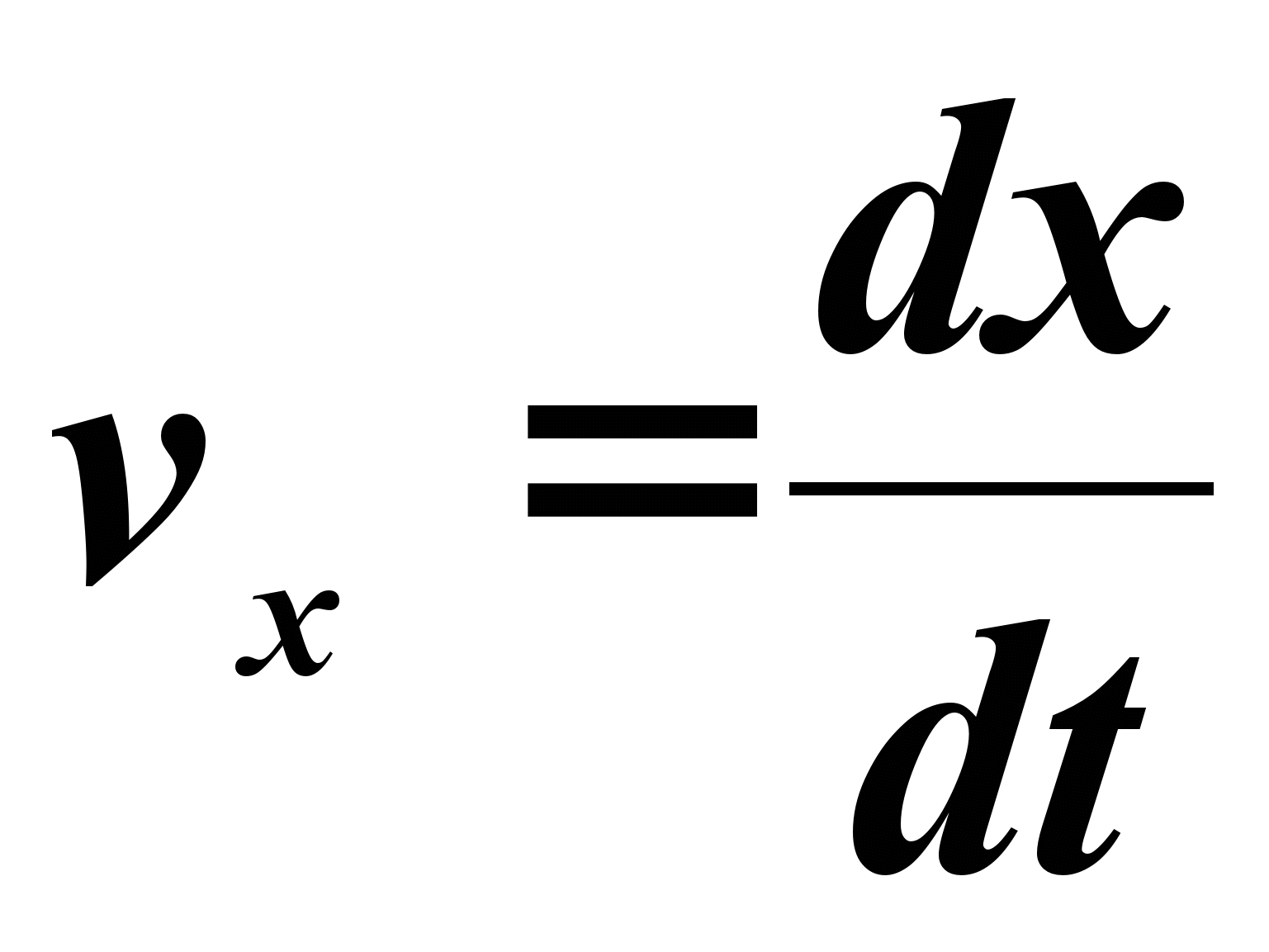
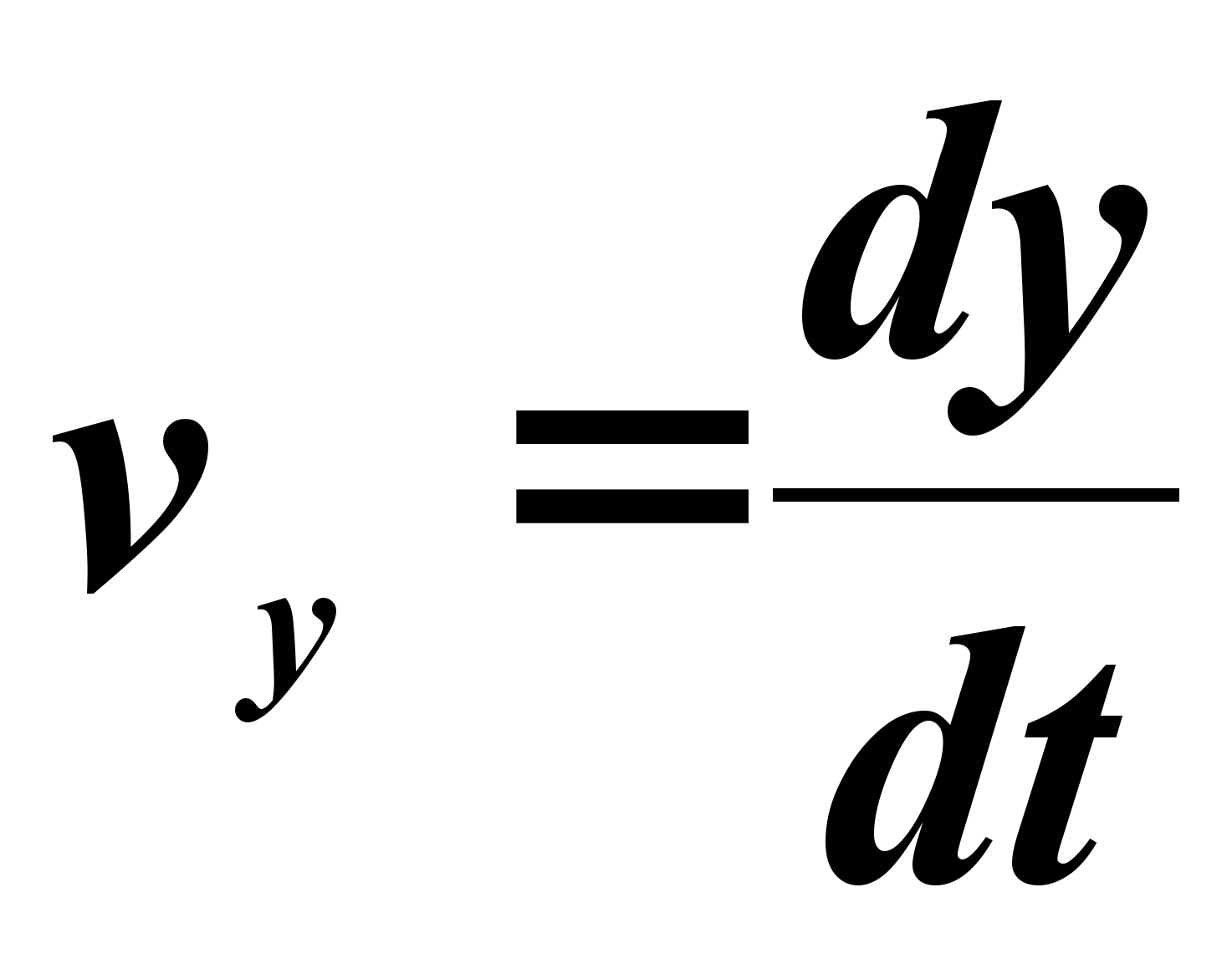
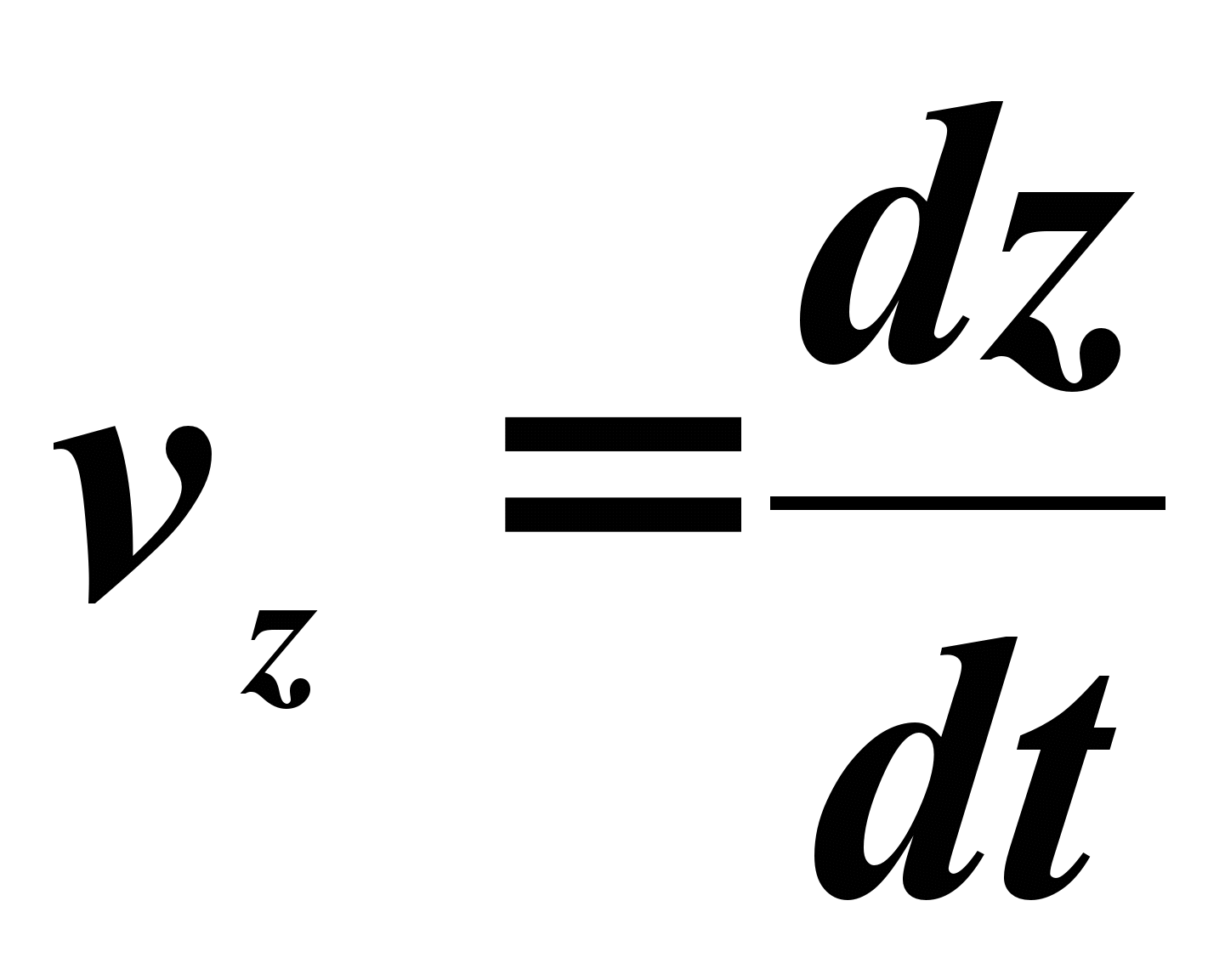
Модуль скорости определяется формулой 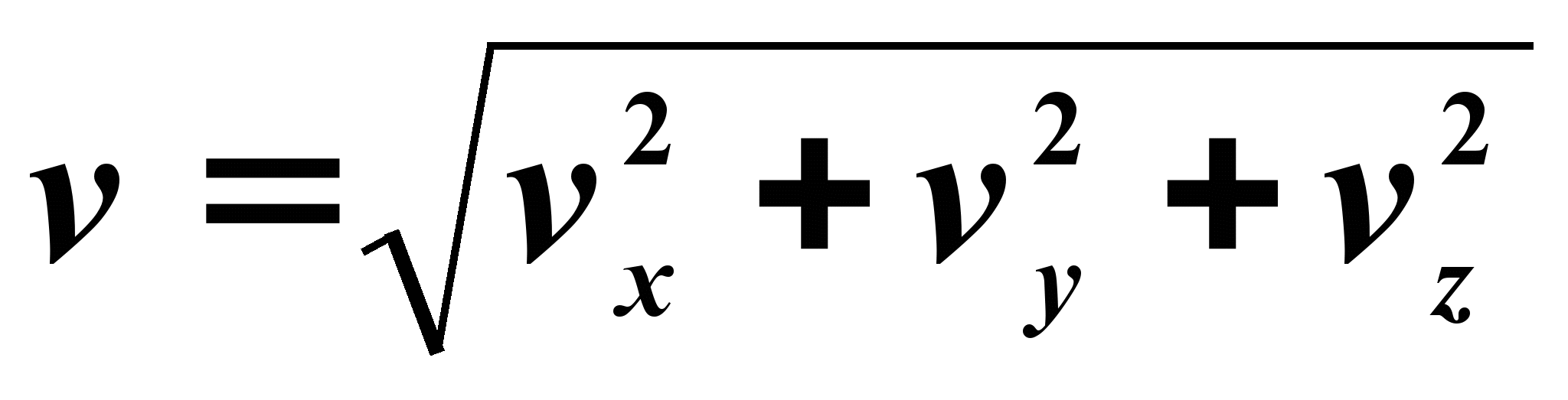
Направление вектора скорости устанавливается согласно направляющих косинусов
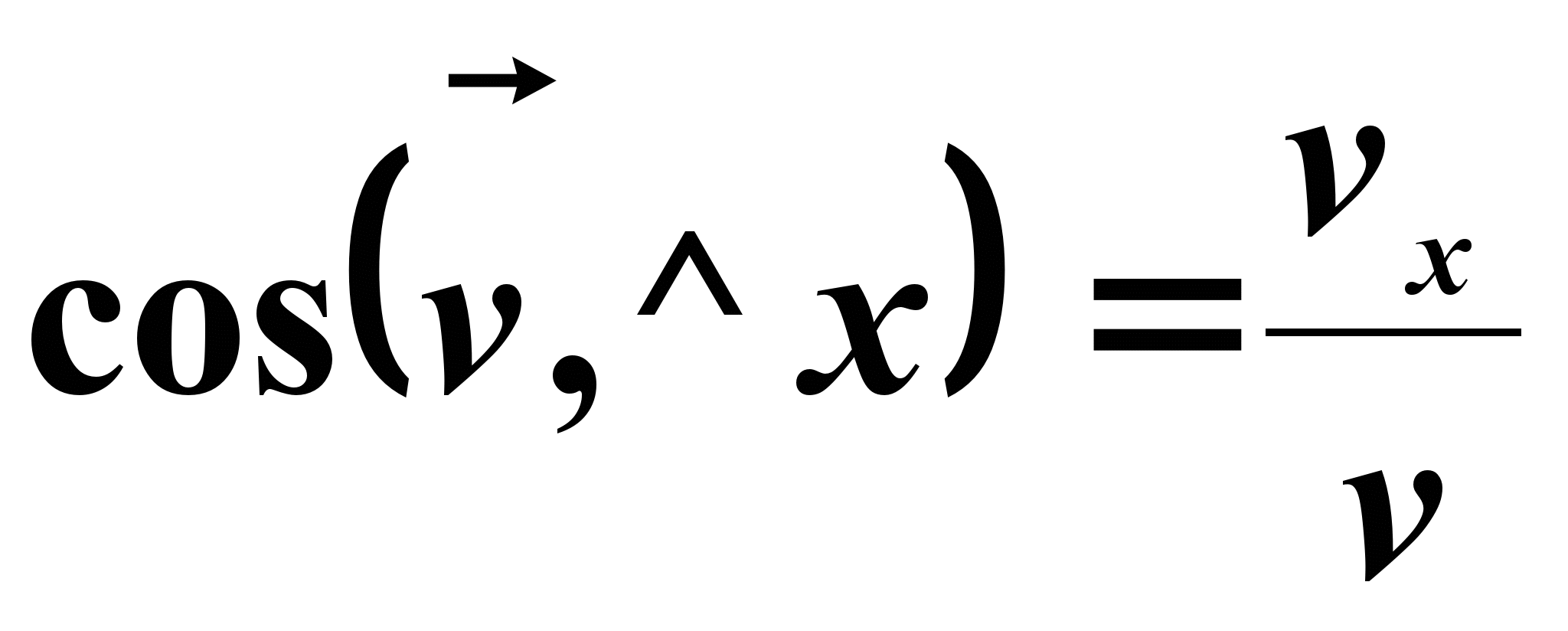
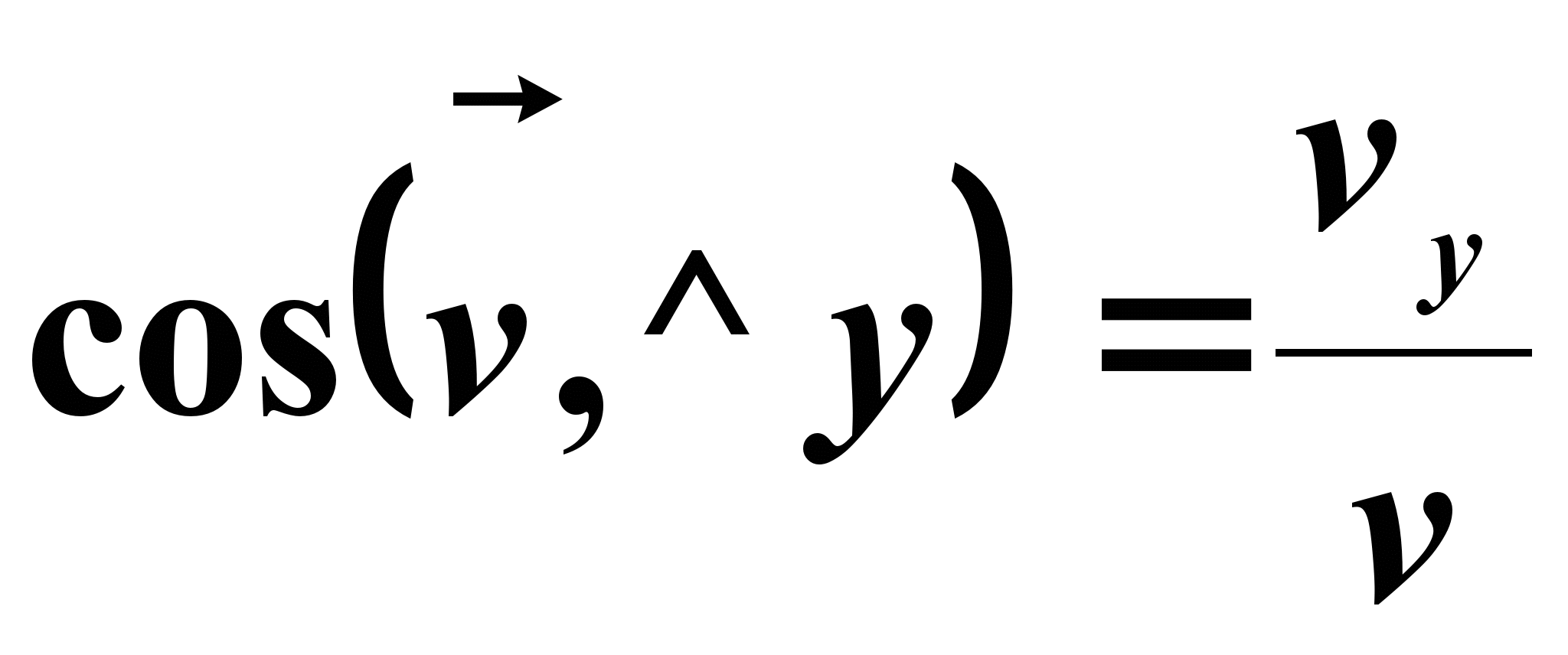
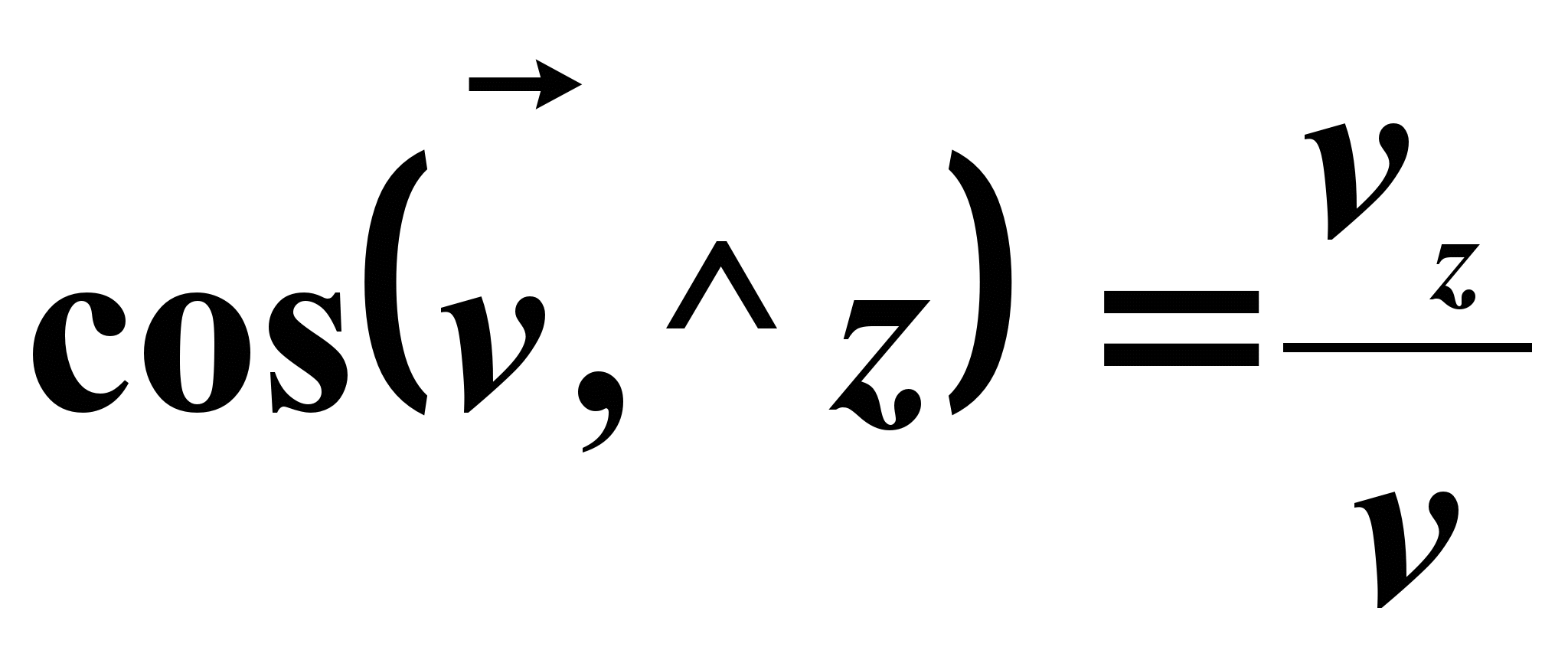
Вектор скорости направлен по касательной к траектории движения точки. По
аналогии, ускорение 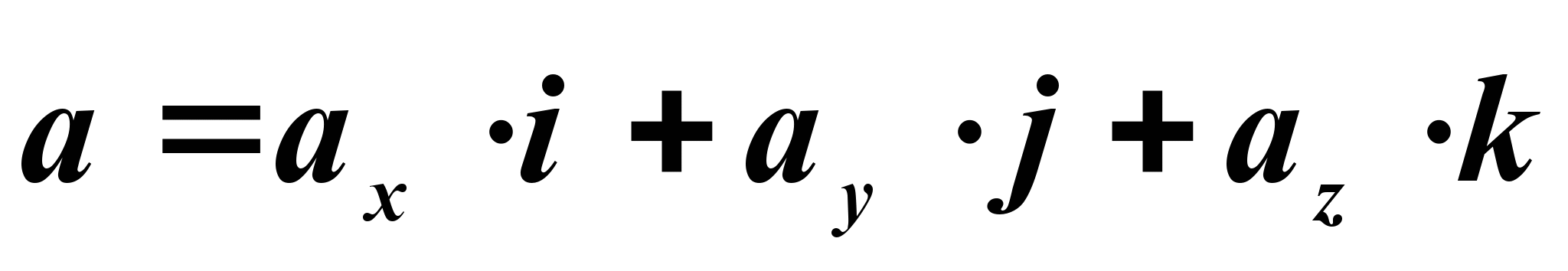
Установлено, что ускорение точки есть производная от скорости по времени или вторая производная от радиуса-вектора  по времени. Поэтому
по времени. Поэтому 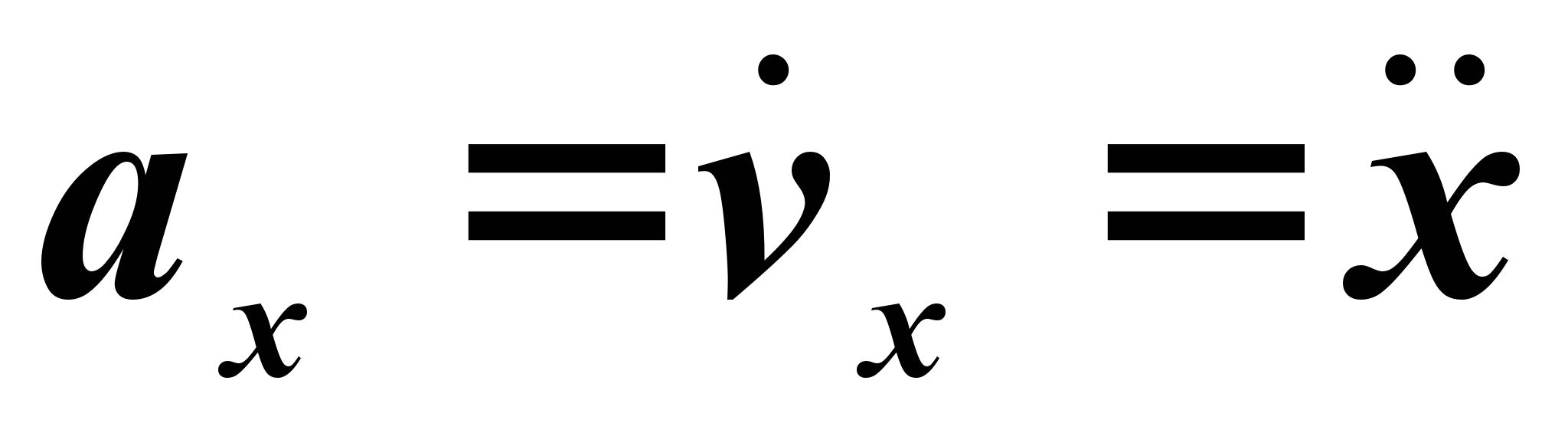
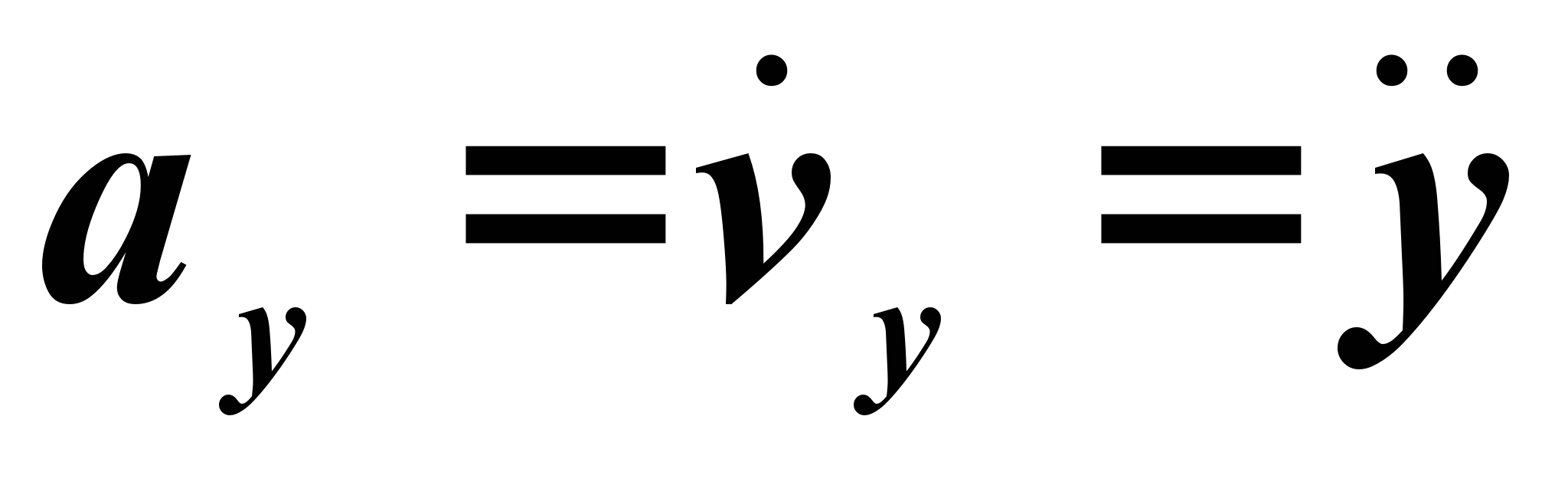
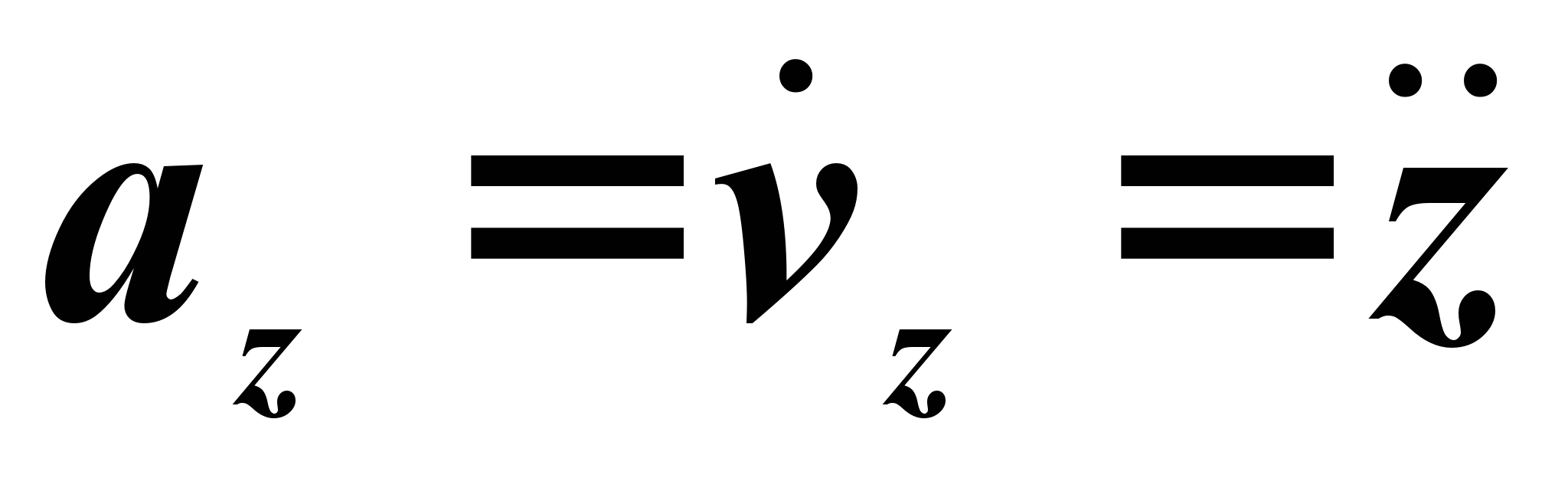
Модуль ускорения вычисляется по формуле 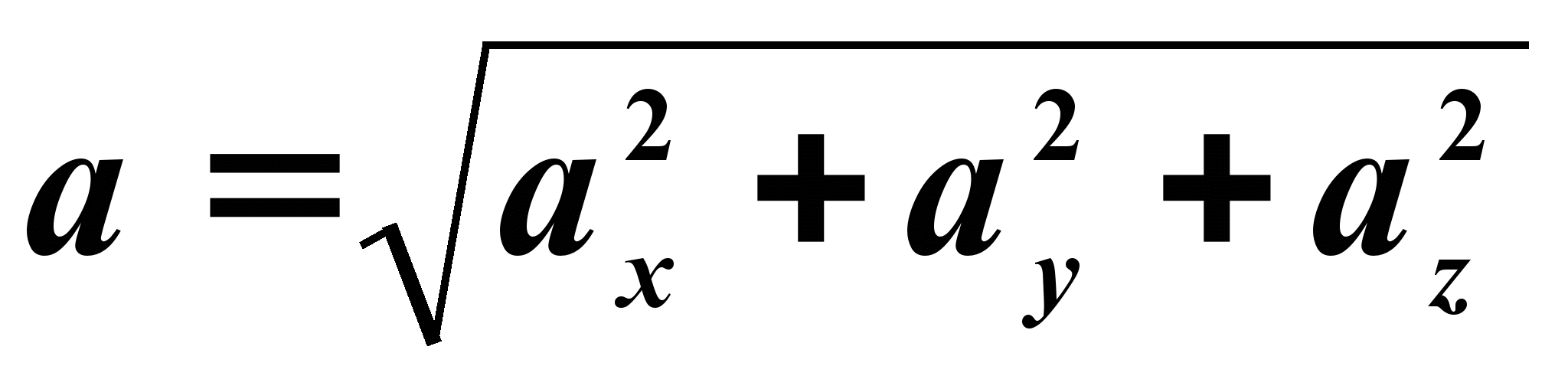
Направление вектора ускорения определяется направляющими косинусами 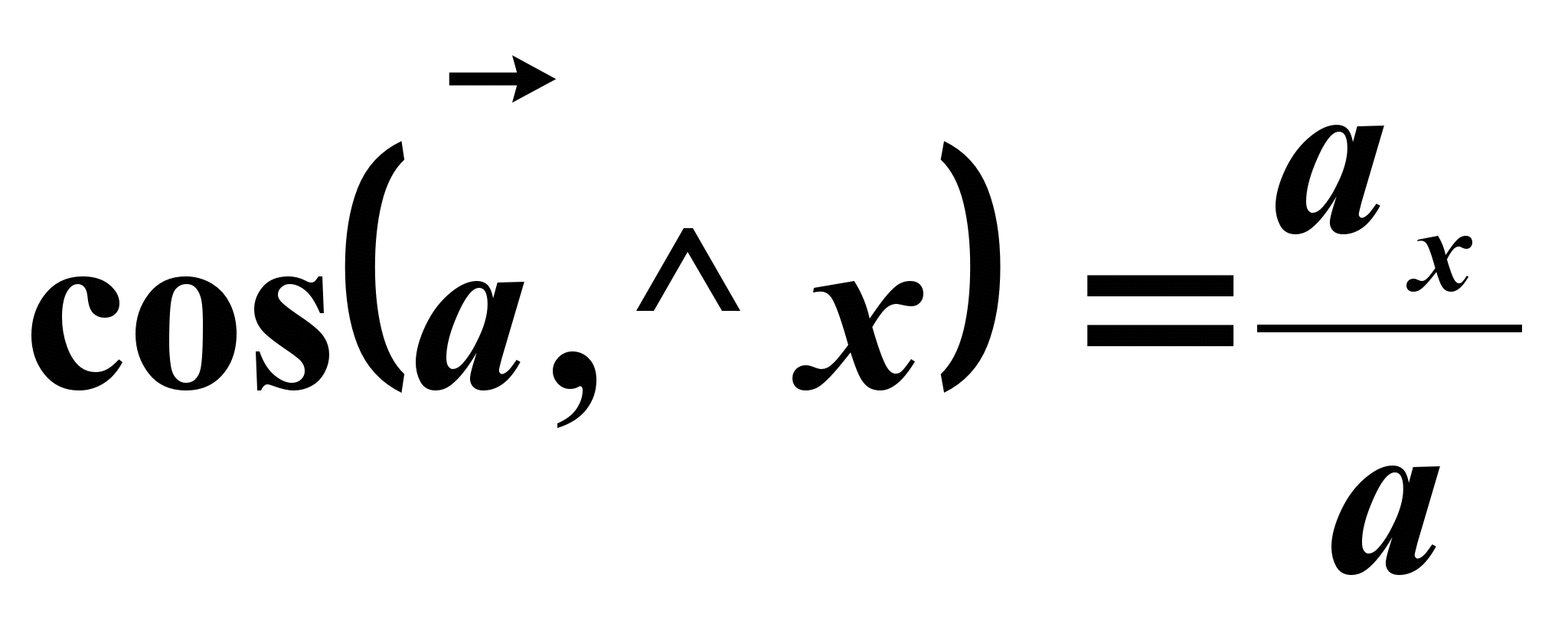
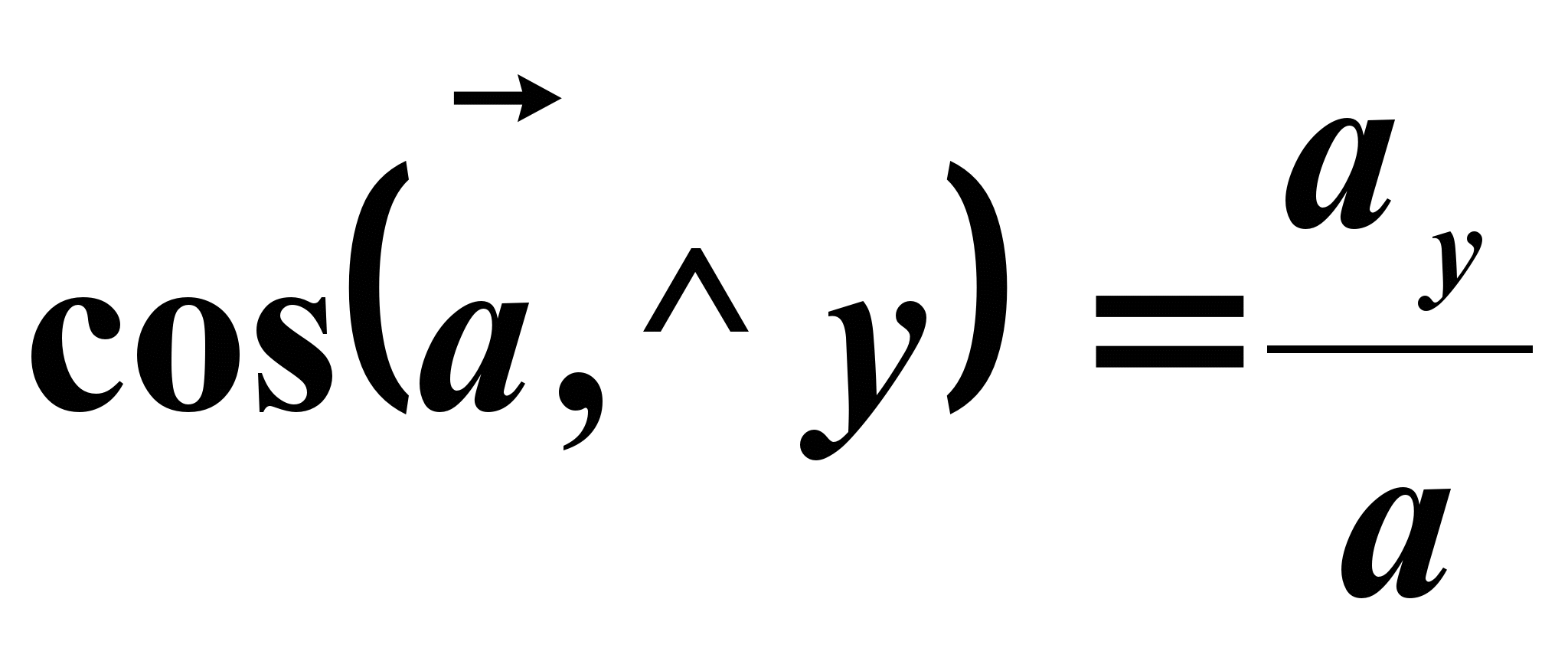
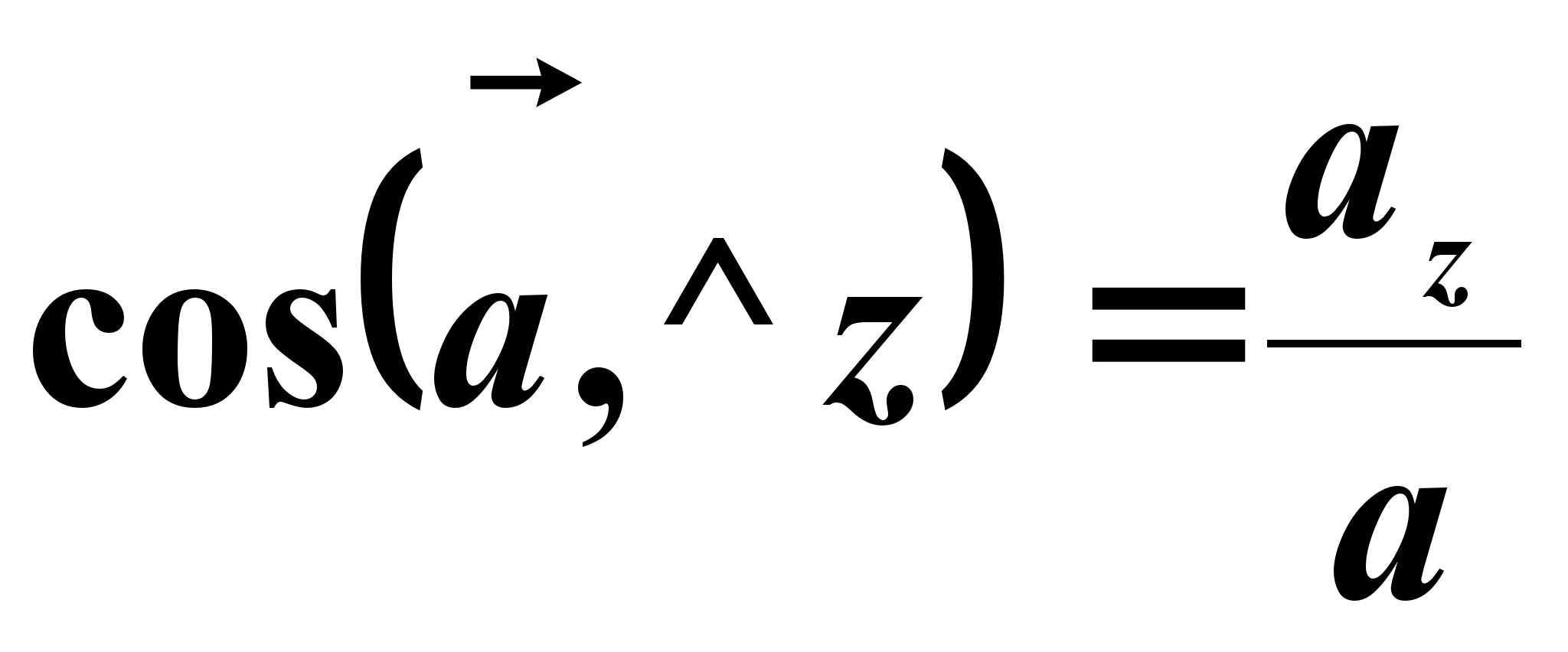
21) Естественный способ задания движения точки. Определение скорости и ускорения точки. Касательное и нормальное ускорение точки.
При естественном способе задания движения дается траектория, т. е. линия, по которой движется точка (рис.2.1)
 На этой траектории выбирается некоторая точка
На этой траектории выбирается некоторая точка  , принимаемая за начало отсчета. Выбираются положительное и отрицательное направления отсчета дуговой координаты
, принимаемая за начало отсчета. Выбираются положительное и отрицательное направления отсчета дуговой координаты 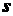 , определяющей положение точки на траектории. При движении точки расстояние
, определяющей положение точки на траектории. При движении точки расстояние 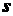 будет изменяться. Поэтому, чтобы определить положение точки в любой момент времени, достаточно задать дуговую координату
будет изменяться. Поэтому, чтобы определить положение точки в любой момент времени, достаточно задать дуговую координату 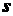 как функцию времени:
как функцию времени:
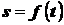 . (2.1)
. (2.1)
Это равенство называется уравнением движения точки по данной траектории.
Скорость точки V, направленная по касательной к траетории, определяется одной проекции V1, равной первой производной по времени от криволинейной координаты s: 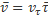 ,
, 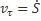
Вектор ускорения 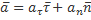 имеет проекцию
имеет проекцию 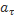 на касательную, равную первой производной по времени от проекции скорости
на касательную, равную первой производной по времени от проекции скорости 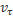 или второй производной от координаты s, и проекцию на нормаль
или второй производной от координаты s, и проекцию на нормаль 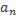 , равную отношению квадрата скорости к радиусу кривизны траектории в данной точке:
, равную отношению квадрата скорости к радиусу кривизны траектории в данной точке:
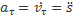
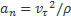
Величины 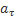 и
и 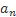 называют касательным и нормальным ускорениями точки. Касательное ускорение характеризует изменение скорости по величине, а нормальное – по направлению. τana
называют касательным и нормальным ускорениями точки. Касательное ускорение характеризует изменение скорости по величине, а нормальное – по направлению. τana
Модули скорости и ускорения точки определяются по формулам
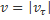
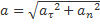
Для определения касательного ускорения точки при ее движении, заданном координатным способом с помощью функций, вводится орт касательной 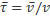 , сонаправленный с вектором скорости. Проецируя вектор ускорения
, сонаправленный с вектором скорости. Проецируя вектор ускорения 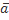 на этот орт, получаем формулу
на этот орт, получаем формулу
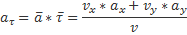
Нормальное ускорение точки
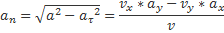
Коэффициент трения качения
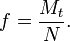 Mt — момент силы трения в [Н] · [м];
Mt — момент силы трения в [Н] · [м];
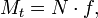 действующий против часовой стрелки (относительно мгновенного центра вращения в зоне контакта — правого конца отрезка f) и тормозящий качение тела вправо; N — прижимающая сила; f — коэффициент трения качения, равный длине плеча силы N.
действующий против часовой стрелки (относительно мгновенного центра вращения в зоне контакта — правого конца отрезка f) и тормозящий качение тела вправо; N — прижимающая сила; f — коэффициент трения качения, равный длине плеча силы N.
 Коэффициент трения f;
Коэффициент трения f; 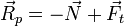 — асимметричная реакция опорной поверхности, векторная сумма вертикальной
— асимметричная реакция опорной поверхности, векторная сумма вертикальной 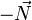 и горизонтальной
и горизонтальной 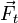 компонент;
компонент; 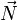 — прижимающая сила;
— прижимающая сила; 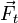 — сила трения качения.
— сила трения качения.
Коэффициент трения качения имеет следующие физические интерпретации:
· Если тело находится в покое и внешняя сила отсутствует, то реакция опоры лежит на той же линии, что и прижимающая сила. Когда тело катится, то из условия равновесия следует, что нормальная составляющая реакции опоры параллельна и противонаправлена прижимающей силе, но не лежит с ней на одной линии. Коэффициент трения качения равен расстоянию между прямыми, вдоль которых действуют прижимающая сила и нормальная составляющая реакции опоры
· Движение катящегося тела без проскальзывания можно рассматривать как поворот вокруг мгновенной оси вращения (на рис. 4 — точка приложения вектора 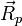 ), которая для абсолютно твёрдых тел совпадает с основанием перпендикуляра, опущенного из центра круга на опору. Для случая реальных (деформирующихся под нагрузкой) материалов мгновенный центр вращения смещён в направлении качения тела, а величина смещения равна значению коэффициента трения качения.
), которая для абсолютно твёрдых тел совпадает с основанием перпендикуляра, опущенного из центра круга на опору. Для случая реальных (деформирующихся под нагрузкой) материалов мгновенный центр вращения смещён в направлении качения тела, а величина смещения равна значению коэффициента трения качения.
 16) Равнодействующая
16) Равнодействующая 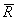 двух параллельных сил, направленных в одну сторону, параллельна этим силам и направлена в ту же сторону; модуль равнодействующей равен сумме модулей данных сил, а линия действия равнодействующей делит расстояние между точками приложения данных сил внутренним образом на части, обратно пропорциональные модулям этих сил, т.е.
двух параллельных сил, направленных в одну сторону, параллельна этим силам и направлена в ту же сторону; модуль равнодействующей равен сумме модулей данных сил, а линия действия равнодействующей делит расстояние между точками приложения данных сил внутренним образом на части, обратно пропорциональные модулям этих сил, т.е.
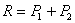 ;
; 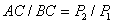 .
.
Используя известное свойство пропорции, можно получить
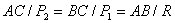 .
.
Пусть теперь имеем две параллельные силы 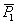 и
и 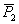 , приложенные в точках
, приложенные в точках 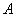 и
и 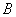 и направленные в противоположные стороны; такие силы называются антипараллельными.
и направленные в противоположные стороны; такие силы называются антипараллельными.

Предположим, что 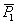 >
> 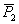 . Равнодействующая
. Равнодействующая 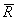 двух антипараллельных сил параллельна этим силам и направлена в сторону большей силы; модуль равнодействующей равен разности модулей данных сил, а линия ее действия делит расстояние между точками приложения данных сил внешним образом на части, обратно пропорциональные модулям этих сил, т.е.
двух антипараллельных сил параллельна этим силам и направлена в сторону большей силы; модуль равнодействующей равен разности модулей данных сил, а линия ее действия делит расстояние между точками приложения данных сил внешним образом на части, обратно пропорциональные модулям этих сил, т.е.
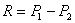 ;
; 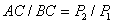 и
и 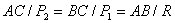 .
.
Как видно, в этом случае линия действия равнодействующей 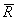 проходит через точку, лежащую вне отрезка
проходит через точку, лежащую вне отрезка 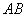 , и притом ближе к большей силе.
, и притом ближе к большей силе.

Рассмотрим систему параллельных сил 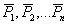 , приложенных в точках
, приложенных в точках 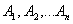 , приводящуюся к равнодействующей
, приводящуюся к равнодействующей 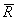 , приложенной в точке
, приложенной в точке 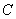
Положение центра параллельных сил 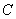 определится его радиусом-вектором
определится его радиусом-вектором 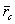 относительно начала координат
относительно начала координат 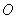 или тремя координатами
или тремя координатами 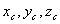 . Положение точки приложения каждой силы
. Положение точки приложения каждой силы 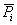 определяется радиусом-вектором
определяется радиусом-вектором 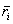 или координатами
или координатами 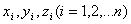 .
.
Опуская выкладки, приведем формулу, определяющую радиус-вектор центра параллельных сил
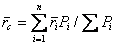 . (10)
. (10)
Спроектировав равенство (5) на оси координат, получим формулы для определения координат центра параллельных сил
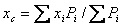 ;
;  ;
; 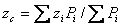 . (11)
. (11)
В формулах (11) координаты 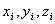 и значения сил
и значения сил 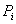 являются алгебраическими величинами. Заметим, что выбор направления, вдоль которого параллельные силы считаются положительными, произволен и на результатах вычисления координат по формулам (11) не отражается.
являются алгебраическими величинами. Заметим, что выбор направления, вдоль которого параллельные силы считаются положительными, произволен и на результатах вычисления координат по формулам (11) не отражается.
17) Центр тяжести
Представим себе какое-нибудь твердое тело, находящееся близ поверхности Земли (рис.1). Силы притяжения 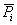 отдельных частиц тела к Земле направлены приблизительно к центру Земли. Так как размеры рассматриваемых тел малы по сравнению с радиусом Земли, то эти силы можно считать параллельными. Центр
отдельных частиц тела к Земле направлены приблизительно к центру Земли. Так как размеры рассматриваемых тел малы по сравнению с радиусом Земли, то эти силы можно считать параллельными. Центр 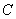 этой системы параллельных сил называется центром тяжести данного тела, а равнодействующая этих сил
этой системы параллельных сил называется центром тяжести данного тела, а равнодействующая этих сил 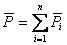 , проходящая через точку
, проходящая через точку 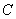 , представляет собой вес этого тела.
, представляет собой вес этого тела.

Так как центр тяжести тела есть центр параллельных сил, то для вычисления координат центра тяжести тела можно воспользоваться формулами, приведенными в предыдущем модуле
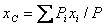 ,
, 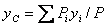 ,
, 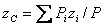 (16)
(16)
где 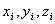 - координаты любой частицы твердого тела.
- координаты любой частицы твердого тела.
Заметим, что в (16) алгебраическими величинами являются только координаты точек, а значения 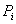 всегда положительны, так как все силы направлены в одну сторону.
всегда положительны, так как все силы направлены в одну сторону.
Обозначим объемы элементарных частиц через 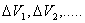 , а вес единицы объема тела через
, а вес единицы объема тела через 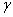 . Если тело однородно, то получим
. Если тело однородно, то получим
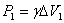 ,
, 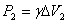 ,……
,……
Подставив эти значения сил 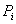 в формулы (2), будем иметь
в формулы (2), будем иметь
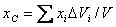 ,
, 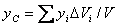 ,
, 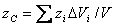 , (17)
, (17)
где 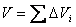 - объем всего тела.
- объем всего тела.
Для получения точных формул координат центра тяжести однородного тела, нужно в формулах (17) перейти к пределу, полагая, что число элементарных частиц неограниченно возрастает, а объем 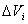 каждой частицы стремится к нулю
каждой частицы стремится к нулю
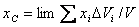 ,
, 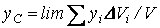 ,
, 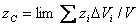 . (18)
. (18)
Если имеем однородное тело, имеющее форму тонкой пластинки, то его можно рассматривать как материальную плоскую фигуру, положение центра тяжести которой определяется двумя координатами 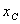 и
и 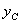 (рис.2).
(рис.2).

В этом случае вместо элементов объема 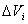 нужно брать элементы площади
нужно брать элементы площади 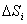 , а в знаменателе вместо
, а в знаменателе вместо 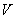 - площадь
- площадь 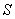 данной фигуры. Следовательно, для координат центра тяжести плоской фигуры будем иметь
данной фигуры. Следовательно, для координат центра тяжести плоской фигуры будем иметь
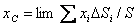 ,
, 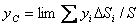 . (19)
. (19)
Аналогично, для координат центра тяжести однородной плоской материальной линии 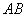 (например, тонкой проволоки, согнутой в виде плоской кривой), получим
(например, тонкой проволоки, согнутой в виде плоской кривой), получим

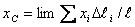 ,
, 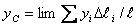 , (20)
, (20)
где 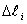 - длина элементарной дуги данной линии, а
- длина элементарной дуги данной линии, а 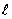 - вся длина этой линии (рис.3).
- вся длина этой линии (рис.3).
Следует отметить, что центр тяжести 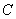 кривой линии вообще не лежит на этой линии. Вычисление пределов сумм, входящих в полученные формулы (18), (19) и (20), производится в общем случае методами интегрального исчисления; эти пределы выражаются определенными интегралами, распространенными соответственно на весь объем тела или на всю площадь фигуры или же взятыми вдоль данной линии.
кривой линии вообще не лежит на этой линии. Вычисление пределов сумм, входящих в полученные формулы (18), (19) и (20), производится в общем случае методами интегрального исчисления; эти пределы выражаются определенными интегралами, распространенными соответственно на весь объем тела или на всю площадь фигуры или же взятыми вдоль данной линии.
18) Способы определения положения центров тяжести тел. Способ группировки. Центр тяжести. Приведем вспомогательную теорему для определения положения центра тяжести: если однородное тело имеет плоскость, или ось, или центр симметрии, то центр тяжести такого тела лежит соответственно в этой плоскости, на этой оси или в этом центре симметрии.
 Теперь перейдем к определению положения центра тяжести плоской фигуры сложной формы. Пусть требуется определить положение центра тяжести плоской фигуры, состоящей из трех частей, положение центров тяжести которых известно (рис1).
Теперь перейдем к определению положения центра тяжести плоской фигуры сложной формы. Пусть требуется определить положение центра тяжести плоской фигуры, состоящей из трех частей, положение центров тяжести которых известно (рис1).
Положим, что площади частей фигуры соответственно равны 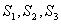 , а координаты их центров тяжести
, а координаты их центров тяжести 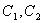 и
и 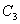 будут
будут 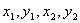 и
и 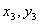 . Тогда координаты ее центра тяжести
. Тогда координаты ее центра тяжести 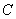 определятся формулами
определятся формулами
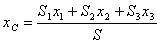 ;
; 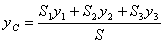 . (21)
. (21)
 Этими формулами удобно пользоваться и при определении положения центра тяжести плоской фигуры, из которой вырезана некоторая часть (рис.2).
Этими формулами удобно пользоваться и при определении положения центра тяжести плоской фигуры, из которой вырезана некоторая часть (рис.2).
В этом случае координаты центра тяжести выражаются формулами
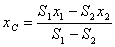 ,
, 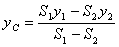 , (22)
, (22)
где 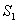 и
и 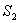 - площади соответственно всей фигуры и вырезанной из нее части, а
- площади соответственно всей фигуры и вырезанной из нее части, а 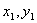 и
и 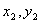 - координаты их центров тяжести.
- координаты их центров тяжести.
Этот способ определения центра тяжести плоской фигуры называется способом отрицательных площадей.
 В заключении приведем формулы для определения положения центров тяжести некоторых фигур.
В заключении приведем формулы для определения положения центров тяжести некоторых фигур.
а) Центр тяжести площади треугольника
Центр тяжести 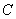 площади треугольника совпадает с точкой пересечения его медиан
площади треугольника совпадает с точкой пересечения его медиан 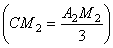 .
.
Если обозначить координаты вершин данного треугольника через ( 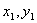 ), (
), ( 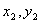 ), (
), ( 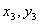 ), то для координат
), то для координат 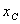 и
и 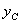 его центра тяжести получим
его центра тяжести получим

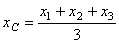 ,
, 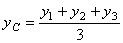 . (23)
. (23)
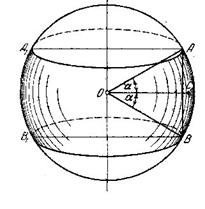
б) Центр тяжести дуги окружности (дуга  )
)
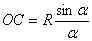 (24)
(24)
где 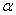 - половина центрального угла дуги
- половина центрального угла дуги 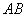 , измеряемого в радианах.
, измеряемого в радианах.
в) Центр тяжести площади кругового сектора ( 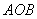 )
)

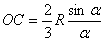 (25)
(25)
 19) Движение точки может быть задано тремя способами: естественным, векторным и координатным.
19) Движение точки может быть задано тремя способами: естественным, векторным и координатным.
При векторном способе задания движения точки положение точки 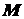 определяется величиной и направл<
определяется величиной и направл<
