Модуль 9.Корреляционный и регрессионный анализы

1. Какие задачи решаются в корреляционном анализе?

2. Может ли статистическая оценка коэффициента линейной корреляции принимать значения, модуль которых будет больше единицы?

3. В каком случае условные распределения компонент случайного вектора будут совпадать с частными распределениями компонент?

4. Какой вид будут иметь функции регрессии каждой из компонент случайного вектора, если эти компоненты – независимые случайныевеличины?

5. Определите координаты точки пересечения линейных уравнений регрессии компонент двумерной случайной величины.

6. При каком условии на компоненты двумерной случайной величины функции линейной регрессии одной компоненты на другую будут тождественно совпадать?

7. Чему будут равны остаточные дисперсии компонент двумерной случайной величины, если эти компоненты будут независимыми?

8. Чему будут равны остаточные дисперсии компонент двумерной случайной величины, если эти компоненты будут связаны линейной функциональной зависимостью?

9. Какой критерий применяется при проверке значимости коэффициента линейной корреляции?

10. В чём заключается различие между корреляционным и регрессионным анализами?

.

IV.Методические указания

Модуль 1. Вероятностное пространство с не более чем счетным множеством элементарных исходов

Цель модуля: Студент должен ознакомиться с основными понятиями и определениями теории вероятностей. Научиться решать задачи определения вероятностей наступления событий для простейших моделей испытаний, предусматривающих построение не более чем счётного множества элементарных исходов.

Введение основных понятий теории вероятностей, базируется на договоре о существе содержания терминов, на которых базируется новый предмет. Это понятия: испытание, элементарный исход, множество элементарных исходов, благоприятствующие элементарные исходы, равновозможные элементарные исходы. Усвоение этих основных понятий обеспечивается только жизненным опытом и способностью к абстрактному мышлению.

После ознакомления с основными понятиями, формулируется первые основные определения теории вероятностей. Это определения случайного события, противоположного события, достоверного и невозможного события, суммы и произведения событий, совместных и несовместных событий, алгебры событий.

После ознакомленияс основными понятиям и усвоения основныхе определений, проводится подготовка к знакомству с новым, важнейшим понятием курса – понятием вероятности случайного события. Делается это аксиоматически, путем введения вероятностной функции Р.

Вероятностная функцияPвводится следующим образом.

Сначала постулируется, аксиоматически формулируется: «Каждому элементарному исходу некоторым разумным способом ставим в соответствие положительное число , (записывается это так: ). При этом требуется, чтобы выполнялось условие: .» Затем, с использованием понятия благоприятствующего случайному событию элементарного исхода, определяется вероятность наступления случайного события следующим образом: . То есть, по существу, каждому элементу A алгебрыA,A 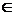A,ставится в соответствие неотрицательное число, которое называется вероятностью этого элемента– вероятностью наступления случайного события A. То есть вводится функция, которая отображаетмножество Aво множество чисел сегмента . Кратко это можно записать так: P:A . Так как здесь нельзя, подобно тому как это делается в анализе, ввести вероятностную функцию Р с помощью аналитической записи типа : , то у студента на этом этапе изучения курса возникают трудности в осмыслении понятия вероятностная функция.

Для облегченияпроцесса пониманиятермина «вероятность случайного события», мыприбегаем к механической интерпретации. Установление соответствия интерпретируется как распределение по элементам множества Wнекоторым разумным способом единичной массы: в каждом мы “помещаем” массу равную . Вероятность случайного событияA теперь понимается какдоля единичной массы, оказавшейся над подмножеством А множества W.

Слова «некоторым разумным способом устанавливаем соответствие » своей неопределенностью вносят дополнительные трудности в понятие термина «введение вероятностной функции» и нуждаются в пояснениях. Эти пояснения даются путемрассмотрения трёх моделей, трёх конкретных типов испытаний, в которых это соответствие устанавливается вполне естественным, разумным способом.

Классическая модель, основанная на понятии «испытаний с равновозможными элементарными исходами», позволяет установить соответствие так: .

Биномиальная модель, основанная на понятии «серии повторных независимых испытаний», позволяет установить соответствие так: .

Геометрическая модель, основанная на понятии «последовательность повторных независимых испытаний до первого положительного исхода», позволяет установить соответствие так: .

Перед рассмотрением биномиальной модели сначала вводится понятие «случайного события B наступившего при условии, что экспериментатору известно, что событие A уже произошло» и формулируется определение условной вероятности . Затем рассматривается вероятность произведения событий и формулируется одно из фундаментальных определений теории – определение независимости событий.

Свойства вероятностной функции, а так же формулы полной вероятности и Байеса являются теоремами и следствиями, вытекающимииз аксиоматического введения вероятностной функции P, и позволяют решать на практических занятиях довольно широкий круг задач.

Модуль 2. Построение общей вероятностной модели