Осн типы событий.Алгебра событий.
Два события А и В называются несовместными, если наступление одного исключает появление другого. (Пример: соб.А – студент получил 5 на экзамене, соб.В – этот же студент получил 4 по этому же предмету. Соб.А и В несовместные, т.к. не могут произойти при одном исходе испытаний.)
Два события А и В называются совместными, если они могут произойти при одном исходе испытаний. (Студент получил 5 по одному предмету и 4 по другому)
Событие наз-ся достоверным, если в результате испытания оно обязательно должно произойти.
Событие наз-ся невозможным, если в результате испытания оно вообще не может произойти. (Пример: в партии изделия все стандартные. Соб.А – извлечение стандартного изделия, соб.В – извлечение брака. А – достоверное, В – невозможное)
События называются равновозможными, если в результате испытания по условиям симметрии не одно из этих событий не является объективно более возможным.(Пример: пусть происходит подбрасывание монеты. Соб.А- орел, соб.В – решка)
Несколько событий называются единственно возможными, если в результате испытания обязательно должно произойти хотя бы одно из них.
События образуют полную группу, если они являются единственно возможными и несовместными исходами испытания.
Два несовместных события, из которых одно должно произойти называются противоположными.
Соб. А1 и А2нзвравными, если осуществление соб.А1 влечет за собой осуществление соб. А2 и наоборот.А1=А2
Суммой (объединением) соб. А и Bнзв соб.C, к-рое означает осущ-е хотя бы одного из соб. А или B. 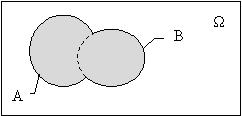 Произведением (пересечением) соб. А и Bнзв соб. C, к-рое означает, что одновременно осущ-ся и А и B.
Произведением (пересечением) соб. А и Bнзв соб. C, к-рое означает, что одновременно осущ-ся и А и B. 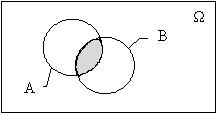 Разностью соб. А и Bнзв соб. C, к-рое означает, что происх. соб. А, но не происх. соб. B.
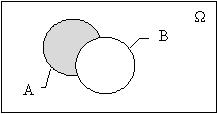
Разностью соб. А и Bнзв соб. C, к-рое означает, что происх. соб. А, но не происх. соб. B.
 Соб. Ā нзвпротивоположным по отношению к соб. А, если оно состоит из элемент.соб., не входящих в соб.А, но входящих в простр-во элемент.соб. Ω.
Соб. Ā нзвпротивоположным по отношению к соб. А, если оно состоит из элемент.соб., не входящих в соб.А, но входящих в простр-во элемент.соб. Ω. 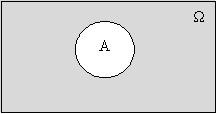
Ā=Ω\А,А+Ā=Ω
Несовместные события:
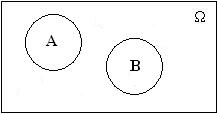
А∙B=Ø
Свойства операций:
1.Ω+А=Ω2.Ω∙А=А
3.А∙А=А4.А+Ø=А
5.А∙Ø=Ø6.(А\В)∙(В\А)=Ø
7.А+Ā=Ω8.А∙Ā=Ø
9. 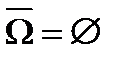 10.
10. 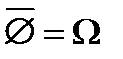
11. 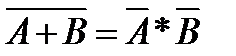 12.
12. 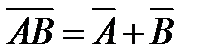
13.А+В=В+А 14.А∙В=В∙А
15.(А+В)+С=А+(В+С) 16.(А∙В)∙С=А∙(В∙С)
17.С(А+В)=СА+СВ 18.А+ВС=(А+В)(А+С)
Теорема сложения вер-тей.
Т-ма сложения вер-тей несовместных событий.
«Вер-ть суммы несовместных событий равна сумме вер-тей этих событий»
Р(А + В + …k) = Р(А) + Р(В) + …+ P(k), где А, В, …, k – несовместные.
Док-во.(сумма двух событий) Пусть в результате испытаний из общ числа n равновозможных и несовместных исходов испытаний А благоприятствует m1 случаев, а В – m2 случаев. Тогда вер-ть события А (по классич. опр.) равна m1/n, а
Р(В) = m2/n , т.к. события А и В несовместные, то ни один из случаев благоприятствующий событию А, не благоприятствует событию В, след. (А+В) благоприятствует (m1+m2) случая, след-но
Р(А+В) = (m1+m2)/n = m1/n + m2/n = P(A)+P(B)
Следствие 1:Сумма вер-тей событий, образующих полную группу равна 1.
Следствие 2:Сумма вер-тей противоположных событий так же равна 1.
