Классического вариационного исчисления
2.1. Уравнения движения системы материальных точек
Основным вариационным принципом в механике является принцип стационарного действия Остроградского-Гамильтона (принцип наименьшего действия): среди возможных, т.е. совместимых со связями, движений системы материальных точек в действительности осуществляется движение, дающее стационарное значение (минимум) интегралу, называемому действием по Лагранжу
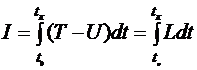 , (2.1)
, (2.1)
где 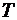 - кинетическая, а
- кинетическая, а 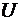 - потенциальная энергия системы,
- потенциальная энергия системы, 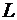 - функция Лагранжа.
- функция Лагранжа.
Рассмотрим систему 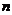 свободных материальных точек с массами
свободных материальных точек с массами 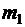 ,
, 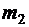 , …,
, …, 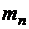 с координатами
с координатами 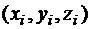 ,
, 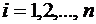 . Кинетическая энергия системы равна
. Кинетическая энергия системы равна
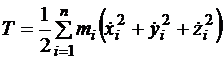 . (2.2)
. (2.2)
Предположим, что система обладает потенциальной энергией, т.е. существует функция 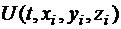 , определяющая компоненты сил следующим образом:
, определяющая компоненты сил следующим образом:
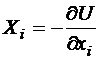 ,
, 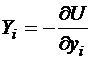 ,
, 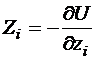 .
.
Если функционал (2.1) достигает экстремума (минимума), то справедливы уравнения Эйлера:
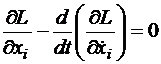 ,
,
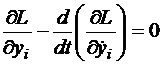 , (2.3)
, (2.3)
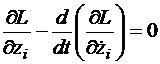 .
.
Учитывая, что 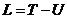 , получим
, получим
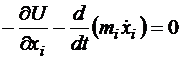 ,
,
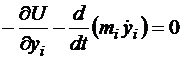 ,
,
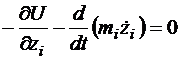 .
.
Из этих уравнений следуют уравнения движения системы 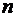 материальных точек
материальных точек
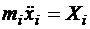 ,
, 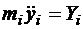 ,
, 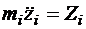 ,
, 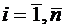 . (2.4)
. (2.4)
2.2. Закон сохранения энергии в консервативной системе
Для функционала
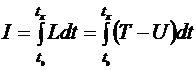
сопряженные переменные (импульсы) и функция Гамильтона записываются следующим образом:
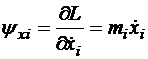 ,
,
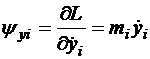 , (2.5)
, (2.5)
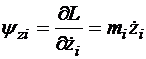 ,
,
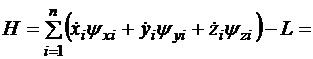
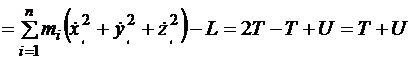 . (2.6)
. (2.6)
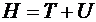 - полная энергия системы. Если рассматриваемая система консервативна (т.е.
- полная энергия системы. Если рассматриваемая система консервативна (т.е. 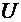 явно не зависит от времени), то
явно не зависит от времени), то 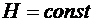 вдоль каждой экстремали. Это означает, что полная энергия консервативной системы постоянна (закон сохранения энергии).
вдоль каждой экстремали. Это означает, что полная энергия консервативной системы постоянна (закон сохранения энергии).
2.3. Задача об оптимальном выведении спутника на орбиту
Рассмотрим задачу выведения спутника на околоземную орбиту с минимальными затратами топлива, т.е. задачу с функционалом
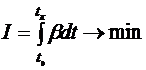 , (2.7)
, (2.7)
где 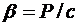 - секундный расход топлива,
- секундный расход топлива, 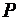 - тяга двигателей,
- тяга двигателей, 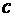 - скорость истечения газов из сопла.
- скорость истечения газов из сопла.
Введем допущения. Будем считать, что двигатели работают без выключений, а их тяга постоянна. В этом случае конечная масса ракеты равна
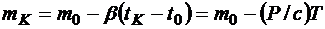 ,
, 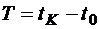 .
.
Параметры 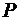 и
и 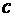 имеют постоянные значения, следовательно, задача о минимальном расходе топлива эквивалентна задаче о минимальном времени выведения, и поэтому функционал (2.7) приводится к виду
имеют постоянные значения, следовательно, задача о минимальном расходе топлива эквивалентна задаче о минимальном времени выведения, и поэтому функционал (2.7) приводится к виду
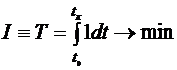 . (2.8)
. (2.8)
Также будем считать, что движение происходит в плоскопараллельном гравитационном поле (сила тяжести постоянна по величине и направлению) при отсутствии сопротивления атмосферы (рис. 2.1). Эти допущения приблизительно соответствуют физической картине движения верхних ступеней ракет-носителей на высотах, превышающих 60…70 км.
При этих допущениях уравнения движения имеют вид
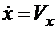 ,
,
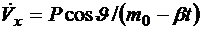 ,
,
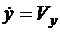 , ... (2.9)
, ... (2.9)
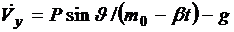 ,
,
Здесь 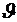 - угол тангажа (угол между продольной осью ракеты и плоскостью местного горизонта).
- угол тангажа (угол между продольной осью ракеты и плоскостью местного горизонта).
Начальные условия интегрирования:
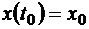 ,
, 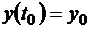 ,
, 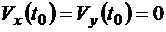 .
.
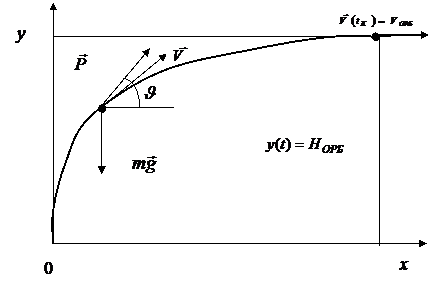
Рис. 2.1. Траектория выведения спутника на орбиту
Имеем задачу на условный экстремум, поскольку кроме функционала есть четыре дифференциальные связи в форме уравнений движения при пяти переменных, описывающих состояние ( 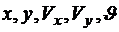 ).
).
Составим расширенный функционал
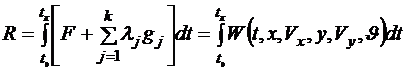 , (2.10)
, (2.10)
где 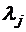 - постоянные множители, а
- постоянные множители, а 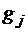 - функции, задающие связи (7.9), и исследуем его на экстремум. Вспомогательная функция
- функции, задающие связи (7.9), и исследуем его на экстремум. Вспомогательная функция  имеет вид
имеет вид
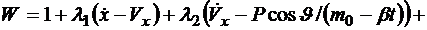
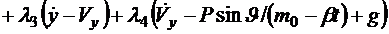 . (2.11)
. (2.11)
Запишем систему уравнений Эйлера
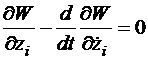 ,
, 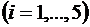 ,
,
где
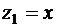 ,
, 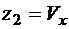 ,
,
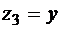 ,
, 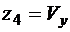 ,
, 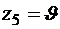 .
.
В скалярном виде:
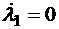 ,
, 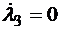 ,
,
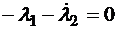 , (2.12)
, (2.12)
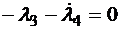 ,
,
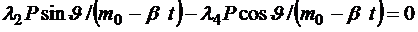 .
.
Отсюда
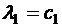 ,
,
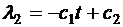 ,
,
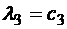 ,
,
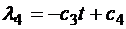 ,
,
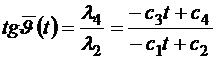 , (2.12)
, (2.12)
где 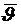 - закон управления углом тангажа, обеспечивающий экстремум
- закон управления углом тангажа, обеспечивающий экстремум 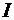 .
.
Следовательно, угол тангажа должен изменяться по закону дробно-линейного тангенса. Оптимальная траектория выведения получается в результате интегрирования уравнений движения с полученным законом изменения тангажа.
Закон изменения угла тангажа содержит четыре константы, однако только три из них являются независимыми, т.к. выражения в числителе и знаменателе допускают деление на любую из постоянных, например, на 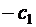 , тогда
, тогда
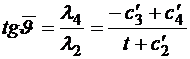 . (2.13)
. (2.13)
С другой стороны, на правом конце траектории имеется четыре граничных условия:
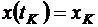 ,
, 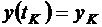 ,
,
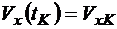 ,
, 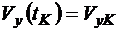 .
.
Поэтому, строго говоря, управляя только углом тангажа, то есть ориентацией ракеты в пространстве, нельзя добиться необходимого значения конечной скорости. Поэтому в число подбираемых параметров приходится включать тягу  , точнее, тяговооруженность верхней ступени ракеты
, точнее, тяговооруженность верхней ступени ракеты 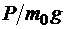 .
.
Рассмотрим два частных случая. Получим закон изменения угла тангажа при выведении спутника ракетой-носителем. В этой задаче в конце траектории не фиксируется координата 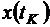 . Из общей формулы для вариации функционала в задаче со свободными концами для нашего случая имеем:
. Из общей формулы для вариации функционала в задаче со свободными концами для нашего случая имеем:
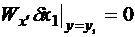 .
.
Учитывая ранее полученные результаты, имеем
 .
.
Тогда 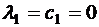 и, следовательно,
и, следовательно,
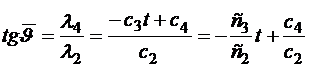 . (2.14)
. (2.14)
Это закон линейного тангенса, который используется в реальных системах управления ракет-носителей. Минимизация расхода топлива на выведение при заданной стартовой массе соответствует максимизации полезной нагрузки, выводимой на орбиту.
Получим закон управления движением баллистической ракеты. В этой задаче в целях упрощения закона управления считают незаданными 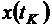 и
и 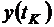 .
.
Тогда
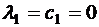 ,
, 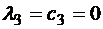 ,
,
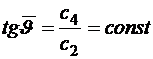 . (2.15)
. (2.15)
Это закон постоянного угла тангажа, используемый в системах управления баллистических ракет. Он обеспечивает достижение заданной конечной скорости при минимальном расходе топлива.
Значения скоростей и координат на оптимальной траектории определяется путем интегрирования уравнений движения (2.9), замкнутых оптимальными законами 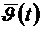 .
.
Практическое занятие № 3
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ
ПРИНЦИПА МАКСИМУМА
3.1. Задача синтеза оптимального управления при переориентации космического аппарата
Рассмотрим задачу одноосной переориентации КА (рис. 3.1).
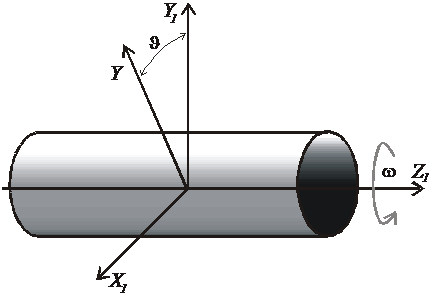
Рис. 3.1. Одноосная переориентация космического аппарата
Здесь OX1, OY1, OZ1 – связанные с корпусом КА оси координат; вращение происходит только вокруг оси OZ1. Уравнения вращательного движения относительно оси OZ1 имеют вид
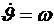 ,
, 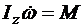 , (3.1)
, (3.1)
где 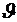 и
и 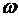 - угол и угловая скорость поворота вокруг оси
- угол и угловая скорость поворота вокруг оси 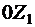 ,
, 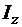 - момент инерции КА относительно оси
- момент инерции КА относительно оси 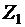 ,
, 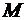 - управляющий момент.
- управляющий момент.
В качестве управления примем угловое ускорение: 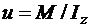 ,
, 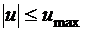 . Тогда уравнения движения примут вид
. Тогда уравнения движения примут вид
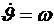 ,
, 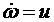 . (3.2)
. (3.2)
Сформулируем оптимизационную задачу. Для данной системы дифференциальных уравнений, описывающих движение КА относительно оси 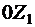 , найти закон управления угловым ускорением, обеспечивающий переориентацию КА из произвольных начальных условий
, найти закон управления угловым ускорением, обеспечивающий переориентацию КА из произвольных начальных условий 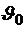 ,
, 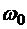 в заданное конечное положение
в заданное конечное положение 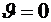 ,
, 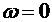 за минимальное время, то есть закон управления
за минимальное время, то есть закон управления 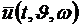 доставляющий минимум функционалу
доставляющий минимум функционалу
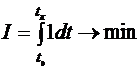 . (3.3)
. (3.3)
Применим алгоритм принципа максимума. Составим гамильтониан
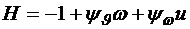 (3.4)
(3.4)
и запишем уравнения для сопряженных переменных
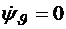 ,
, 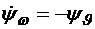 . (3.5)
. (3.5)
Интегрируя эти уравнения, получаем 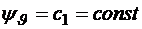 ,
, 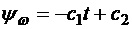 .
.
Так как на управление наложено ограничение, то максимум гамильтониана обеспечивается при максимальном управляющем воздействии: 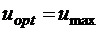 при
при 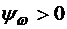 и
и 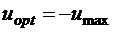 при
при 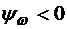 или
или
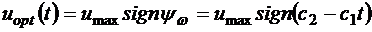 . (3.6)
. (3.6)
Так как 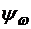 - линейная функция, закон управления будет иметь не больше одного переключения на отрезке
- линейная функция, закон управления будет иметь не больше одного переключения на отрезке 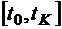 , что полностью соответствует теореме А.А. Фельдбаума для сопряженной системы (3.5).
, что полностью соответствует теореме А.А. Фельдбаума для сопряженной системы (3.5).
Исследуем процесс оптимальной переориентации, изобразив его на фазовой плоскости, т.е. в координатах 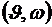 . Проинтегрировав уравнения движения, получим
. Проинтегрировав уравнения движения, получим
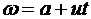 ,
,
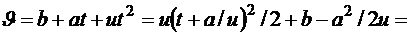 (3.7)
(3.7)
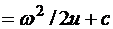 ,
,
где 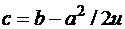 ,
,  и
и 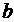 - произвольные постоянные. Управление
- произвольные постоянные. Управление 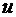 может принимать только два значения:
может принимать только два значения: 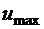 или
или  .
.
Следовательно, оптимальная фазовая траектория – парабола, а движение по фазовой плоскости осуществляется снизу вверх при 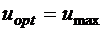 или сверху вниз при
или сверху вниз при 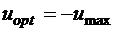 (рис. 3.2). В начало координат ведет только одна траектория, поэтому решение единственно. Эта траектория (линия АОВ) является линией переключения.
(рис. 3.2). В начало координат ведет только одна траектория, поэтому решение единственно. Эта траектория (линия АОВ) является линией переключения.
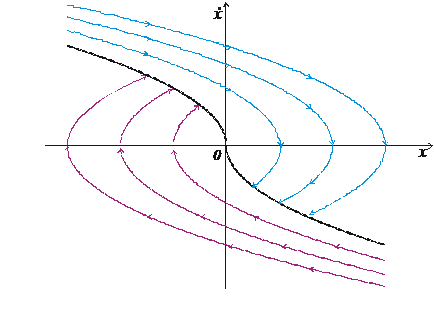
Рис. 3.2. Движение по фазовой плоскости
Получим закон оптимального управления в форме синтеза, то есть зависимости 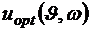 . Имеем для точек, лежащих ниже линии переключения и на дуге ОВ,
. Имеем для точек, лежащих ниже линии переключения и на дуге ОВ, 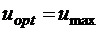 , для точек, лежащих выше линии переключения и на дуге ОА,
, для точек, лежащих выше линии переключения и на дуге ОА, 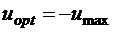 , или
, или
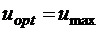 , если
, если 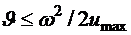 и
и 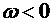 ,
,
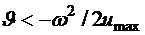 и
и 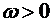 ;
;
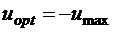 , если
, если 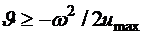 и
и 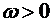 ,
,
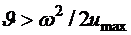 и
и 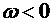 .
.
Оптимальный закон управления в форме синтеза имеет вид
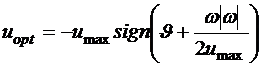 . (3.8)
. (3.8)
3.2. Задача об оптимальном перелете КА с идеально регулируемым двигателем малой тяги
Рассмотрим движение космического аппарата (КА) на достаточном удалении от центров притяжения, таком, что влиянием гравитационных сил можно пренебречь. Такая модель иногда называется моделью «бессилового поля». КА оснащен так называемым идеально регулируемым двигателем малой тяги – электрореактивным двигателем (реактивная струя состоит их заряженных частиц – ионов и электронов, разгоняемых до больших скоростей электромагнитным полем) с глубоким регулированием величины тяги (реактивного ускорения). Критерием оптимальности для КА с подобными двигательными установками служит интеграл от квадрата реактивного ускорения:
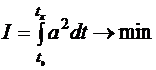 . (3.9)
. (3.9)
Будем считать, что полет КА при отсутствии сил тяготения осуществляется по прямолинейной траектории, соединяющей точки 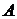 (начальную) и
(начальную) и 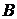 (конечную), как показано на рис. 3.3.
(конечную), как показано на рис. 3.3.
Кинематические параметры движения в момент 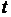 (точка М): вектор положения
(точка М): вектор положения 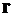 и вектор скорости
и вектор скорости 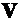 . Векторные уравнения движения (дифференциальные связи) имеют вид:
. Векторные уравнения движения (дифференциальные связи) имеют вид:
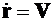 ,
, 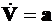 . (3.10)
. (3.10)
или
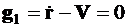 ,
,
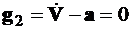 . (3.11)
. (3.11)
Граничные условия задачи
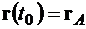 ,
, 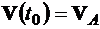 ,
,
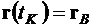 ,
, 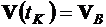 .
.
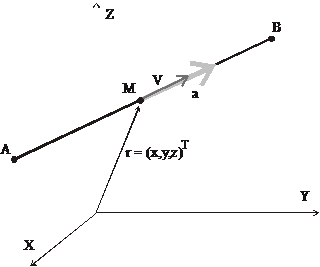
Рис. 3.3. Траектория движения КА в бессиловом поле
Здесь 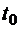 ,
, 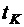 - заданные величины. Получаем задачу на условный экстремум. Переменные, подлежащие определению:
- заданные величины. Получаем задачу на условный экстремум. Переменные, подлежащие определению: 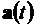 ,
, 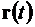 ,
, 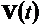 .
.
Запишем расширенный функционал
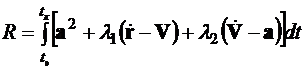 , (3.12)
, (3.12)
где 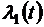 ,
, 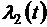 - неизвестные функции. Составим систему уравнений Эйлера для переменных
- неизвестные функции. Составим систему уравнений Эйлера для переменных 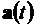 ,
, 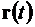 ,
, 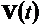 :
:
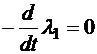 ,
,
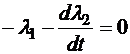 , (3.13)
, (3.13)
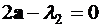 .
.
Из этих уравнений находим
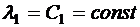 ,
,
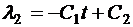 , (3.14)
, (3.14)
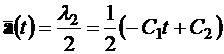 .
.
Оптимальный закон изменения реактивного ускорения имеет вид линейной зависимости от времени. Соответственно, величина ускорения может возрастать, убывать или оставаться постоянной. Это зависит от граничных условий задачи. Изменение 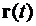 ,
, 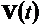 вдоль траектории получаем путем интегрирования:
вдоль траектории получаем путем интегрирования:
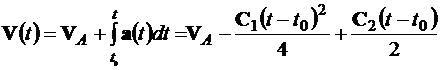 (3.15)
(3.15)
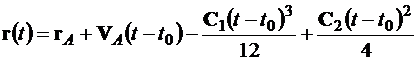 . (3.16)
. (3.16)
Векторные константы 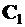 и
и 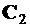 определяются из граничных условий задачи.
определяются из граничных условий задачи.
3.3. Задача о минимуме времени разгона космического аппарата с малой тягой до параболической скорости
Пусть космический аппарат (КА) стартует с начальной круговой орбиты и совершает разгон в центральном поле тяготения под действием малой тяги 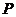 постоянной величины:
постоянной величины: 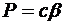 , где
, где 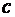 - скорость истечения,
- скорость истечения, 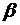 - секундный расход массы. Следовательно, секундный расход массы определяется по формуле:
- секундный расход массы. Следовательно, секундный расход массы определяется по формуле: 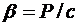 . С другой стороны,
. С другой стороны, 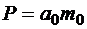 , где
, где 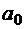 - начальной ускорение, а
- начальной ускорение, а 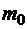 - начальная масса КА. Запишем выражение для текущего значения ускорения:
- начальная масса КА. Запишем выражение для текущего значения ускорения:
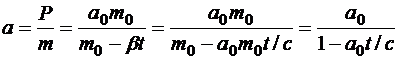 . (3.17)
. (3.17)
Будем считать, что вектор тяги не выходит из плоскости орбиты. Тогда плоское движение КА может быть описано в полярных координатах 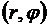 , где
, где 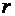 - расстояние до центра притяжения,
- расстояние до центра притяжения, 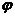 - центральный угол, отсчитываемый от некоторого постоянного направления (рис.3.4).
- центральный угол, отсчитываемый от некоторого постоянного направления (рис.3.4).
Если текущие значения расстояния, скорости и времени отнести соответственно к радиусу начальной орбиты, круговой скорости и времени прохождения одного радиана на этой орбите, то уравнения движения запишутся следующим образом:
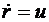 ,
,
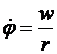 ,
,
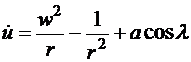 , (3.18)
, (3.18)
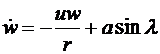 .
.
Здесь 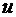 и
и 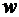 - радиальная и трансверсальная составляющие скорости,
- радиальная и трансверсальная составляющие скорости, 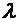 - угол между радиусом-вектором и вектором тяги. На рис. 3.4 обозначен также угол
- угол между радиусом-вектором и вектором тяги. На рис. 3.4 обозначен также угол 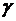 между векторами тяги и скорости.
между векторами тяги и скорости.
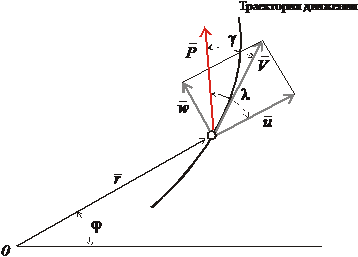
Рис.3.4. Полярные координаты
Сформулируем оптимизационную задачу. Для данной неавтономной системы дифференциальных уравнений, описывающих движение КА с малой тягой, найти закон управления углом  , обеспечивающий минимальное время достижения параболической скорости, т.е. доставляющий минимум функционалу
, обеспечивающий минимальное время достижения параболической скорости, т.е. доставляющий минимум функционалу
 . (3.19)
. (3.19)
В конечный момент времени необходимо достигнуть параболической скорости; при этом удельная механическая энергия поступательного движения центра масс аппарата равна нулю. Запишем граничные условия:
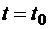 :
: 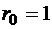 ,
, 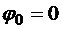 ,
, 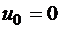 ,
, 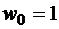 ,
,
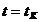 :
: 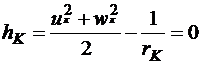 .
.
Последнее условие можно записать так: 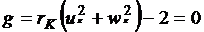 , где
, где 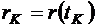 ,
, 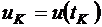 ,
, 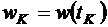 - параметры траектории в точке набора параболической скорости,
- параметры траектории в точке набора параболической скорости, 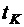 - не задано.
- не задано.
Будем решать задачу на основе принципа максимума Понтрягина. Введем сопряженную вектор-функцию 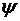 и запишем выражение для гамильтониана:
и запишем выражение для гамильтониана:
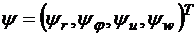 ,
,
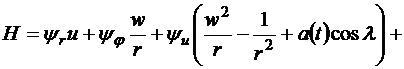 (3.20)
(3.20)
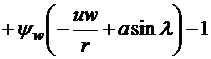 .
.
Неавтономность системы не вносит изменений в алгоритм решения задачи. В соответствии с принципом максимума необходимое условие оптимальности имеет вид
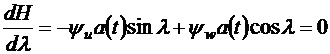 . (3.21)
. (3.21)
Откуда
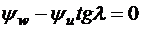 ,
, 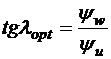
или
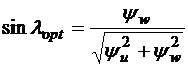 ,
,
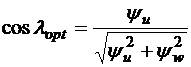 . (3.22)
. (3.22)
Определим знак второй производной
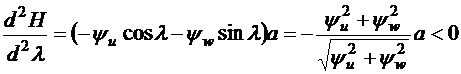 .
.
Следовательно, при таком управлении гамильтониан действительно достигает максимума по управлению 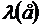 .
.
Сопряженная система уравнений имеет вид
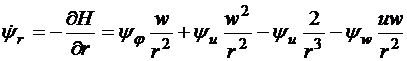 ,
,
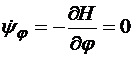 ,
,
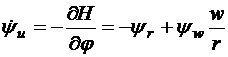 , (3.23)
, (3.23)
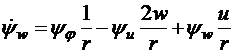 .
.
Запишем условия трансверсальности, учитывая связь между параметрами в конце траектории:
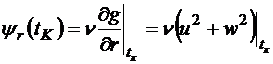 ,
,
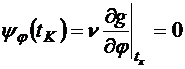 ,
,
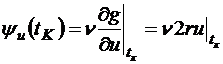 ,
,
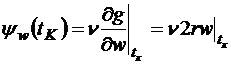 .
.
Из второго условия следует, что 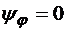 . Кроме того,
. Кроме того,
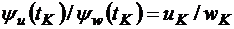 ,
,
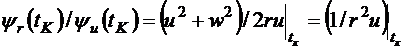 .
.
Откуда
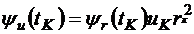 ,
,
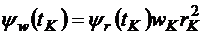 . (3.24)
. (3.24)
Таким образом, имеем два соотношения, которые связывают три сопряженные переменные в конце оптимальной траектории. Третье граничное условие имеет вид
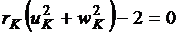 .
.
Полная система уравнений, замкнутая оптимальным законом управления, принимает вид
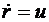 ,
,
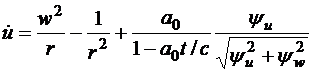 ,
,
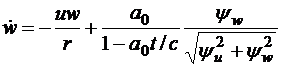 , (3.25)
, (3.25)
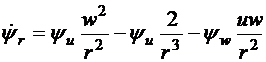 ,
,
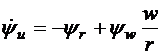 ,
,
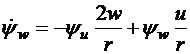 .
.
Для решения краевой задачи необходимо подобрать начальные значения 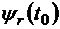 ,
, 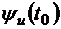 ,
, 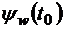 так, чтобы при
так, чтобы при 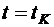 удовлетворить трем условиям трансверсальности:
удовлетворить трем условиям трансверсальности:
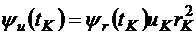 ,
, 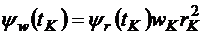 ,
,
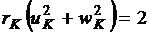 .
.
Последнее условие используется для выхода из интегрирования.
Уравнения сопряженной системы уравнений можно пронормировать по одной из переменных, разделив каждый член, например, на 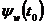 . Тогда
. Тогда
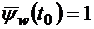 ,
, 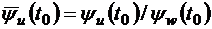 ,
, 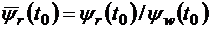 .
.
Таким образом, для выполнения двух условий трансверсальности необходимо подобрать начальные значения двух сопряженных переменных, т.е. решить краевую задачу второго порядка. Выразим их через величины, имеющие простой физический смысл:
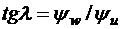 , но
, но 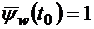 ,
,
поэтому
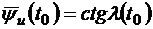 .
.
После преобразования можно получить
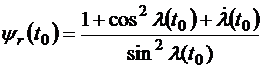 . (3.26)
. (3.26)
Предположив, что в начале разгона угол 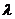 близок к 90
близок к 90  , а скорость его изменения близка к 0, получим
, а скорость его изменения близка к 0, получим
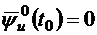 ,
, 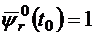 .
.
Из условий трансверсальности следует, что
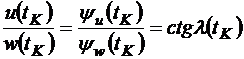 , (3.27)
, (3.27)
т.е. при 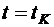 тяга должна быть направлена по скорости.
тяга должна быть направлена по скорости.
Решив краевую задачу, получим оптимальный закон управления направлением вектора тяги. На рис. 3.5 показан вид оптимального управления углом 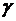 между тягой и вектором скорости.
между тягой и вектором скорости.
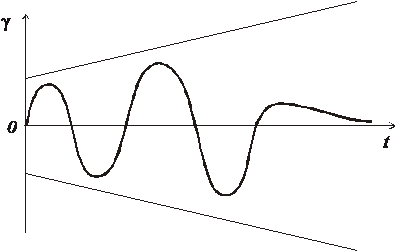
Рис. 3.5. Оптимальное управление углом 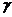
При разгоне КА с малой тягой вектор тяги колеблется относительно вектора скорости с периодом, равным времени обращения по орбите, совпадая с ним в конечный момент при 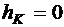 .
.
Практическое занятие № 4
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ
ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
4.1. Выбор оптимальной траектории набора высоты скоростного самолета-перехватчика
Самолет, находящийся в точке А, имеющий скорость 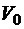 и высоту
и высоту 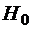 , должен подняться на заданную высоту
, должен подняться на заданную высоту 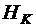 и достигнуть значения скорости
и достигнуть значения скорости 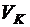 . Пусть известен расход топлива, необходимый для подъема с некоторой высоты
. Пусть известен расход топлива, необходимый для подъема с некоторой высоты 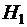 на высоту
на высоту 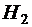 (
( 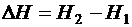 , принимается достаточно малой) при постоянной скорости
, принимается достаточно малой) при постоянной скорости 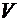 , а также расход топлива, необходимый для разгона со скорости
, а также расход топлива, необходимый для разгона со скорости 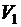 до скорости
до скорости 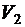 (
( 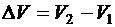 также достаточно мала) при постоянной высоте
также достаточно мала) при постоянной высоте 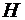 . Это позволяет построить сетку локальных расходов топлива на плоскости параметров
. Это позволяет построить сетку локальных расходов топлива на плоскости параметров 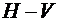 (рис. 4.1). На этой сетке по горизонтали и вертикали отложены расходы топлива в некоторых условных единицах.
(рис. 4.1). На этой сетке по горизонтали и вертикали отложены расходы топлива в некоторых условных единицах.
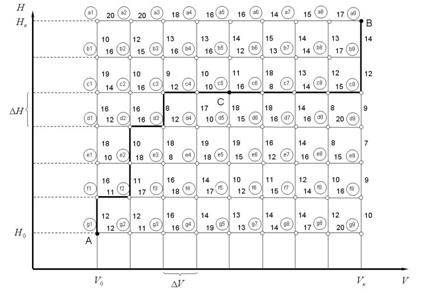
Рис. 4.1. Сетка локальных расходов скорости
Необходимо найти оптимальную траекторию в координатах  , при которой суммарный расход топлива на перемещение из точки А в точку В будет минимальным. Ограничением в данной задаче является условие движения по сетке только вверх и вправо.
, при которой суммарный расход топлива на перемещение из точки А в точку В будет минимальным. Ограничением в данной задаче является условие движения по сетке только вверх и вправо.
Будем решать задачу методом динамического программирования. Согласно принципу оптимальности, попав в промежуточную точку С в результате стратегии управления  , для оптимального перемещения в точку В надо использовать стратегию управления
, для оптимального перемещения в точку В надо использовать стратегию управления  , оптимальную относительно промежуточного состояния в точке С.
, оптимальную относительно промежуточного состояния в точке С.
Введем критерий оптимальности
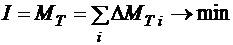 , (4.1)
, (4.1)
где 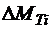 - локальный расход топлива, затрачиваемый на перемещение между соседними узлами сетки, i - номер шага. Общее число шагов может быть произвольным, оно зависит от шага разбиения.
- локальный расход топлива, затрачиваемый на перемещение между соседними узлами сетки, i - номер шага. Общее число шагов может быть произвольным, оно зависит от шага разбиения.
Запишем
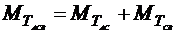 .
.
Функция будущих потерь
 (4.2)
(4.2)
представляет собой минимальное значение критерия на оставшемся участке, представленное в виде зависимости от координат промежуточной точки С.
Основное рекуррентное соотношение записывается так:
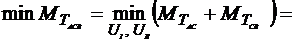
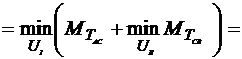
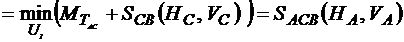 . (4.3)
. (4.3)
На основании соотношения (4.3) будем решать задачу последовательно, двигаясь от точки В к точке А. Обозначим узлы сетки строчными буквами с индексами. На первом шаге процесса возможны только два варианта попадания в точку В из соседних точек 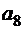 и
и 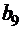 . Сравнить эти варианты невозможно, так как координаты точек
. Сравнить эти варианты невозможно, так как координаты точек 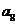 и
и 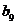 разные. На втором шаге, когда переход в точку В включает две ячейки сетки, возможны уже четыре маршрута (их начальные точки обозначены
разные. На втором шаге, когда переход в точку В включает две ячейки сетки, возможны уже четыре маршрута (их начальные точки обозначены 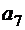 ,
, 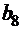 и
и 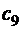 , причем точка
, причем точка 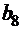 является общей для двух возможных маршрутов). Именно эти два маршрута сравниваются по суммарным затратам топлива, и остается только один, где расход минимален. Другие начальные точки
является общей для двух возможных маршрутов). Именно эти два маршрута сравниваются по суммарным затратам топлива, и остается только один, где расход минимален. Другие начальные точки 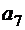 и
и 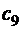 пока остаются в числе возможных точек маршрута. Затем процедура повторяется, на каждом шаге происходит сравнение маршрутов, имеющих одинаковые начальную и конечную точки, и отбрасывание неоптимальных вариантов.
пока остаются в числе возможных точек маршрута. Затем процедура повторяется, на каждом шаге происходит сравнение маршрутов, имеющих одинаковые начальную и конечную точки, и отбрасывание неоптимальных вариантов.
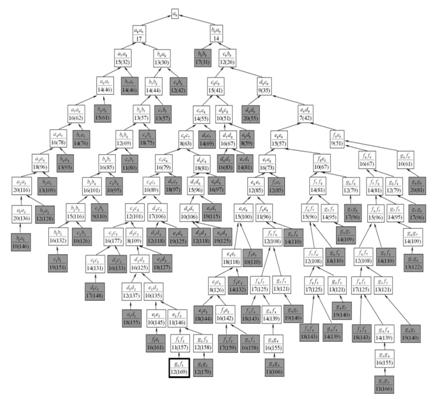
Рис. 4.2. Процесс решения задачи
Процесс решения задачи удобно отобразить в виде расходящегося «веника» (рис. 4.2), на каждом узле которого, начиная со второго, идет исключение неоптимальных маршрутов (выделяются черными квадратами). Постепенно «веник» начинает сужаться, пока не сходится к начальной точке А (результат обведен жирной рамкой).
Оптимальная траектория, полученная на основе такого алгоритма, показана на рис. 7.7. Очевидно, уменьшая шаг разбиения по 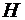 и
и  , можно приблизиться к непрерывному процессу.
, можно приблизиться к непрерывному процессу.
Рис. 4.3. Исходные данные для оптимизации траектории
На рис. 4.3 приведены исходные данные для оптимизации траектории набора высоты самолета-перехватчика. Здесь на плоскости параметров  (
( 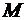 - число Маха, равное отношению скорости полета к скорости звука на данной высоте) нанесены изолинии тангенциальной перегрузки
- число Маха, равное отношению скорости полета к скорости звука на данной высоте) нанесены изолинии тангенциальной перегрузки 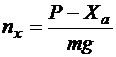 , где
, где  - тяга двигателя на форсажном режиме,
- тяга двигателя на форсажном режиме, 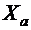 - сила лобового сопротивления,
- сила лобового сопротивления,  - масса самолета,
- масса самолета,  - ускорение силы тяжести.
- ускорение силы тяжести.

Рис. 4.4. Результаты пересчета изолиний тангенциальной перегрузки и оптимальные траектории перехватчика
Здесь же нанесены линии ограничений на допустимые режимы полета: по максимально допустимому коэффициенту подъемной силы 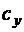 , по предельно допустимому числу Маха
, по предельно допустимому числу Маха 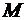 , по предельно допустимому скоростному напору
, по предельно допустимому скоростному напору  .
.
В качестве критерия оптимальности выберем теперь время перемещения самолета из начальной точки А в конечную В. Локальные затраты времени подсчитываются следующим образом:
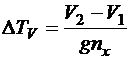 , (4.4)
, (4.4)
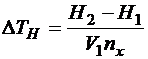 . (4.5)
. (4.5)
Результаты пересчета изолиний тангенциальной перегрузки в 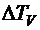 ,
, 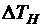 показаны на рис. 4.4. Там же показан оптимальный режим полета.
показаны на рис. 4.4. Там же показан оптимальный режим полета.
Результаты оптимизации дали классическую траекторию набора высоты самолетом-перехватчиком: резкий набор высоты на дозвуковой скорости, переход через скорость звука ( 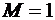 ) на некоторой постоянной высоте, затем – резкий набор высоты на сверхзвуковых скоростях с выходом на предельно допустимые числа Маха.
) на некоторой постоянной высоте, затем – резкий набор высоты на сверхзвуковых скоростях с выходом на предельно допустимые числа Маха.
4.2. Задача аналитического конструирования автопилота, управляющего продольным движением крылатой ракеты
Рассмотрим возмущенное движение крылатой ракеты, летящей на постоянной высоте. Изолированное движение по углу тангажа 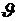 описывается следующей системой линеаризованных дифференциальных уравнений (рис. 4.5)
описывается следующей системой линеаризованных дифференциальных уравнений (рис. 4.5)
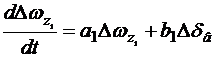 ,
,
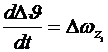 . (4.6)
. (4.6)
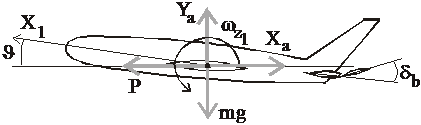
Рис. 4.5. Система сил, действующая
