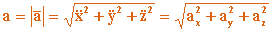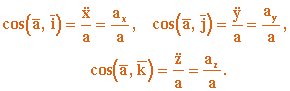Введение в кинематику. Основные задачи кинематики.

Кинематика – раздел теоретической механики, изучающий механическое движение без учета сил, вызывающих это движение, состоит из двух отделов: Кинематика точки и Кинематика твердого тела.

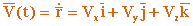Кинематика твердого тела – изучает движение твердого тела, кинематика точки используется для получения новых зависимостей и формул. Кинематика точки –изучает движение материальной точки, является базой для изучения движения точек твердого тела. Задачи кинематики состоят в разработке способов задания движения точки (системы) и методов определения скорости, ускорения точки и других кинематических величин точек, составляющих механическую систему.

50 Способы задания движения точки. Векторный способ задания движения. Скорость и ускорение.

Задание движения точки – необходимо иметь возможность определения положения точки в пространстве в любой момент времени (уравнения, геометрия механизма и известный закон движения ведущего звена).

Траектория движения точки – совокупность положений точки в пространстве при ее движении.

Три способа задания движения точки: 1.векторный, 2.координатный, 3.естественный.

Векторный способ:Сравним два положения точки в моменты времени t и t₁= t + Dt:

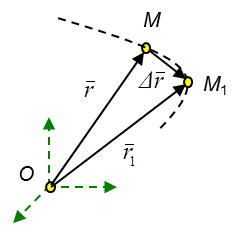
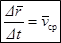
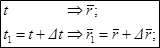- это вектор средней скорости в интервале времени Dt,

направлен по направлению вектора перемещения (хорде MM₁).

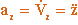
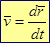Устремим Dt ® 0 и перейдем к пределу: 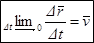. Предел отношения приращения функциик приращению приращения аргументаестьпроизводная функции (по определению): .

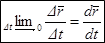- это вектор истинной скорости точки в момент времени t, направлен по касательной к траектории

(при приближении M₁к M хорда занимает положение касательной). Сравним скорости точки в двух положениях точки в моменты времени t и t₁= t + Dt: 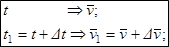. 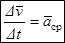- это вектор среднего ускорения в интервале времени Dt, направлен в сторону вогнутости траектории. Переходя к пределу получаем:

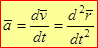- это вектор истинного ускорения точки в момент времени t, лежит в соприкасающейся плоскости (предельное положение плоскости, проведенной через касательную в точке M и прямую, параллельную касательной в точке M₁, при стремлении M₁к M) и направлен в сторону вогнутости траектории.

51 Координатный способ задания движения точки. Скорость и ускорение.

Пусть Охуz – неподвижная декартовая система координат, 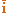, , 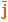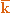- орты ее осей. Тогда вектор-функция 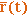может быть задана тремя скалярными функциями 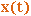, , 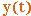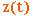– координатами точки M :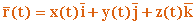
1. Чтобы знать закон движения точки, надо знать значения координат точки для каждого момента, т. е. знать зависимости

, ,

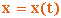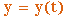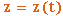(2.3)

Тогда уравнения (2.3) представляют собой уравнения движения точки в декартовых прямоугольных координатах.

2. Если движение точки совершается все время в одной и той же плоскости, то приняв эту плоскость за плоскость Oxy , получим в этом случае два уравнения движения:

,

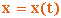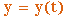(2.4)

Уравнения (2.3) или (2.4) представляют собою одновременно уравнения траектории точки в параллельном виде. Исключив из уравнений время t , можно получить уравнение траектории в явном виде (координатной форме).
Для скорости имеем выражение: , где 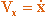, , 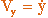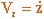- проекции скорости на оси Ox , Oy , Oz . Модуль скорости и ее направления определяются равенствами:

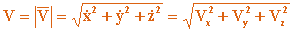(2.5)

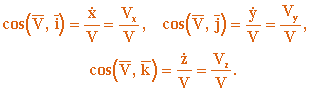
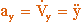Аналогично для ускорения 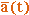получаем: 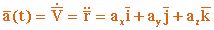, где 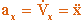, , - проекции 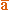на оси Ox, Oy, Oz. И тогда: