Активные силы и реакции связей.

Основные понятия статики.

Статика - раздел механики о силах и условиях равновесия материальных тел, находящихся под действием сил. Равновесие - состояния покоя тела по отношению к другим материальным телам.

Основные понятия:

Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется силой. Сила является величиной векторной. Ее действие на тело определяется: 1) численной величиной или модулем силы, 2) направлением силы, 3) точкой приложения силы, (рис. 1).

Совокупность сил, действующих на какое-нибудь твердое тело, называется системой сил. Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным. Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными. Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или эквивалентной нулю. Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил. Внешними называются силы, действующие на частицы данного тела со стороны других материальных тел. Внутренними называются силы, с которыми частицы данного тела действуют друг на друга. Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной. Силы, действующие на все точки данного объема или данной части поверхности тела, называются распределенными.

2. Аксиомы статики.

Аксиома инерции – Под действием взаимно уравновешенной системы сил тело находится в состоянии покоя или равномерного прямолинейного движения.

Аксиома двух сил – Если тело под действием двух сил находится в равновесии, то эти силы равны по модулю и направлены по одной прямой в противоположные стороны. Такие две силы представляют собой простейшую взаимно уравновешенную систему сил.

3. Аксиома присоединения – Если к заданной системе сил присоединить (или изъять) взаимно уравновешенную систему сил, то кинематическое состояние тела не изменится.

Следствие из аксиомы присоединения Кинематическое состояние тела не изменится, если силу перенести по линии ее действия

4. Аксиома параллелограмма – Равнодействующая двух пересекающихся сил равна диагонали параллелограмма, построенного на этих силах как на сторонах

5. Аксиома действия и противодействия – Всякому действию соответствует равное и противоположное противодействие (III закон Ньютона).

6. Аксиома отвердевания– Равновесие деформируемого тела сохраняется при его затвердевании (обратное справедливо не всегда).

Защемление

Любые перемещения точки крепле­ния невозможны.
Реактивную силу принято предста­влять в виде двух составляющих вдоль осей координат. R = R_x + R_y.

1. 4. Основные задачи статики.

Содержание статики абсолютно твердого тела составляют две основные задачи:

1. Задача о приведении системы сил: как данную систему сил заменить другой, наиболее простой, ей эквивалент­ной? 2. Задача о равновесии: каким условиям должна удовлетворять система сил, приложенная к данному телу (или материальной точке), чтобы она была уравновешенной системой? Вторая задача часто ставится в тех случаях, когда равновесие заведомо имеет место, например, когда заранее известно, что тело находится в равновесии, которое обеспечивается связями, наложен­ными на тело. При этом условия равновесия устанавливают зави­симость между всеми силами, приложенными к телу. С помощью этих условий удается определить опорные реакции. Определение реакций связей (внеш­них и внутренних) необходимо для последующего расчета (4.Продолжение) прочности конструкции. В более общем случае, когда рассматривается система тел, име­ющих возможность перемещаться друг относительно друга, одной из основных задач статики является задача определения возможных положений равновесия.

Система сходящихся сил.

Система сходящихся сил –линии действия сил пересекаются в одной точке.

План исследования любой системы сил соответствует последовательному решению

трех вопросов : 1.Как упростить систему? 2.Каков простейший вид системы? 3.Каковы условия равновесия системы?

Перенесем все силы по линии их действия в точку пересечения (кинематическое состояние тела при этом не изменится – следствие из аксиомы присоединения). Сложим первые две силы F₁и F₂(аксиома параллелограмма). Количество сил уменьшилось на единицу. Повторим эту же операцию со следующей силой F₄.

Осталась всего одна сила, эквивалентная исходной системе сил.

Сложение сил построением параллелограммов можно заменить построением силового треугольника – выбирается одна из сил или изображается параллельно самой себе с началом в любой произвольной точке, все другие силы изображаются параллельными самим себе с началом, совпадающим с концом предыдущей силы.

Результатом такого сложения является вектор, направленный из начала первой силы к концу последней из сил.

Простейший вид системы – сила, приложенная в точке пересечения исходных сил. Таким образом, сходящаяся система сил приводится к одной силе – равнодействующей(силе, эквивалентной исходной системе сил), равной геометрической сумме сил системы.

Если равнодействующая системы оказывается не равной нулю, тело под действием такой системы силы будет двигаться в направлении равнодействующей (система сил не уравновешена). Для того, чтобы уравновесить систему достаточно приложить силу, равную полученной равнодействующей и направленной в противоположную сторону (аксиома о двух силах). Таким образом, условием равновесия системы сходящихся сил является обращение равнодействующей в ноль.

Это условие эквивалентно замкнутости силового треугольника определенным образом, а именно, направление всех сил при обходе по контуру не изменяется по направлению:

Пара сил.

Пара сил - это система двух равных параллельных сил, направленных в разные стороны (рис. 22).

Кратчайшее расстояние между линиями действия сил называют плечом пары h , а плоскость П, где лежит пара сил, является плоскостью пары. Пример: силы, действующие на стороны рамки с током в магнитном поле. На этом физическом явлении основана работа всех электродвигателей постоянного тока. Момент пары сил на плоскости(теорема о моменте пары сил)–не зависит от выбора центра приведения (полюса)и равен произведению модуля любой из сил пары на плечо пары, взятым со знаком + (плюс), если вращение плоскости под действием пары сил происходит против часовой стрелки, и со знаком – (минус) в противном случае.

В независимости момента пары от выбора полюса можно убедиться вычислением суммы моментов от каждой из сил относительно любого центра.

Свойства пар сил.

Первое свойство. Пару сил нельзя привести к сил. Пара сил (как и сила) является самостоятельным элементом статики.

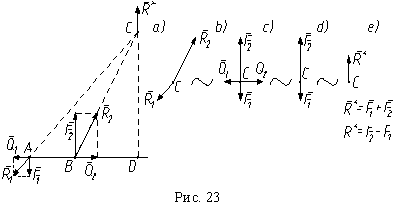Под действием пары сил свободное твердое тело может только поворачиваться. Сложим две неравные параллельные силы, направленные в разные стороны (рис. 23). Добавляем к исходной системе сил (F₁,F₂) уравновешенную систему сил (Q₁,Q₂) ~ 0. По аксиоме параллелограмма, силы, приложенные в точках A и B, эквивалентны двум непараллельным силам R₁ и R₂ (рис. 23, a). Согласно следствию второй аксиомы, переносим эти силы в точку пересечения их линий действия C (рис. 23, b). Используя вторую и третью аксиомы, раскладываем силы R₁ и R₂ на составляющие , а затем вычитаем уравновешенную систему сил (Q₁,Q₂). В результате - исходная система сил эквивалентна тем же силам, но приложенным в одной точке C, то есть (F₁,F₂) = (F₁,F₂)_C . По аксиоме параллелограмма эта система, а следовательно, и исходная система сил, эквивалентна одной силе или равнодействующей:

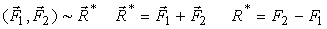(1)

Равнодействующая и ее линия действия CD параллельны исходным силам, а точка D лежит вне отрезка AB. При сложении двух параллельных сил, направленных в одну сторону, величина равнодействующей будет равна R* = F₁ + F₂, а точка D будет лежать внутри отрезка AB.

Второе свойство. Действие пары сил на твердое тело определяется моментом пары, который является свободным вектором, перпендикулярным плоскости пары, численно равным произведению силы на плечо пары.

(продолжение19)Выбираем в пространстве произвольный центр O (рис. 24) и вычисляем относительно этого центра сумму моментов сил, образующих пару. Эта сумму - моментом пары. Положение точек приложения сил пары относительно центра O определяется радиус-векторами r₁, r₂ и, учитывая, что F' = -F, получим :

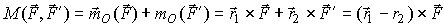Строим вектор BA, который определяет положение точки A относительно B, и на рис. 24 видим, что r₁ = r + BA или r₁ - r = BA. Учитывая это, из выражения (2) получаем:

(3)

Таким образом, действие пары сил на тело определяется ее моментом, который является мерой действия пары сил на твердое тело. Момент пары не зависит от выбора центра, то есть является свободным вектором. Величину момента пары найдем, определяя модуль векторного произведения в (3), учитывая (рис. 24), что BA sin(BA ^ F) = h:

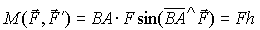
Приняв за центр O последовательно точки приложения сил A и B, по формуле (2) имеем :

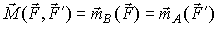
Следствия из второго свойства пары. 1. Действие пары на твердое тело не изменяется, если пару сил поворачивают в плоскости пары. 2. Действие пары сил на твердое тело не изменяется, если пару сил переносят в другое место плоскости пары. 3. Действие пары сил на твердое тело не изменяется, если ее перенести в плоскость, параллельную плоскости пары. В плоской системе сил, когда все силы и пары сил лежат в одной плоскости, моменты пар направлены перпендикулярно этой плоскости и поэтому параллельны друг другу, в этом случае, момент пары рассматривают как алгебраическую величину, равную

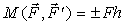(6)

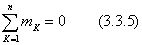20. Сложение пар сил в пространстве и плоскости.Подобно силам, пары можно складывать. Пара, заменяющая собой действие данных пар, называется результирующей. Теорема: Система пар, лежащих в одной плоскости, эквивалентна одной паре, лежащей в той же плоскости и имеющей момент,равный алгебраической сумме моментов слагаемых пар. Пусть на тело действуют три пары сил с моментами 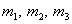. Используя теорему об эквивалентности пар, заменяем эти пары эквивалентными другими парами ,имеющими общее плечо d и такие же моменты 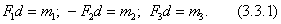Сложив отдельно силы получим: 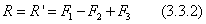Вся система заменится одной парой с моментом 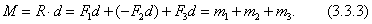Обобщая эту формулу , получим: Для равновесия плоской системы пар необходимо и достаточно, чтобы алгебраическая сумма моментов этих пар была равна нулю:

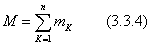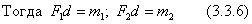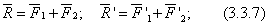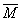При сложении пар в пространстве достаточно будет рассмотреть две пары. Теорема: Любая система пар, действующая на твердое тело, эквивалентна одной паре с моментом, равным геометрической сумме моментов слагаемых пар. Итак, пусть даны две пары с моментами m1 и m2, лежащие в плоскостях I и II . Складываем силы в точках А и В: и убеждаемся, что пары заменяются одной парой . Найдем момент этой пары:

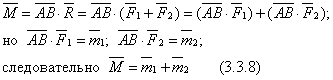Если на тело действует л пар с моментами , то:

Геометрически вектор 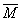- это замыкающий вектор силового многоугольника. Если векторы лежат в разных плоскостях, то можно ввести систему координат Oxyz и находить 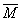аналитически:

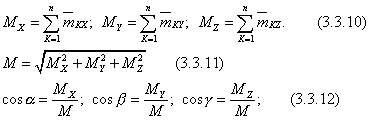
Условия равновесия пар.

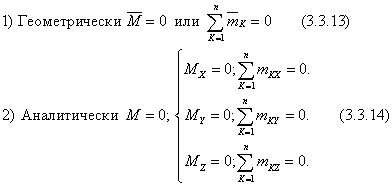Условия равновесия пространственной системы пар, запишутся:

Если в результате сложения пар 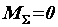, то действующие на тело пары образуют уравновешенную систему. Следовательно, необходимое и достаточное условие равновесия системы пар выражается одним уравнением
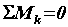,т. е. для равновесия системы пар сил, действующих на тело в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма их моментов была равна нулю. Значит, систему пар или одну пару можно уравновесить только парой.

22. Приведение силы к заданному центру.

Теорема о параллельном переносе силы: силу F, не изменяя ее действие на абсолютно твердое тело, можно переносить из данной точки (А) в любую другую точку (О) тела, прибавляя при этом пару с моментом (m), равным моменту переносимой силы относительно точки (О), куда сила переносится [m = m_o (F)]; F F, m. Приведение системы сил F₁, F₂, ..., F_n к произвольном центру (точке) О, т. е. замене данной системы сил другой эквивалентной более простой, происходит с помощью Теоремы Пуансо: любая система сил F₁, F₂, ..., F_n действующих на абсолютно твердое тело, при приведении к произвольному центру О заменяется одной силой R, равной главному вектору системы сил, приложенной в центре О и парой сил с моментом M_o, равным главному моменту системы сил относительно центра (точки) О. Главный вектор:

R = F1 + F2 + ... + Fn = ∑Fk, (k = 1, 2, ..., n)

а главный момент системы сил относительно центра (точки) О:

Mo = m1 + m2 + ... + mn = mo(F1) + mo(F2) + ... + mo(Fn) = mo(Fk). (k = 1, 2, ..., n)

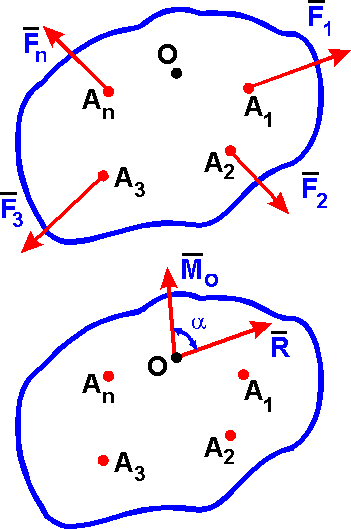Величина главного вектора R не зависит от выбора центра О, а значение главного момента M_o при изменении положения центра О может в общем случае изменяться. Для плоской системы сил F₁, F₂, ..., F_n главный вектор R лежит в плоскости действия сил, а главный момент перпендикулярен этой плоскости ( = 90). Поэтому главный момент плоской системы сил относительно центра О определяется как сумма алгебраических моментов сил относительно точки (центра) О: M_o = m_o(F_k), (k = 1, 2, ..., n) и изображается на плоскости дуговой стрелкой.

Равновесие системы сил.

Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом. Если система уравновешена, то получаем условия равновесия: R=0, M_o=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных: ∑x_i =0, ∑M_ix=0; ∑y_{i =0}, ∑M_iy=0; ∑z_i =0, ∑M_iz=0.

Для плоской системы сил (например, в плоскости Oxy ) из этих уравнений получаются только три: ∑x_i=0; ∑y_i=0; ∑M_o=0,

причем оси и точка O , относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия: ∑x_i =0; ∑M_A=0; ∑M_B=0.

Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B :

∑M_A=0; ∑M_B=0; ∑M_C=0.

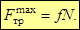Это третья форма уравнений равновесия, причем точки A , B и C не должны лежать на одной прямой. При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а): ∑x_i =0; ∑M_o=0.

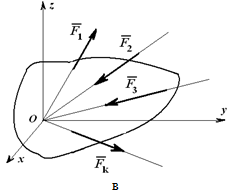
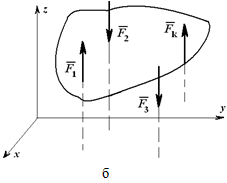
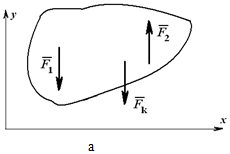
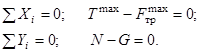Рисунок 1.26

Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия: ∑z_i =0; ∑M_ix=0; ∑M_iy=0.

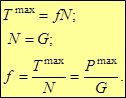Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы: ∑x_i =0; ∑y_{i =0}; ∑z_i =0

и два уравнения для плоской системы: ∑x_i =0; ∑y_{i =0}.

В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.

Трение покоя.

Трение – один из видов взаимодействия тел. Оно возникает при соприкосновении двух тел. Трение подчиняется третьему закону Ньютона: если на одно из тел действует сила трения, то такая же по модулю, но направленная в противоположную сторону сила действует и на второе тело. Силы трения возникают вследствие взаимодействия между атомами и молекулами соприкасающихся тел. Сила сухого трения - сила, возникающая при соприкосновении двух твердых тел при отсутствии между ними жидкой или газообразной прослойки. Сухое трение, возникающее при относительном покое тел, называют трением покоя. Сила трения покоя всегда равна по величине внешней силе и направлена в противоположную сторону (рис. 1.13.1).

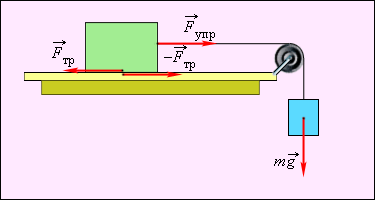
Рисунок 1.13.1.

Сила трения покоя (υ = 0).

Сила трения покоя не может превышать некоторого максимального значения (F_тр)_max. Если внешняя сила больше (F_тр)_max, возникает относительное проскальзывание.

Трение скольжения.

Если внешняя сила больше (F_тр)_max, возникает относительное проскальзывание. Силу трения в этом случае называют силой трения скольжения. Она всегда направлена в сторону, противоположную направлению движения и зависит от относительной скорости тел. Во многих случаях приближенно силу трения скольжения можно считать независящей от величины относительной скорости тел и равной максимальной силе трения покоя (рис. 1.13.2).

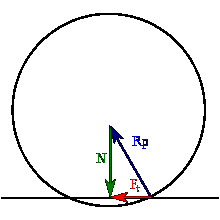
Сила трения скольжения пропорциональна силе нормального давления тела на опору, а следовательно, и силе реакции опоры. F_тр = (F_тр)_max = μN Коэффициент пропорциональности μ называют коэффициентом трения скольжения. Коэффициент трения μ – величина безразмерная. Обычно коэффициент трения меньше единицы. При скольжении сила трения направлена по касательной к соприкасающимся поверхностям в сторону, противоположную относительной скорости (рис. 1.13.3).

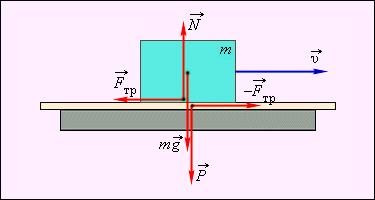
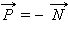На рисунке: – сила реакции опоры, – вес тела.

Законы трения.

Основные законы трения (Амонтона - Кулона):

1. Сила трения лежит в касательной плоскости к соприкасающимся поверхностям и направлена в сторону противоположную направлению, в котором приложенные к телу силы стремятся его сдвинуть или сдвигают в действительности (реактивный характер). .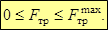

2. Сила трения изменяется от нуля до своего максимального значения. Максимальная сила трения пропорциональна коэффициенту трения и силе нормального давления .

3. Коэффициент трения есть величина постоянная для данного вида и состояния соприкасающихся поверхностей (f = const).

4. Сила трения в широких пределах не зависит от площади соприкасающихся поверхностей Способы определения коэффициента трения: 1.Сдвигающая сила изменяется от нуля до своего максимального значения – 0 ≤ T ≤ T^max, (0 ≤ P ≤ P^max). 2. Сила нормального давления изменяется от некоторого начального значения до минимального значения – N₀≥ N ≥ N^min(G₀≥ G ≥ G^min).

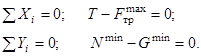
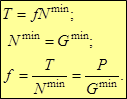
3. Сдвигающая сила и сила нормального давления изменяются при изменении угла наклона плоскости скольжения от нуля до максимального

значения – 0 ≥ φ ≥ φ^max.

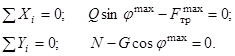
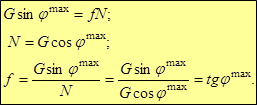
Угол и конус трения.

Угол трения.

С учетом силы трения, возникающей при контакте с шероховатой поверхностью полная реакция такой поверхности может рассматриваться как геометрическая сумма нормальной реакции абсолютно гладкой поверхности и силы трения:

Угол отклонения полной реакции шероховатой поверхности – угол трения, равный:

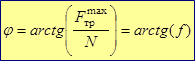При изменении направления сдвигающей силы T на опорной поверхности ее поворотом относительно нормали к плоскости полная максимальная реакция шероховатой поверхности описывает конус трения.

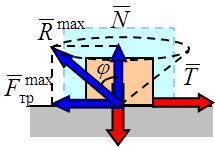
Активные силы (G, T и др.) можно заменить равнодействующей силой P, имеющей угол отклонения от вертикали α. Можно показать, что равновесие возможно лишь в том случае, когда эта сила остается внутри пространства конуса трения: Условие равновесия по оси x: Psinα ≤ F_тр^max. Из уравнения равновесия по оси у: N = Pcosα. Максимальная сила трения F_тр^max= fN = tgφN = tgφPcosα. Тогда Psinα ≤ tgφPcosα, откуда tgα ≤ tgφ и α ≤ φ.

41 Трение качения.

Трение верчения.

Также существует трение верчения – когда активные силы стремятся вращать тело вокруг нормали к общей касательной поверхности соприкосновения.

Рассмотрим шар на горизонтальной поверхности. Если к нему приложить пару с моментом , направленным по нормали к поверхности, то пара будет стремиться повернуть шар вокруг нормали. Шар начнет вращаться в том случае если приложенный момент будет больше некоторой предельной величины: , где N - нормальное давление шара на плоскость, а - коэффициент трения верчения, имеющий размерность длины. Этот коэффициент в раз меньше коэффициента трения качения и зачастую в подпятники вставляют шарик.

Плоские фермы.

Плоские фермы –Геометрически неизменяемые стержневые конструкции, стержни которых лежат в одной плоскости.

Узлы фермы – точки, в которых сходятся оси стержней (опорные узлы – узлы, которыми ферма опирается на основание).

Верхний и нижний пояса – стержни, образующие верхний и нижний контуры.. Стойки – вертикальные стержни.

Раскосы – наклонные стержни.

Пролет фермы – расстояние между опорными узлами (l).

Длина панели – расстояние между стойками (d).

Методы расчета. Для расчета усилий, возникающих в стержнях ферм, используются метод вырезания узлов и метод сквозных сечений (метод Риттера).

Основные допущения, принимаемые при расчете ферм:

1. Все узлы соединения стержней считаются идеальными шарнирами, не препятствующими взаимному повороту стержней. Узлы в металлических фермах, в которых стержни соединяются при помощи фасонных листов и заклепок, также рассматриваются как шарнирные, поскольку при нагрузке они допускают малые упругие деформации (взаимные повороты).

2. Нагрузка приложена в узлах. Для узловой передачи нагрузки на практике используются специальные балочные конструкции.

3.Геометрические размеры фермы не изменяются при нагружении (деформации малы). Фермы бывают плоскими (все стержни лежат в одной плоскости) и пространственными. Плоские фермы воспринимают нагрузку, приложенную только в их плоскости, и нуждаются в закреплении их связями. Пространственные фермы образуют жесткий пространственный брус, воспринимающий нагрузку в любом направлении.

44 Расчет плоских ферм ( способ вырезания узлов).

Метод вырезания узлов: последовательно вырезаются узлы фермы так, чтобы в двух уравнениях равновесия для каждого из узлов было не более двух неизвестных усилий. Как правило, внешние опорные реакции должны быть предварительно определены.

Порядок расчета:

1. Выбираем в качестве объекта равновесия ферму в целом и определяем опорные реакции:

2. Нумеруем или обозначаем буквами необозначенные узлы. Реакции стержней (или усилия в них) будем обозначать далее двумя индексными цифрами или буквами – первая из них совпадает с номером (обозначением) вырезаемого узла, а вторая указывает- к каком узлу присоединяется другим концом рассматриваемый стержень.

3. Вырезаем узел A (в этом узле всего два неизвестных усилия) и заменяем действие разрезанных

(отброшенных) узлов усилиями (реакциями) S_A1и S_A6.

4.Составляем уравнения равновесия для узла A и вычисляем усилия S_A1и S_A6.

5. Вырезаем узел 1 (в этом узле всего два неизвестных усилия) и заменяем действие разрезанных

(отброшенных) узлов усилиями (реакциями) S_1A, S₁₂ и S₁₆.

6. Составляем уравнения равновесия для узла 1 и вычисляем усилия S₁₂и S₁₆ (S_1Aи S_A1равны алгебраически, поскольку при направлении неизвестных усилий от узла аксиома действия и противодействия выполняется автоматически) .

Далее процесс вырезания узлов и определения усилий повторяется в определенном порядке, например:

2, 6, 7, 3, 4, 8, 5.

Метод вырезания узловдля вычисления усилия только в указанном стержне требует рассмотрения всех узлов и решения для них уравнений равновесия (по крайней мере узлов, находящихся между одним из опорных узлов и узлом, к которому подходит указанный стержень).

45 Расчет плоских ферм ( способ Риттера).

Метод сквозных сечений (метод Риттера)в большинстве случаев нетребует для вычисления усилия только в указанном стержне составления каких-либо других вспомогательных уравнений равновесия кроме того уравнения, в котором непосредственно участвует искомое усилие.

Метод основывается на составлении одного уравнения равновесия с использованием II и III форм уравнений равновесия произвольной плоской системы сил.

Порядок расчета:

1. Выбираем в качестве объекта равновесия ферму в целом и определяем опорные реакции:

2. Проводим сквозное сечение, разделяющее ферму на две отдельные части так,

чтобы в сечение попадало не более трех стержней, в одном из которых требуется

найти усилие, например, сечение I-I для определения S₂₃.

3. Выбирая в качестве объекта равновесия одну часть, например, правую, отбрасываем

другую (левую) часть.

4. Действие отброшенной части на оставшуюся заменяем реакциями стержней, попавших в разрез – S₃₂, S₃₆и S₇₆.

5. Для искомого усилия S₃₂ находим положение точки Риттера, как точки пересечения линий действия двух других усилий S₃₆и S₇₆, не подлежащих определению в данный момент. Точка Риттера для усилия S₃₂совпадает с узлом 6.

(45 продолжение)6. Составляем моментное уравнение равновесия для оставленной (правой) части относительно найденной точки Риттера (узла 6) и определяем искомое усилие.

7. Для определения усилия S₇₆ находим положение точки Риттера, как точки пересечения линий действия двух других усилий S₃₆и S₃₂, не подлежащих определению в данный момент. Точка Риттера для усилия S₇₆совпадает с узлом 3.

8. Составляем моментное уравнение равновесия для оставленной (правой) части относительно найденной точки Риттера (узла 3) и определяем искомое усилие.

7. При определении усилия S₃₆ точка Риттера, как точка пересечения линий действия двух других усилий S₇₆и S₃₂, не подлежащих определению в данный момент, уходит в бесконечность. В этом случае моментное уравнение равновесия вырождается в уравнение равновесия в проекциях на ось, перпендикулярную линиям, уходящим в бесконечность.

Для определения других усилий необходимо провести другое сечение (п.2) и повторить описанные действия.

Основные понятия статики.

Статика - раздел механики о силах и условиях равновесия материальных тел, находящихся под действием сил. Равновесие - состояния покоя тела по отношению к другим материальным телам.

Основные понятия:

Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется силой. Сила является величиной векторной. Ее действие на тело определяется: 1) численной величиной или модулем силы, 2) направлением силы, 3) точкой приложения силы, (рис. 1).

Совокупность сил, действующих на какое-нибудь твердое тело, называется системой сил. Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным. Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными. Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или эквивалентной нулю. Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил. Внешними называются силы, действующие на частицы данного тела со стороны других материальных тел. Внутренними называются силы, с которыми частицы данного тела действуют друг на друга. Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной. Силы, действующие на все точки данного объема или данной части поверхности тела, называются распределенными.

2. Аксиомы статики.

Аксиома инерции – Под действием взаимно уравновешенной системы сил тело находится в состоянии покоя или равномерного прямолинейного движения.

Аксиома двух сил – Если тело под действием двух сил находится в равновесии, то эти силы равны по модулю и направлены по одной прямой в противоположные стороны. Такие две силы представляют собой простейшую взаимно уравновешенную систему сил.

3. Аксиома присоединения – Если к заданной системе сил присоединить (или изъять) взаимно уравновешенную систему сил, то кинематическое состояние тела не изменится.

Следствие из аксиомы присоединения Кинематическое состояние тела не изменится, если силу перенести по линии ее действия

4. Аксиома параллелограмма – Равнодействующая двух пересекающихся сил равна диагонали параллелограмма, построенного на этих силах как на сторонах

5. Аксиома действия и противодействия – Всякому действию соответствует равное и противоположное противодействие (III закон Ньютона).

6. Аксиома отвердевания– Равновесие деформируемого тела сохраняется при его затвердевании (обратное справедливо не всегда).

Активные силы и реакции связей.