Интервальные оценки. Доверительный интервал для оценки математического ожидания. Распределение Стьюдента.

Интервальной назыв оценку, кот определяется двумя числами — концами интервала, кот с определенной вер-тью накрывает неизвестный параметр генер-ной сов-ти. Интервал, содержащий оцениваемый параметр генеральной совокупности, называют доверительным интервалом. Для его определения вычисляется предельная ошибка выборки 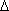, позволяющая установить предельные границы, в которых с заданной вероятностью (надежностью) д находиться параметр генер-ой сов-ти. Предельная ошибка выборки равна t-кратному числу средних ошибок выборки. Коэффициент t позволяет установить, насколько надежно высказывание о том, что заданный интервал содержит параметр генеральной совокупности. Если выбирается коэффициент таким, что высказывание в 95% случаев окажется правильным и только в 5% — неправильным, то говорится, что: со статистической надежностью в 95% доверительный интервал выборочной статистики содержит параметр генеральной совокупности. Для оценки математического ожидания нормально распределенного количественного признака X по выборочной средней при неизвестном среднем квадратическом отклонениигенеральной совокупности (на практике — при малом объеме выборки, т. е. при n < 30) и собственно-случайном повторном отборе формула имеет вид 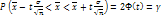, где t определяется по таблицам Лапласа, из соотношения 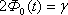; — среднее квадратическое отклонение; n — объем выборки.

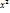Распределение Стьюдента получило свое название от псевдонима Student, которым английский ученый Госсет подписывал свои работы по статистике. Пусть Z – нормальная случайная величина, причем M(Z)=0, (Z)=1, а V – независимая от Z величина, кот распределена по закону с k степенями свободы. Тогда величина 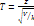имеет распределение, кот назыв t-распределением или распределением Стьюдента с k степенями свободы. Итак, отношение нормированной нормальной величины к квадратному корню из независимой случайной величины, распределенной по закону «хи квадрат» с k степенями свободы, деленной на k, распределено по закону Стьюдента с k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному.

Статистическая, корреляционная и функциональная зависимости. Уравнения регрессии. Примеры.

Две случайные величины м.б. связаны либо функциональной зависимостью, либо зависимостью другого рода, назыв статической, либо быть независимыми. Строгая функц-ая завис-ть реализуется редко, т.к. обе величины или одна из них подвержены еще действию случайных факторов, причем среди них м.б. и общие д/обеих величин. В этом случае возникает статическая завис-ть. Например, если Y зависит от случайных факторов 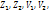а X зависит от случайных факторов 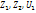, то между Y и X имеется статическая завис-ть, т.к. среди случайных факторов есть общие, а именно 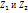. Статической назыв завис-ть, при кот изменение одной из величин влечет изменение распределения другой. В частности статическая завис-ть проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае стат-ую завис-ть назыв корреляционной. Пример: Пусть Y – урожай зерна, X – кол-во удобрений. С одинаковых по площади участков земли при равных кол-вах внесенных удобрений снимают различный урожай, т.е Y не явл ф-ей от X. Это объясняется влиянием случайных факторов (осадки, влажность, температура воздуха и т.д.). Вместе с тем, как показывает опыт, средний урожай явл ф-ей от кол-ва удобрений, т.е. Y связан с X корреляционной завис-тью.

Уравнения регрессии Yна X и X на Y: М(Y|х)=f(x), М(X|y)= (y). Условное мат-ое ожидание М(Y|х) явл ф-ей от х, следовательно, его оценка, т.е. условное среднее 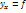*(х). Это уравнение назыв выборочным уравнением регрессии Y на X; ф-ию 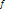*(х) назыв выборочной регрессией Y на X, а ее график – выборочной линией регрессии Y на X. Аналогично уравнение 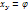*(y) назыв выборочным уравнением регрессии X на Y; ф-ию *(х) назыв выборочной регрессией X на Y, а ее график – выборочной линией регрессии X на Y.

Коэффициент корреляции и его свойства. Нахождение уравнений регрессии по корреляционной таблице. Примеры.

Коэффициент корреляции — показатель характера изменения двух случайных величин. R.

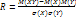. Св-ва: 1) если Х и У нсв, то 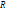=0; 2) -1 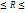1. При этом, если |r| =1, то м/у Х и У функциональная , а именно линейная зав-ть; 3) 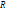характеризует относительную величину отклонения М(ХУ) от М(Х)М(У), и т.к. отклонение имеет место только для зависимых величин, то 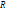характеризует тесноту зависимости.

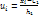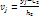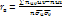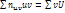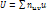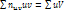Пусть требуется по данным корреляционной таблицы вычислить выборочный коэффициент корреляции. М значительно упростить расчет, если перейти к условным вариантом и . В этом случае выборочный коэффициент корреляции вычисляют по формуле: . М доказать, что справедливы формулы: , где ; , где 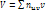. Д/контроля целесообразно выполнить расчеты по обеим формулам и сравнить рез-ты; их совпадение свидетельствует о правильности вычислений.

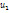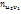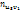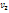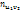Найдем 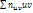2-мя способами: суммируя произведения частот 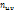на произведения соответствующих условных вариант 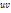по строкам и столбцам. Д/1-ой строки таблицы: 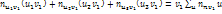. Д/2-ой строки таблицы:

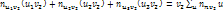. Сложим 1-ую и 2-ую строчку: 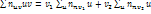. Итак, 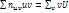, где 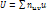. Аналогично, суммируя произведения частот 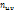на произведения соответствующих условных вариант 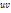по столбцам, получим: 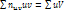, где .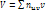

Пр: Вычислить 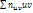по данным корреляционной таблицы

Y	Х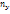
			-	-	-	-
	-			-	-	-
	-	-				-
	-	-
	-	-
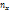							n=200

Решени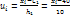е: , где 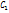– х=40 примерно середина вариационного нуля; шаг 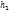равен разности м/у двумя соседними вариантами. 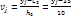. Составим корреляционную таблицу в условных вариантах:

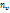-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-
	-	-
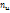							n=200

В каждой клетке, в кот частота 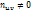, записывают в правом верхнем углу произведение частоты 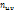на варианту u, например, 5*(-3)=-15 и т.д. Складывают все числа, помещенные в правых углах одной строки и их сумму записывают в клетку той же строки столбца 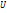. Умножают варианту на 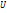и полученное произведение записывают в последнюю клетку той же строки, т.е. в клетку столбца 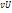. Наконец, сложив все числа этого столбца, получают сумму 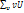, кот равна искомой сумме 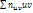, например, 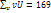, то и 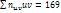. Для контроля аналогичные вычисления производят по столбцам .

Статическая проверка статических гипотез. Основная и альтернативная гипотезы. Ошибки первого и второго рода. Уровень значимости. Мощность критерия. Экспериментальные и критические значения. Критические области.

Статической назыв гипотеза о виде неизвестного распределения, или о параметрах известных распределений. Например, генеральная сов-ть распределена по закону Пуассона. Нулевой, или основной назыв выдвинутую гипотезу 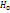. Конкурирующей, или альтернативной назыв гипотезу 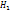, кот противоречит нулевой. Например, если нулевая гипотеза состоит в предположении, что мат-ое ожидание а нормального распределения равно 10, то конкурирующая гипотеза м состоять в предположении, что а не равно 10, т.е. 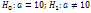. Выдвинутая гипотеза м.б. правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят стат-ими методами, ее назыв статической. В итоге стат-ой проверки гипотезы в двух случаях м.б. принято неправильное решение, т.е. м.б. допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Последствия этих ошибок м.б. весьма различны. Например, если отвергнуто правильное решение «продолжать строительство жилого дома», то эта ошибка первого рода повлечет материальный ущерб; а если же принято неправильное решение «продолжать строительство», несмотря на опасность обвала стройки, то эта ошибка второго рода м повлечь гибель людей. Критическая область – сов-ть значений критерия, при кот нулевую гипотезу отвергают. Мощность критерия – вер-ть попадания в критическую область при условии, что справедлива конкурирующая гипотеза. Т.е. мощность критерия есть вер-ть того, что нулевая гипотеза отвергнута, если верна конкурирующая гипотеза.

Гипотеза о значении генеральной средней. Связь этой гипотезы с доверительным интервалом для математического ожидания. Примеры.

Две гипотезы о равенстве математических ожиданий двух выборок. Примеры.

Гипотеза о равенстве дисперсий двух выборок. Гипотеза о существенности корреляционной связи. Примеры.

Гипотеза о виде распределения. Критерий Пирсона. Примеры.