Понятие о методе Монте-Карло.

Принято считать, что метод Монте-Карло возник в 1949 году, когда в связи с работой по созданию атомных реакторов. Нейман и Улам предложили испытать аппарат теории вер-ти д/решения прикладных задач с помощью ЭВМ. Название метода связывают с горным домом, рулеткой. Если в расчете по методу М-К моделируются величины, определяемые реальным содержанием, то расчет представляет собой прямое моделирование имитацию этого явления. Разработано моделирование на ЭВМ процесса переноса, рассеивания и размножения частиц: электронов, нейтронов, гамма-квантов. Моделирование эволюции ансамблей молекул д/решения важнейших задач квантовой стат-ой физики, моделирование массового обслуживания и производственных процессов в моделирование случайных процессов в химии, биологии, геологии и т.д.

Требуется найти значение а некоторой случайной величины. Д/этого выбирают такую случайную величину х, мат-ое ожидание кот равно а: М(х)=а. Отыскание возможных случайной величины х (моделирование) назыв «разыгрыванием» случайной величины. Теория метода М-К указывает, как наиболее целесообразно выбрать случайную величину х, как найти ее возможное значение, в частности, используемых случайных величин, в результате чего уместна ошибка, допускаемая при замене искомого мат-го ожидания, а его оценкой а. При разыгрывании случайной величины испытывают известные методы теории вер-ти.

Пример: события А и В независимы и совместимы. Разыграть 6 испытаний, в каждом из кот Р(А)=0,6 и Р(В)=0,2. Решение: т.к. А и В независимые испытания, то возможны 4 исхода испытания

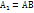Р( )= Р(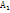А)*Р(В)=0,6*0,2=0,12

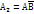Р( 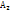)= 0,6*0,8=0,48

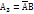Р( )= 0,4*0,2=0,08

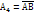Р( 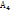)= 0,4*0,8=0,32

Т.о., задача сведена к разыгрыванию 4 событий, кот в свою очередь сводятся к разыгрыванию случайной величины х, имеющая следующий закон распределения:

х
Р(х)	0,12	0,48	0,08	0,32

Выберем 6 случайных чисел из интервала (0;1) – 0,45; 0,65; 0,06; 0,59; 0,33; 0,70. Построим частичные интервалы (0; ), ( ),…,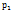

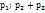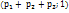
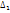= (0;0,12)

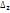= (0,12;0,60)

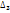= (0,60;0,68)

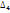= (0,68;1)

Случайное число 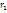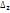, поэтому наступило событие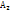 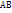, , 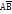, 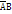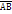. Получим искомую пос-ть исхода разыгранных событий.

Математическая статистика. Генеральная и выборочная совокупности. Репрезентативность выборки. Вариационные ряды. Полигон и гистограмма. Примеры.

МС – наука, занимающаяся методом обработки опытных данных, получаемых в результате наблюдений над случайными величинами. Задачи МС: 1.описание явления, 2.анализ и прогноз, 3.выработка оптимальных решений.

Пусть требуется изучить мн-во однородных объектов (статистическая сов-ть) относительно некоторого качеств-го или количеств-го признака, характерного д/этого объекта. Пр: имеется партия деталей, качеств-ый признак: стандартность деталей, колич-ый признак: размер детали. Идеальным вариантом явл сплошное обследование, но в большинстве случаев это сделать невозможно. В этом случае из всего мн-ва объекта выбирают часть его. Генеральная сов-ть – статист-ая сов-ть, из кот отбирают часть объектов. Выборочная сов-ть – мн-во объектов, случайно отобранных из генеральной сов-ти. Число объектов генер-ой сов-ти и выборки – их объем. Выборка д.б. репрезентативной. Считается, что выборка репрезентативна, если все объекты генер-ой сов-ти имеют одинаковую вер-ть попасть в выборку, т.е. выбор производится случайно.

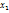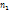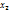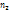Пусть из генер-ой сов-ти извлечена выборка, причем наблюдалось раз, - раз, 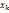- 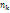раз и 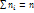- объем выборки. Наблюдаемые значения 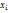- варианты, а пос-ть вариант, записанных в возрастающем порядке, - вариационные ряды. Числа наблюдений назыв частотами, а их отношение к объему выборки 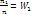- относительная частота.

Для наглядности строят различные графики стат-го распределения, в частности, полигон и гистограмму. Полигон частот – ломаная, отрезки кот соединяют точками 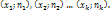Для построения полигона частот на оси абсцисс откладывают варианты 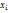, а на оси ординат соответствующие им частоты 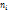. Точки ( 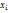; 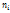) соединяют отрезками прямых и получают полигон частот. Полигон относительных частот – ломаная, отрезки кот соединяют точками 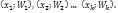Для построения полигона относительных частот на оси абсцисс откладывают варианты 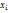, а на оси ординат соответствующие им относительные частоты 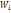. Точки ( 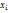; 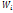) соединяют отрезками прямых и получают полигон относительных частот. В случае непрерывного признака целесообразно строить гистограмму, д/чего интервал, в кот заключены все наблюдаемые значения признака, кот разбивают на несколько частичных интервалов длиной h и находят л/каждого частичного интервала 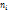- сумму частот вариант, попавших в i-тый вариант. Гистограмма частот – ступенчатая фигура, состоящая из прямоугольников, основаниями кот служат частичные интервалы h, а высоты равны отношению (плотность частоты). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии . Площадь i-того частичного прямоугольника равна 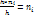- сумме частот вариант i-того интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки. Гистограмма относительных частот – ступенчатая фигура, состоящая из прямоугольников, основаниями кот служат частичные интервалы h, а высоты равны отношению 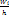(плотность относительных частоты). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии 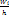. Площадь i-того частичного прямоугольника равна 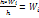- сумме относительных частот вариант i-того интервала; следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

Оценка числовых хар-к. Состоятельность, несмещенность и эффективность оценок. Оценка математического ожидания. Примеры.

Пусть требуется изучить колич-ый признак генер-ой сов-ти. Допустим, что из теоретического соображения удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, кот определяет это распределение. 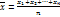. Статическая оценка неизвестного параметра теор-го распределения – ф-ия от наблюдаемых случайных величин. Для того чтобы стат-ие оценки давали «хорошие» приближения оцениваемых параметров, они д удовлетворять определенным требованиям. Пусть 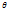* - стат-ая оценка неизвестного параметра теорит-го распределения. Допустим, что по выборке объема n найдена оценка 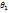*. Повторим опыт, т.е. извлечем из генер-ой сов-ти др выборку того же объема и по ее данным найдем оценку 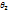*. Повторяя опыт многократно, получим числа 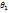*, *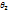…, *, 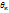кот различны м/у собой. Т.о., оценку * м рассматривать как случайную величину, а числа 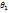*, *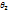…, * 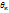- ее возможные значения. Оценка 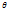* дает приближенное значение с избытком; тогда каждое найденное по данным выборок число 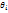*(i=1,2,…,k) больше истинного значения . Ясно, что в этом случае и мат ожидание случайной величины * больше, чем , т.е. М( *)> 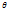. Очевидно, что если * дает оценку с недостатком, то М( *)< 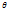. Т.о. испытание стат-ой оценки, мат ожидание кот не равно оцениваемому параметру, привело бы к стат-им ошибкам. Несмещенной назыв стат-ая оценка * мат ожидание кот равно оцениваемому параметру при любом объеме выборки. М( *)= 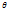. Смещенной назыв оценку, мат ожидание кот не равно оцениваемому параметру. Эффективной назыв статическая оценка, кот имеет наименьшую возможную дисперсию. Состоятельной назыв статическая оценка, кот при 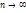стремится по вер-ти к оцениваемому параметру. Например, если дисперсия несмещенной оценки при 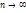стремится к нулю, то такая оценка оказывается и состоятельной.

Выборочная и исправленная дисперсии. Другие хар-ки вариации данных. Исправленная дисперсия среднего значения. Примеры.

Выборочная дисперсия 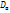- среднее арифметическое квадратов отклонения наблюдаемых значений признака от их средних значений 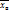. Если все значения 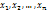признака выборки объема n различны, то 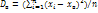. Если же значения признака 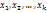имеют соответственно частоты 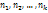, причем 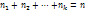, то 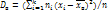, т.е. выборочная дисперсия есть средняя взвешенная квадратов отклонения с весами, равными соответствующим частотам. Выборочным средним квадратическом отклонением назыв квадратный корень из выборочной дисперсии .

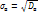Если «исправить» выборочную дисперсию так, чтобы ее мат-ое ожидание было равно генеральной дисперсии, т.е. умножить 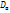на дробь 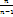, то получим исправленную дисперсию, кот обозначается через 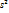. 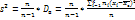= 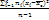. Исправленная дисперсия явл несмещенной оценкой генер-ой дисперсии. 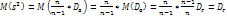. Итак, в качестве оценки генер-ой дисперсии принимают исправленную дисперсию 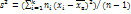. Для оценки среднего квадратического отклонения генер-ой сов-ти используют «исправленное» среднее квадратическое отклонение, кот равно квадратному корню из исправленной дисперсии .

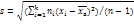Пример, выборочная совокупность задана таблицей распределения

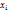1 2 3 4

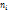20 15 10 5

Найти выборочную дисперсию.

Решение: найдем выборочную среднюю s w:val="14"/></w:rPr><m:t>50</m:t></m:r></m:den></m:f><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="14"/><w:sz-cs w:val="14"/></w:rPr><m:t>=2</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">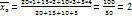

Найдем выборочную дисперсию