Закон Гука при растяжении и сжатии в относительных и абсолютных выражениях. Пределы его применимости и графическое представление. Модуль упругости материала; его физический и геометрический смысл.
Закон Гука при растяжении сжатии. Относительная продольная деформация прямо пропорциональна соответствующему нормальному напряжению,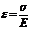
Применимость-применим только в упругих деформациях
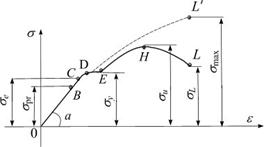
Графичское представление(з. гука и модуля упругости)
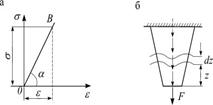
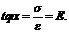
Модуль упругости материала–физ. Смысл (упругая постоянная материала, характеризующая жесткость материала при растяжении)определяется экспериментально
Растяжение и сжатие. Относительная продольная деформации. Вывод формулы для абсолютной деформации (формулы жесткости). Жесткость сечения. вычисление полного удлинения бруса и удлинение, связанное с температурным воздействием.
Растяжение и сжатие -вид нагружения бруса, при котором внутренние силы в поперечном сечении приводятся только к продольной силе N.
Продольная деформация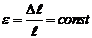 
Формула жёсткости для абсолютной деформации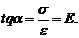 
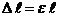и 
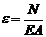.Тогда абсолютное удлинение участка стержня длиной 
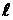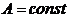при 
и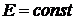 
будет равно
,
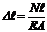EA -жесткостьстержня при растяжении ,сжатии
Вычесление полного удлинения бруса ,удлинение связанное с температурным воздействием-Если на участке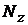 
и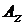 
переменны (рис. 3.9 б), то полное удлинение участка 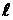получим, суммируя удлинения бесконечно малых участков dz:
.
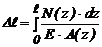Для бруса, имеющего несколько участков:
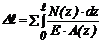. (3.14)
Удлинение, связанное с температурным воздействием:
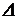
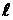to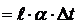 
, (3.15)
где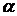 
– коэффициент температурного расширения материала; 
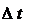– изменение температуры.
14)растяжение и сжатие. Абсолютная и относительная поперечная деформация. Связь между продольной и поперечной деформациями. Коэффициент Пуассона, его физический смысл и способы определения
Абсолютная и относительная поперечная деформация -Абсолютная поперечная деформация определяется как разность размеров после деформации и до нее:
; 
.
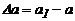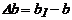Относительная поперечная деформация для изотропных материалов по всем направлениям одинакова:
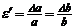
Связь между продольной и поперечной деформациями,коэфпуассона ,его физ и способы определения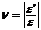 
или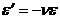 
где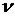 
– коэффициент поперечной деформации (коэффициент Пуассона) – безразмерная величина, упругая постоянная материала, определяемая экспериментально. Для всех изотропных материалов 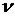= 0 ¸ 0,5. Для пробки 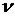»0; для каучука 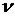» 0,5; для стали 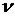» 0,3.
15.Перемещение поперечного сечения при растяжении и сжатии. Дифференцальная зависимость между перемещением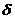 
и продольной силой N. Построение эпюры перемещений(пример). Условие жесткости.
Перемещение поперечного сечения при растяжении сжатии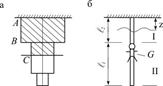 
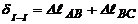(под буквой а )
Диференциальная зависимость м/у перемещением и продольной силой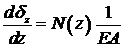 
.
Пример построения эпюры-Эпюру перемещений начинают строить от защемленного конца, вычисляя перемещения характерных сечений
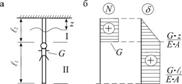
Рис. 3.11
I участок,0<z< 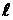1: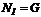 
;
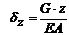(линейный закон), при 
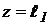перемещение 
.
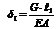II участок,0<z< 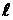2: 
, 
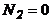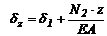;или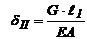 
(const).
Для обеспечения нормальной работы конструкций размеры их элементов необходимо выбирать так, чтобы выполнялось условие жесткости,которое состоит в ограничении упругих перемещений:
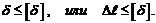(3.19)
где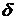 
и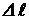 
– наибольшее перемещение; 
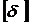–допускаемое перемещение.