Площадь сечения; статические моменты; центр тяжести для простых и сложных фигур. Центральные оси. Координаты центра тяжести.

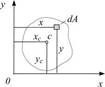
Рассмотрим произвольную фигуру (поперечное сечение бруса), связанную с координатными осями Оx и Оy.

Выделим элемент площади dA с координатами х, у. Площадь сечения равна сумме элементарных площадок

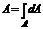. (6.1)

Статическим моментом сечения относительно данной оси называется взятая по всей его площади A cумма (интеграл) произведений элементарных площадок dA на их расстояния до этой оси.

Так статические моменты площади сечения относительно осей x и y определяются по формулам:

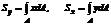. (6.2)

Статические моменты измеряются в единицах длины в кубе и выражаются в см³, м³. В зависимости от знаков координат они могут принимать положительные значения, отрицательные и равные нулю.

Пусть x_c и y_c – координаты центра тяжести фигуры (рис.6.1). На основании теоремы Вариньона (из курса теоретической механики) можно записать:

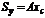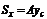, , (6.3)

где А- площадь фигуры.

Оси, проходящие через центр тяжести называется центральными. В этом случае

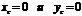, тогда 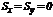. Следовательно, статические моменты относительно центральных осей равны нулю.

Если сечение можно разбить на простейшие составные части (прямоугольники, прямоугольники и т.п.), площади и положение центров тяжести которых известны, то статический момент площади всего сечения относительно любой оси (рис. 6.2) равен алгебраической сумме статических моментов составляющих фигур относительно той же оси:

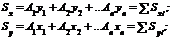(6.4)

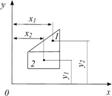
Рис.6.2

По формулам (6.3) и (6.4) легко найти координаты центра тяжести сложной фигуры:

(6.5)

, .

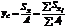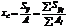Пример 6.1. Определить положение центра тяжести сечения (рис.6.3)

Решение. Сечение симметрично относительно оси у . Следовательно, центр тяжести С лежит на этой оси, т.е. координата х_с=0, и остается найти координату у_с. Все размеры показаны на рисунке в сантиметрах.

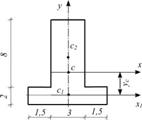
Рис.6.3

Разбиваем фигуру на два прямоугольника: первый – с центром тяжести С₁ и площадью

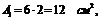
Второй – с центром тяжести С₂ и площадью

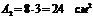
За вспомогательную ось принимаем центральную ось первого прямоугольника х₁. Тогда статический момент его площади 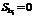. Статический момент площади второго прямоугольника согласно формулам (6.3) составляет

.

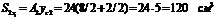Координата центра тяжести всего сечения согласно формулам (6.5):

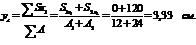
Положительное значение свидетельствует о том, что центр тяжести С лежит выше оси х₁.

Примечание. Заметим, что точка С лежит на прямой С₁С₂ соединяющей центры тяжести прямоугольников, и разбивает ее на отрезки обратно пропорциональные площадям:

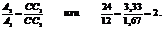
Расчет по предельным состояниям. Понятие и критерий предельного состояния конструкции (сооружения). СНиП. Две группы предельных состояний и расчеты на прочность и жесткость. Коэффициенты, учитывающие отклонения различных факторов от нормативных значений. Нормативная и расчетная нагрузка. Нормативное и расчетное сопротивление материала. Условие прочности (идея). Условие прочности при растяжении и сжатии. Пример расчета. Область применения этого метода.