Теорема о сложении ускорений точек

Ускорение любой точки тела, совершающего плоское движение, определяется как сумма ускорения полюса и ускорения данной точки во вращательном движении вокруг полюса

движение относительно неподвижной системы отсчета называетсяабсолютным

движение относительно подвижной системы отсчета называетсяотносительным

движение подвижной системы относительно неподвижной системы отсчета называетсяпереносным

Теорема о сложении скоростей

Если точка М не движется относительно подвижной системы отсчета, то, и ее абсолютная скорость совпадает тогда со скоростью движения подвижной системы отсчета относительно неподвижной

По определению это и есть скорость переносного движения

Теорема. Абсолютная скорость точки равна

сумме относительной и переносной скоростей

Теорема Кориолиса

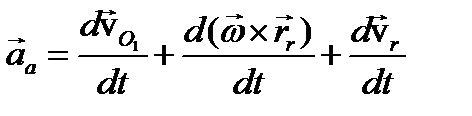
Если точка покоится относительно подвижной системы отсчета, то ее движение совпадает с переносным движением, а абсолютное ускорение – с переносным ускорением

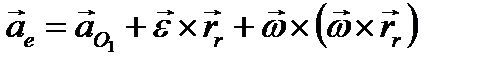
Теорема.Абсолютное ускорение точки равно сумме

относительного , переносного и кориолисова ускорений

Ускорение Кориолиса

Это ускорение обращается в нуль, если угловая скорость подвижной системы отсчета равна нулю ω=0, т. е. переносное движение поступательное

угловая скорость вращения подвижной системы отсчета параллельна

относительной скорости ω относительная скорость точки равна нулю

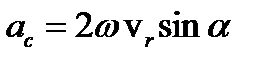Модуль ускорения Кориолиса равен

Задачи динамики

Механической системой называется совокупность взаимодействующих между собой материальных точек или тел.

Динамика изучает движение данных точек или тел, возникающее при их взаимодействии

Динамика изучает движение материальных тел под действием сил

Задачи динамики

Первая задачасостоит в определении сил, действующих на механическую систему, по заданному закону ее движения

Во второйже заданы силы, действующие на механическую систему и необходимо найти закон ее движения

На практикечасто приходится решать смешанную задачу, когда часть сил известна, а некоторые (реакции связей) необходимо найти наряду с законом движения

Закон инерции Галилея

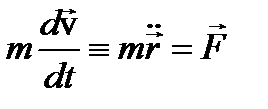Свободная материальная точка покоится или равномерно и прямолинейно двигается

Сформулированная аксиома является выражением того экспериментального факта, что отличить состояние покоя от равномерного и прямолинейного движения нельзя

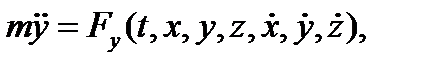Действительно, если относительно некоторой системы отсчета К точка покоится, то всегда можно построить такую систему К’, относительно которой данная точка будет двигаться равномерно и прямолинейно

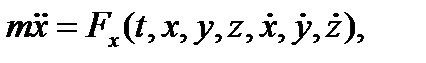
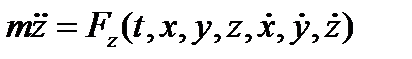
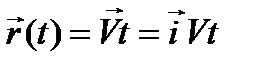
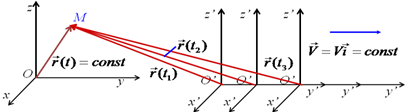Т.о., точка М в движется относительно системы К’ прямолинейно со скоростью

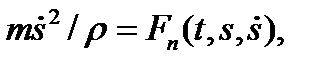Второй закон Ньютона

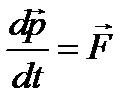
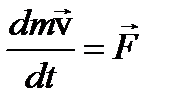аксиома 2Если в некоторой инерциальной системе отсчета на свободную материальную точку действует сила , то скорость изменения импульса (количества движения) материальной точки равна действующей на нее силе

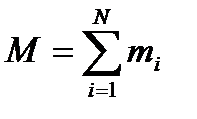Т.о., масса является мерой инерции тела. Инертность тела, т.е. его способность двигаться без изменения скорости тем больше, чем больше масса. По этой причине эту массу называют инертной

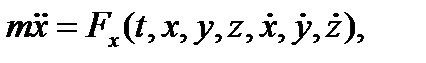Масса величина аддитивная и скалярная

В классической механике предполагается, что масса тела во всех инерциальных системах отсчета одинакова и не меняется со временем

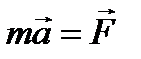
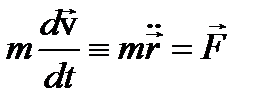
Третий закон Ньютона

Две материальные точки действуют друг на друга с

силами, равными по величине и направленными вдоль

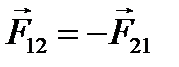
одной прямой в противоположные стороны

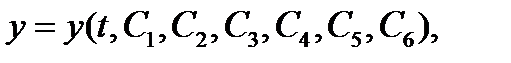
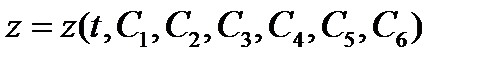
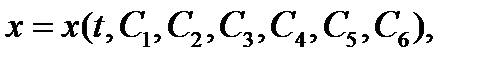
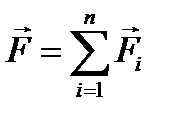
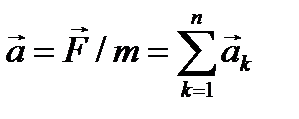Аксиома 4Действие на материальную точку произвольной системы n сил эквивалентно действию одной силы, равной их сумме

Аксиома связейВсякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их реакциями

Закон инерции Галилея постулирует существование инерциальных систем отсчета, и тем самым указывает на рамки применимости второго закона Ньютона. Сформулированные аксиомы применимы лишь в инерциальных системах отсчета