Внутренние силовые факторы. Метод сечений. Понятие о напряжениях. Связь между внутренними силовыми факторами и напряжениями.

Зависимость между моментами инерции при параллельном переносе осей и при повороте осей.

При параллельном переносе осей:

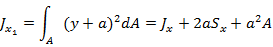
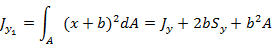
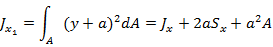
Если S_x и S_y равны нулю, тогда: ;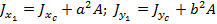

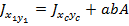
При повороте осей:

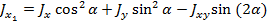
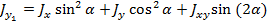
и для центробежного момента инерции: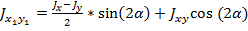

Главные оси, главные моменты инерции. Определение направления главных осей. Определение значения главных моментов инерции.

Оси, относительно которых центробежный момент инерции сечения обращается в нуль, называются главным осями. Моменты инерции относительно главных осей инерции называются главными моментами инерции сечения. Чтобы определить положение главных центральных осей несимметричной фигуры, повернем произвольную начальную систему центральных осей z,yна некоторый угол 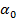при котором центробежный момент инерции становится равным нулю.

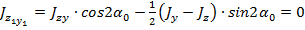, откуда .

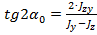Определение значений главных моментов инерции:

;

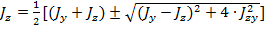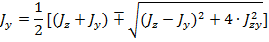
Причем верхние знаки следует брать при .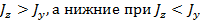

Виды напряженного состояния. Тензор напряжений. Закон парности касательных напряжений.

Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по всем площадкам, содержащим точку.

Линейное – если одно главное напряжение отлично от нуля, а 2 других равны 0.

Плоское – если 2 главных напряжения отличны от нуля, а одно равно нулю.

Объемное – если все 3 главных напряжения отличны от нуля.

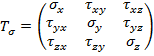– тензор напряжений.

Закон парности касательных напряжений: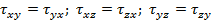

Плоское напряженное состояние. Напряжения по наклонным площадкам. Определение напряжений с помощью кругов Мора. Прямая и обратная задача.

Плоским называется напряженное состояние, при котором одно из трех главных напряжений равно нулю.

Напряжения по наклонным площадкам: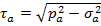

Определение напряжений с помощью кругов Мора: ;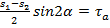

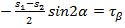
Координаты точек круга соответствуют нормальным и касательным напряжениям на различных площадках. Откладываем от оси 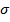из центра С луч под углом 2 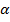( 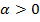, то против часовой стрелки), находим точку D, координаты которой: 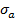, 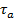. Можно графически решать как прямую, так и обратную задачи.

Прямая задача: , ,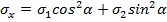

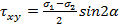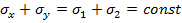
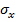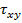Определим напряжения и , действующие по любой наклонной площадке 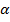по известным главным напряжениям 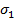и .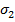

Обратная задача: ,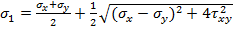

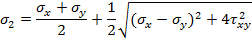
По известным нормальным касательным напряжениям, действующим в двух взаимно перпендикулярных площадках, найти главные (max и min, 1и 2) напряжения и положение главных площадок. Касательные напряжения по главным площадкам равны 0). Угол 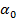определяющий положение главных площадок: 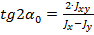. Если одно из главных напряжений окажется отрицательным, то их надо обозначить 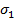, , 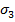если оба отрицательны, то , .

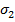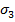Косой изгиб. Определение напряжений, условие прочности.

Изгиб с кручением стрежней круглого поперечного сечения. Определение расчетного напряжения и проверка прочности.

σ=√(Mx^2+My^2)/Wно; τ=Mкр/Wρ; По четвертой энергетической теории: σmax^IV=√(σ^2+3*τ^2)

Внутренние силовые факторы. Метод сечений. Понятие о напряжениях. Связь между внутренними силовыми факторами и напряжениями.

Чтобы найти внутренние силы воспользуемся методом сечений РОЗУ. Р – разрезаем произвольный плоскостью на А и В. О – отбрасываем одну из этих частей, например В. Рассмотрим оставшуюся часть. З – заменяем. Внутренние силы мы заменяем главным вектором и главным моментом. Раскладываем главный вектор и главный момент в плоскости на оси. Внутренние силовые факторы:

Qx, Qy –вызывают сдвиг – перерезывающие поперечные силы; N – нормальная продольная шина, растяжение, сжатие бруса; Mz – крутящий момент; Mx, My – изгибающий момент. График изменения внутренного фактора при передвижении вдоль оси стержня называется эпюрой. У – уравновешиваем.

Выделим в рассматриваемом сечении точку B, а в окрестности этой точки – элементарную площадку с площадью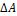 . Пусть 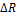– равнодействующая всех внутренних сил, действующих на площадке. Отношение 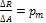называется средним напряжением на площадке 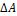, которое характеризует среднюю интенсивность распределения внутренних сил на этой площадке. Предел этого отношения 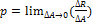называется полным напряжением в точке B. Это напряжение можно разложить на составляющие: нормальное и касательные к плоскости сечения. Нормальная составляющая 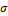называется нормальным напряжением; составляющая, лежащая в плоскости сечения, называется касательным напряжением 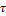. Касательную составляющую раскладывают на 2 перпендикулярные составляющие вдоль осей x и y - 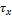и 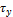. Величина полного напряжения 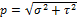. Связь напряжений с внутренними силовыми факторами может быть описана следующимисоотношениями: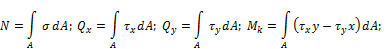 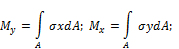2. Растяжение и сжатие. Напряжение. Деформация. Условия прочности и жесткости.Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы, а прочие силовые факторы равны нулю. Деформацией называется изменение формы и размеров тела под действием напряжений. Напряжение - сила, действующая на единицу площади сечения детали.Условие прочности: 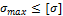, условие жесткости: 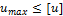.3. Механические характеристики материалов. Испытание материалов на растяжение сжатие. Под механическими характеристиками подразумеваются значения напряжений и деформаций, соответствующие определенным точкам на диаграмме условных напряжений.Пределом пропорциональности 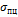называется наибольшее напряжение, до которого деформации прямо пропорциональны напряжениям.Пределом упругости 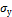называется напряжение, до которого материал не получает остаточных деформаций.Пределом текучести 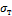называется напряжение, при котором деформации растут без заметного увеличения нагрузки.Пределом прочности 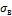называется максимальное напряжение, выдерживаемое материалом при растяжении. Пределом упругости считается напряжение, при котором остаточные деформации достигают заранее установленной величины.4. Геометрические характеристики плоских сечений. Определение центра тяжести сложных сечений. Геометрические характеристики – числовые величины, определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции.

Центр тяжести сложного сечения определяется из условия