Действующие значения переменных токов и напряжений.

За основу для измерения переменного тока положено сопоставление его среднего теплового действия с тепловым действием переменного тока. Определенное посредством такого сравнения значение силы тока наз-ся действительным значением . Если измерительный ток периодически изменившись нагревает некоторое сопротивление так, как его нагревал постоянный ток с силой 5А, то действующее значение такого переменного тока 5А.Постоянный ток за время Т выдает Qтепл=I^2rT,{Дж}

Переменный ток за это же время Qтепл=₀∫^Т i^2rdt, {Дж}

где -i мгновенное значение переменного тока.

По определению действующего значения постоянный ток выделил такое же Qтепл, след-но:

I^2rT = ₀∫^Т i^2rdtна основании чего искомое значение действительного тока

I= √1/T*₀∫^Т i^2dt,. Таким образом действительное значение тока определяется как среднее квадратное за период значения переменного тока

I=√(1/T)*₀∫^Т I_m^2*sin^2(ωt)dt= I_m√(1/T)* ₀∫^Т (1-cos2 ωt)/2 dt

Так как

₀∫^Т dt= T, а ₀∫^Т cos2 ωt dt=0, то I= I_m /√ 2

Значит действительное значение переменного тока меньше нго амплитудного значения в √ 2раз. Также можно определить действительное значение меременного напряжения по аналогии. Действительное значение было выбрано в качестве основной характеристики переменного тока из-за того что в большинстве случаев действие тока пропорционально квадрату силе тока.

15.Закон Ома для простейших цепей переменного тока.Величина и начальная фаза переменного тока создаваемого переменным напряжением зависит не только от величины сопротивления образующую цепь, но и от индуктивности и емкости этой цепи. 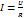закон Ома для цепи переменного тока или части цепи содержащей только сопротивление R. 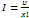закон Ома для цепи переменного тока или части цепи содержащей только индуктивность L. 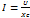закон Ома для цепи переменного тока или части цепи содержащей только емкость C.

16. Элементы электрических цепей переменного тока.В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R ,индуктивностью L и емкостью С. В технике часто встречаются цепи переменного тока, в которых преобладает один или два из этих параметров.
Цепь с активным сопротивлением
Активным сопротивлением R обладают проводники и элемен­ты, которые нагреваются при прохождении через них тока.
Если к активному сопротивлению R (рис. 4.7, а) приложено синусоидальное напряжение u=U_msin wt, то и ток в этой цепи изменяется по синусоидальному закону:

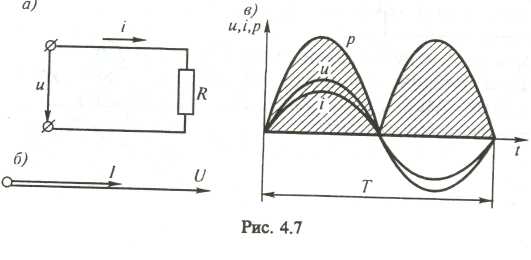
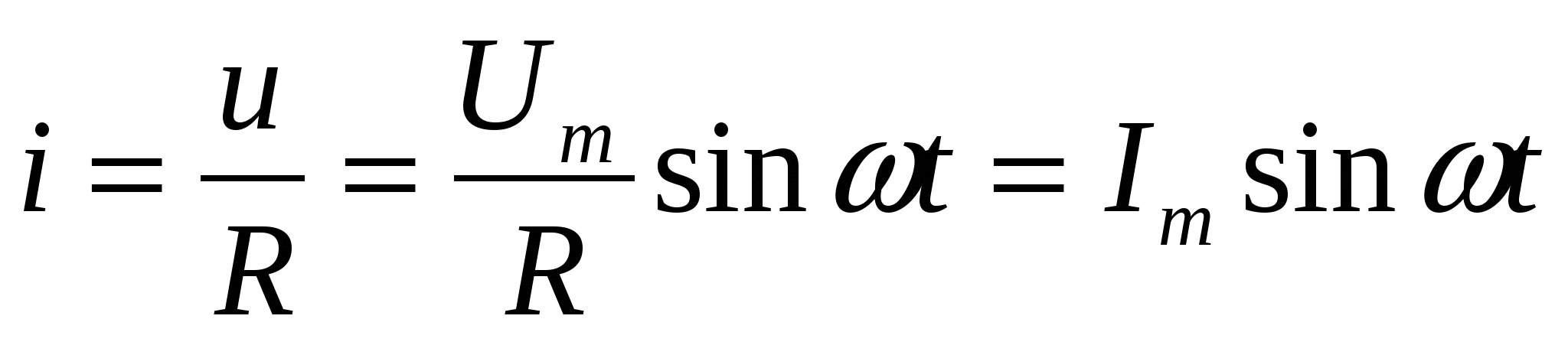
где
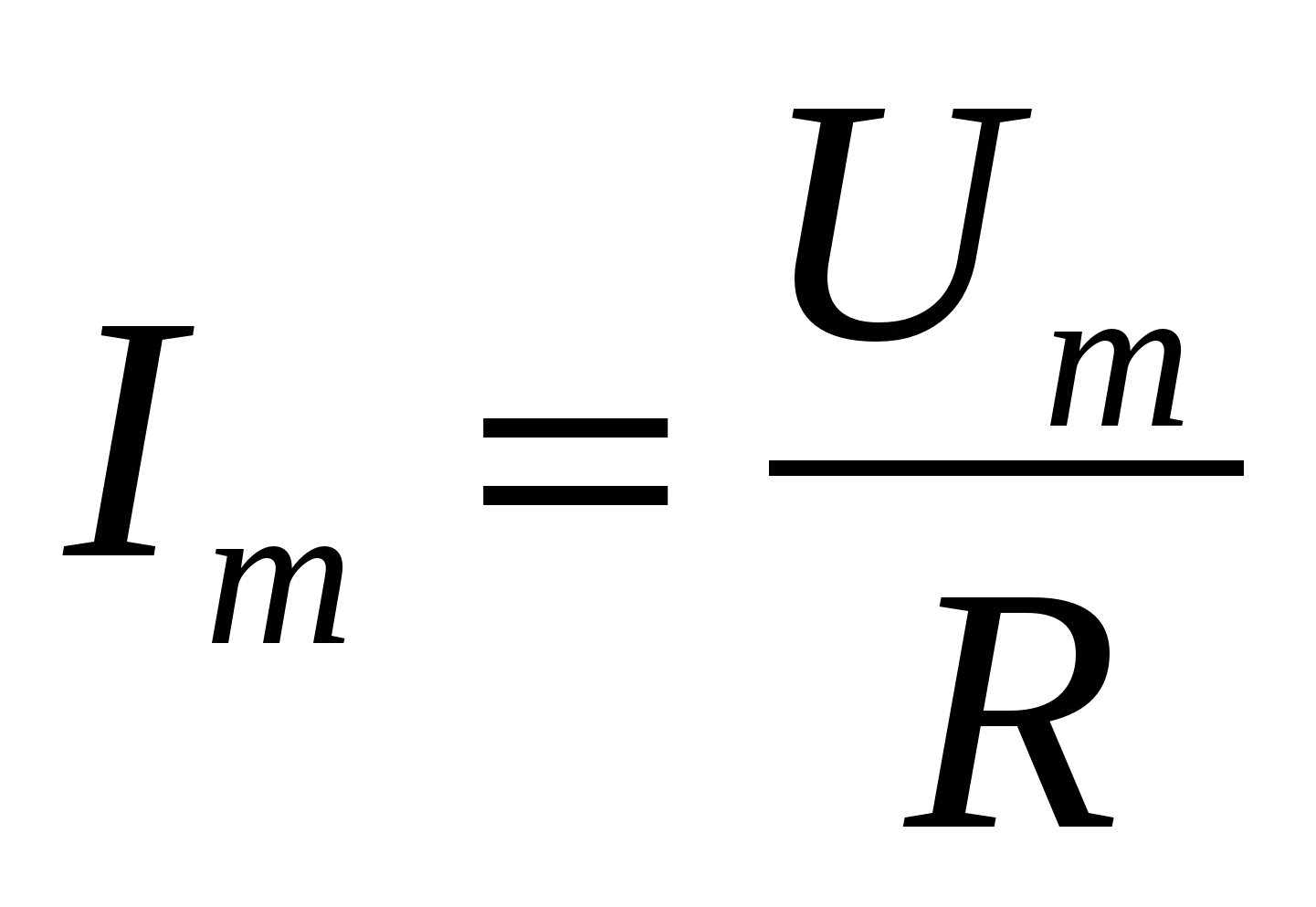(4.13)

Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны. Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 4.7, б, а волновая — на рис. 4.7, в.
Математическое выражение закона Ома для цепи перемен­ного тока с активным сопротивлением:
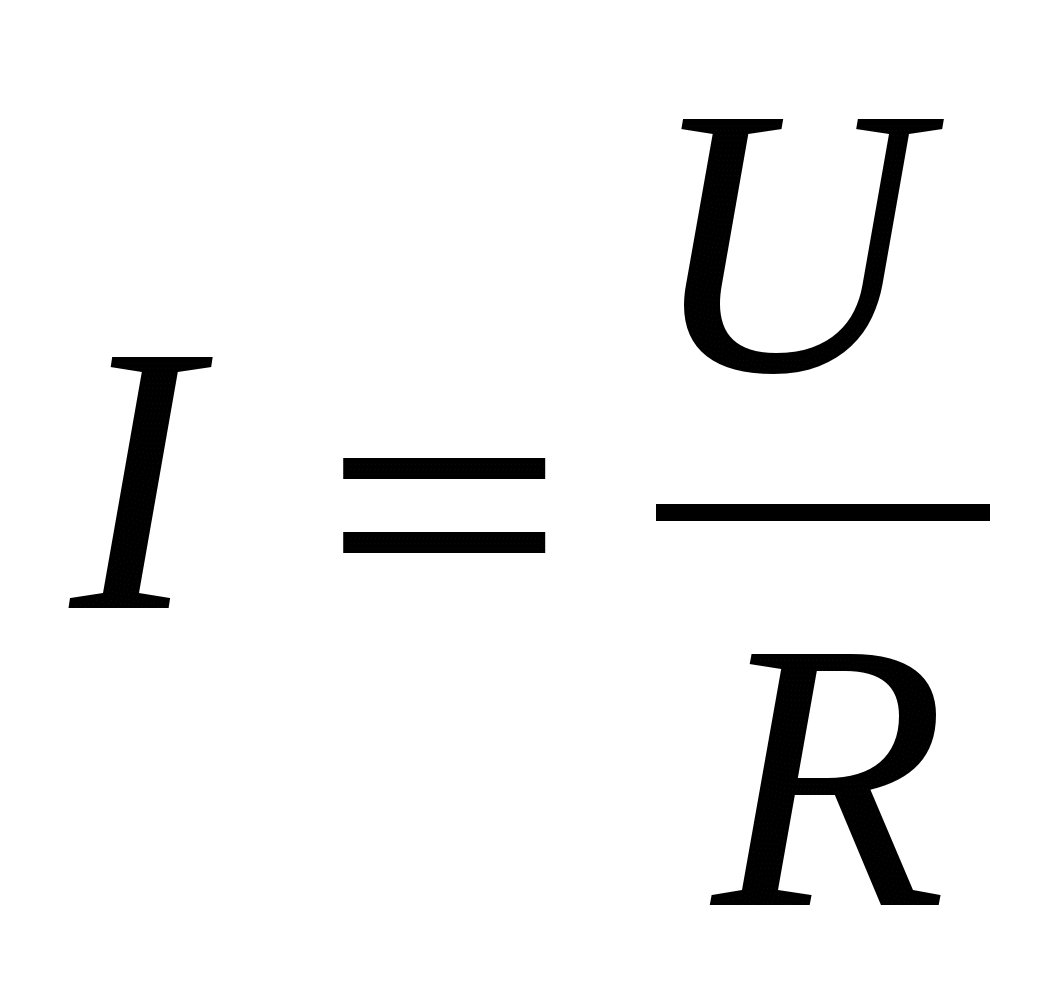(4.14)
Это вытекает из выражения (4.13), если левую и правую часть уравнения разделить на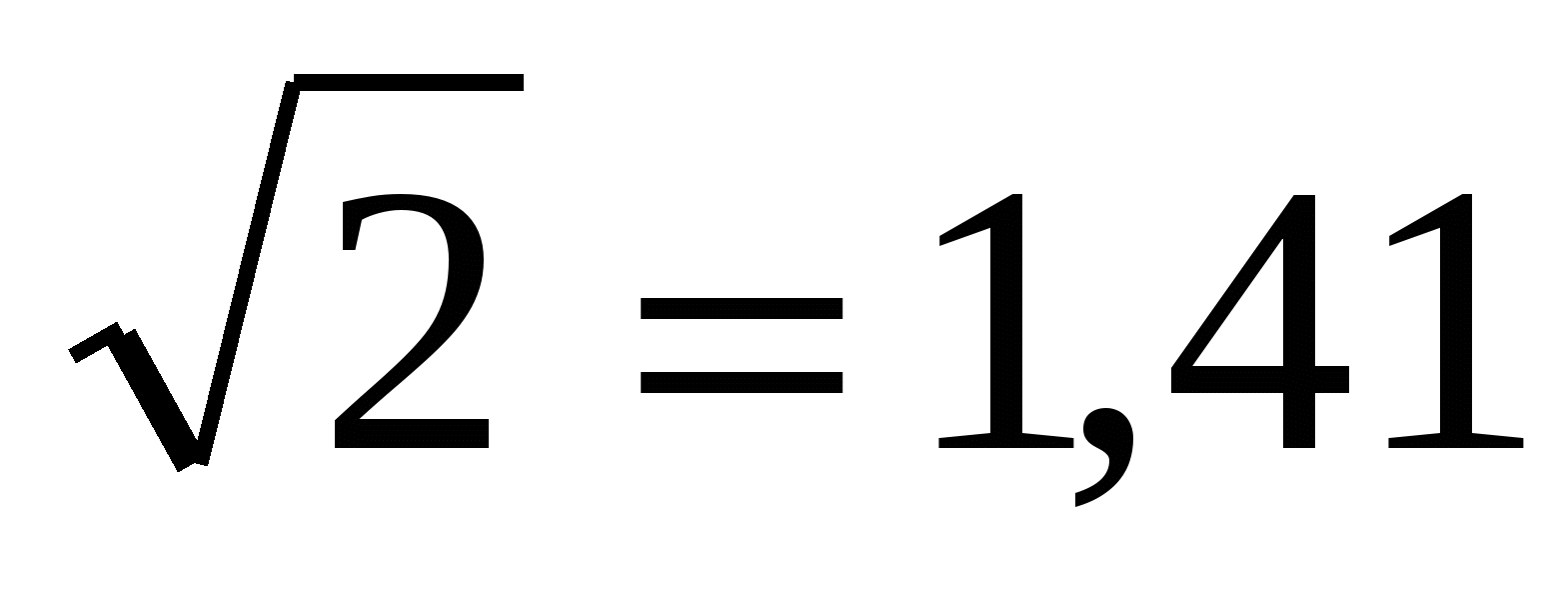
Мгновенная мощность цепи p = ui. Если произвести это дейст­вие над кривыми тока и напряжения в определенном масштабе (рис. 4.7, в), то получим волновую диаграмму мощности р.
Как видно из волновой диаграммы, мощность в цепи с ак­тивным сопротивлением изменяется по величине, но не изме­няется по направлению. Эта мощность (энергия) необратима.
От источника она поступает к потребителю и преобразуется в другие виды мощности (энергии). Эта мощность полностью потребляется. Такая мощность называется активной.
Сопротивление R, на котором происходит такое преобразова­ние, называется активным сопротивлением.
Величина активной мощности Р в цепи (рис. 4.7, а)
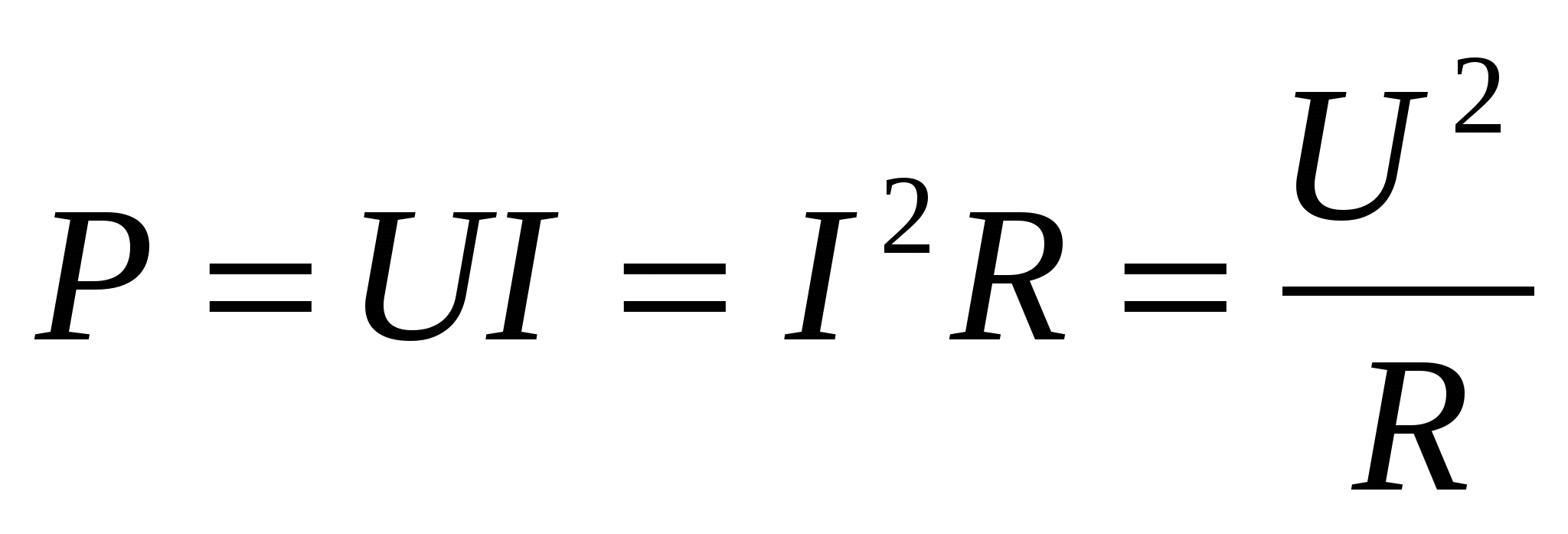(4.15)
Измеряется активная мощность в ваттах (Вт). Активная мощность характеризует среднюю скорость преоб­разования электрической энергии в другие виды энергии.
Цепь с индуктивностью
Катушка с индуктивностью L, у которой R=0 и С=0, назы­вается идеальной. Если в цепи с идеальной катушкой (рис. 4.8, а) проходит синусоидальный ток i=I_mt, то он создает синусо­идальный магнитный поток ф=Фwsin_mt, который индуктирует в катушке ЭДС самоиндукцииwsin
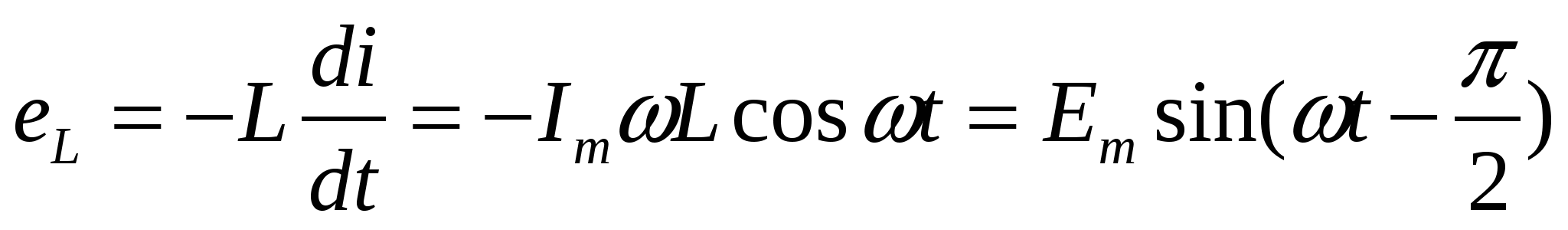, (4.16)
где E_m=I_mL).wL (или E=Iw
Для существования тока в идеальной катушке к ней должно быть приложено напряжение, которое в любой момент времени равно по величине (u=-e_L), но находится в противофазе с ЭДС самоиндукции, т.е.
,
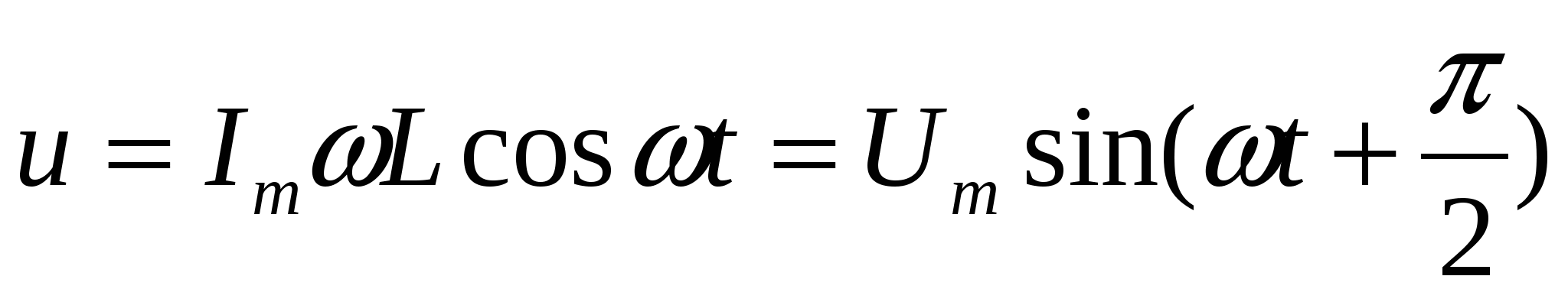где U_m=I_mL).wL (или U=Iw
Векторная диаграмма для цепи с идеальной катушкой изоб­ражена на рис. 4.8, б, а волновая — на рис. 4.8, в.

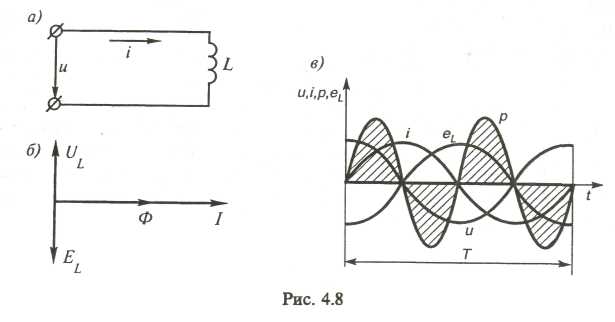
Напряжение, приложенное к идеальной катушке, опережает ток по фазе на угол /2=90°.p
Тогда математическое выражение закона Ома для этой цепи: Действующее значение напряжения, приложенного к идеаль­ной катушке, U=I*wl. Тогда математическое выражение закона Ома для этой цепи:
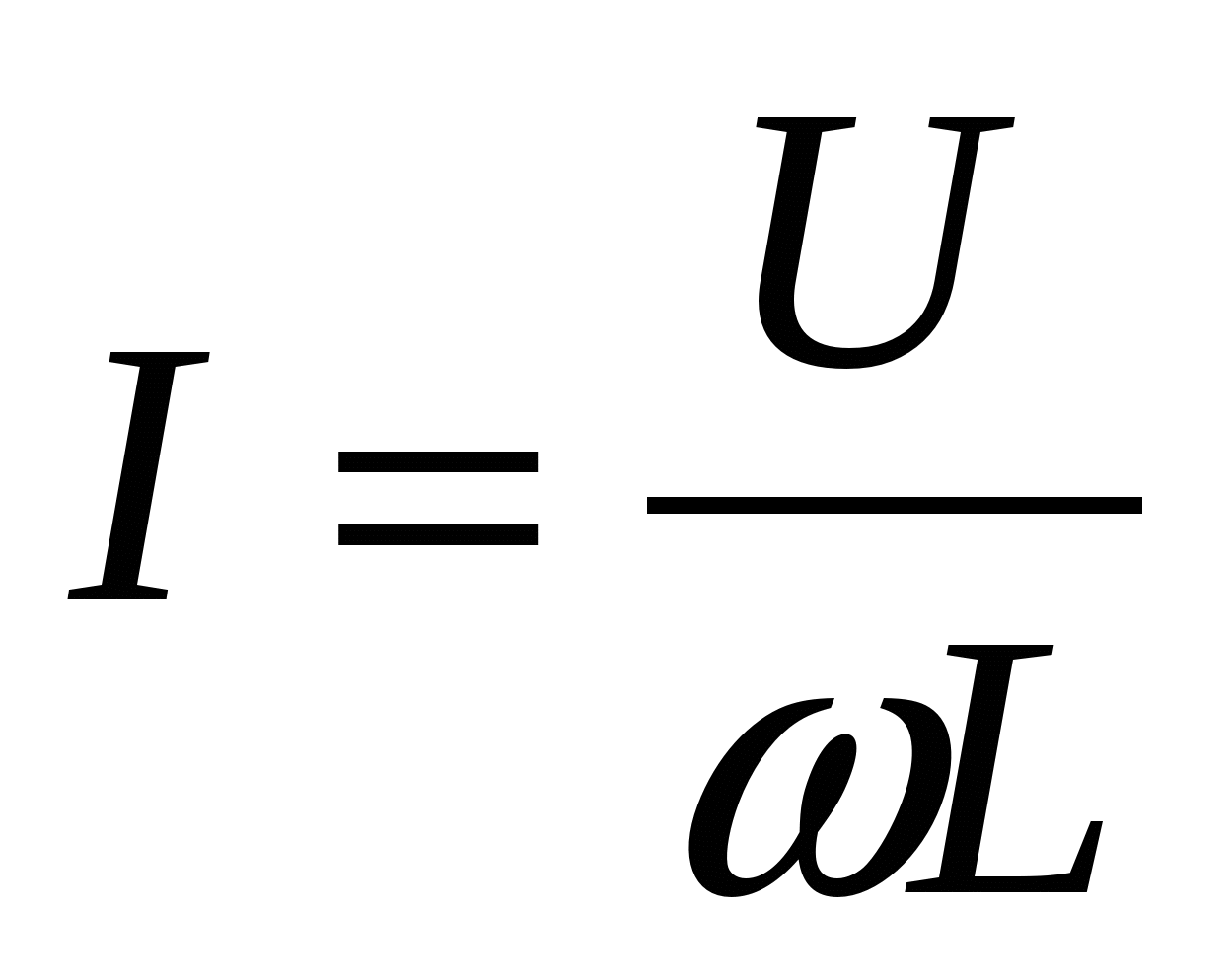(4.18)
L имеет размерность сопро­тивления и называетсяwЗнаменатель этого выражения индуктивным сопротивлением
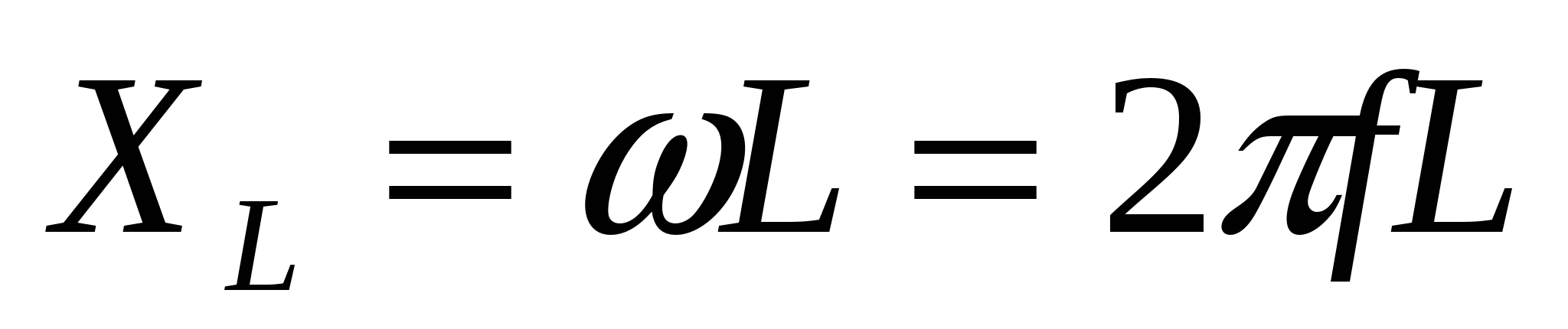(4.19)
Мгновенная мощность для цепи с идеальной катушкой индук­тивности
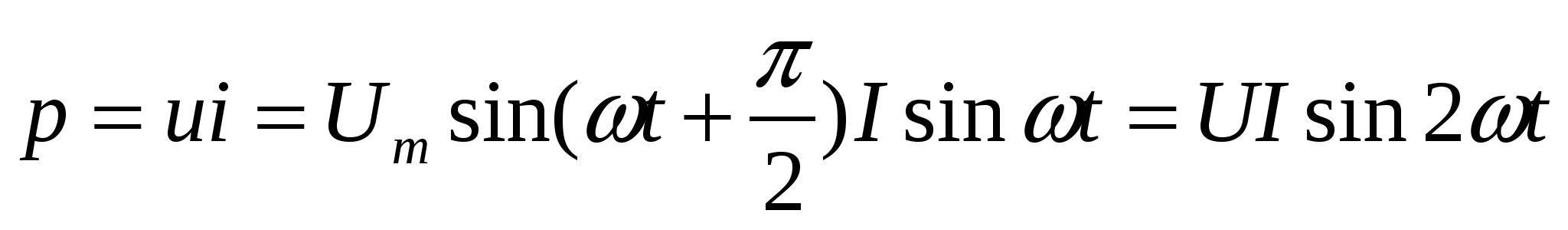(4.20)
В цепи с идеальной индуктивностью (4.20) мощность изменя­ется по синусоидальному закону с двойной частотой. Это следует и из волновой диаграммы мощности (рис. 4.8, в), т. е. в 1-ю и 3-ю четверти периода мощность (энергия) накапливается в магнит­ном поле идеальной катушки, а во 2-ю и 4-ю четверти периода та же мощность (энергия) из магнитного поля возвращается к ис­точнику. Таким образом, в цепи переменного тока с индуктив­ностью имеет место колебание мощности (энергии) между источ­ником и магнитным полем индуктивности. Такая колеблющаяся между источником и нагрузкой мощность, в отличие от актив­ной, называется реактивной мощностью:
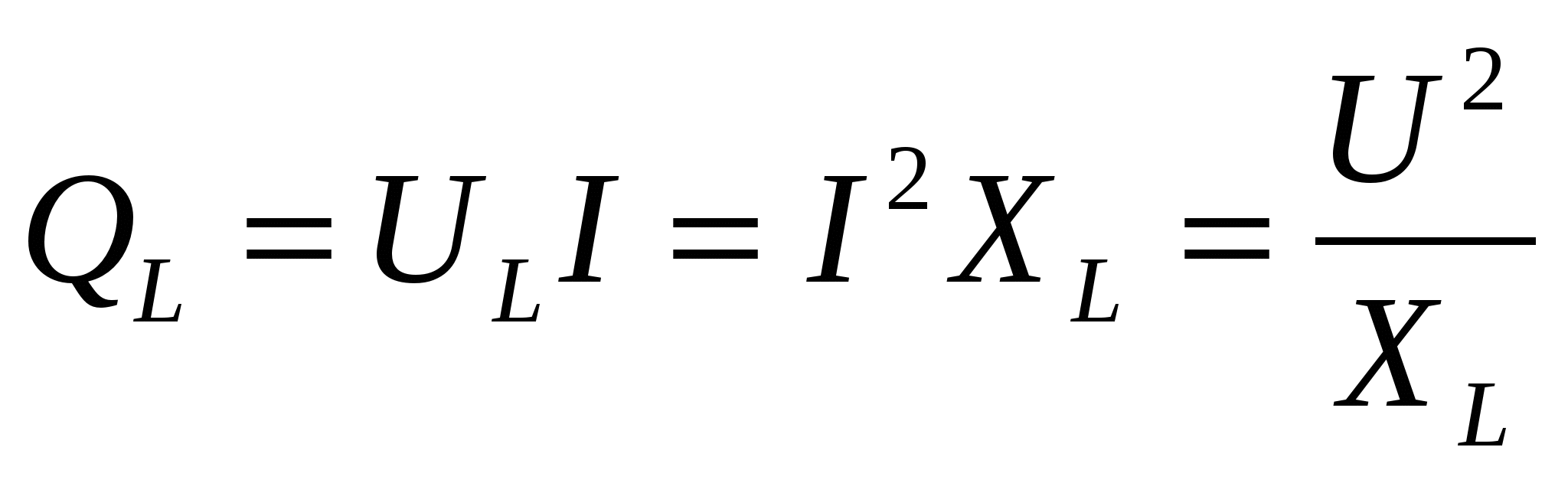(4.21)
Измеряется реактивная мощность в варах (вар). Реактивная мощность загружает источник и провода, но не потребляется, т. е. не преобразуется в другие виды мощности (энергии).
Максимальное значение энергии, накапливаемой в магнитном поле катушки,
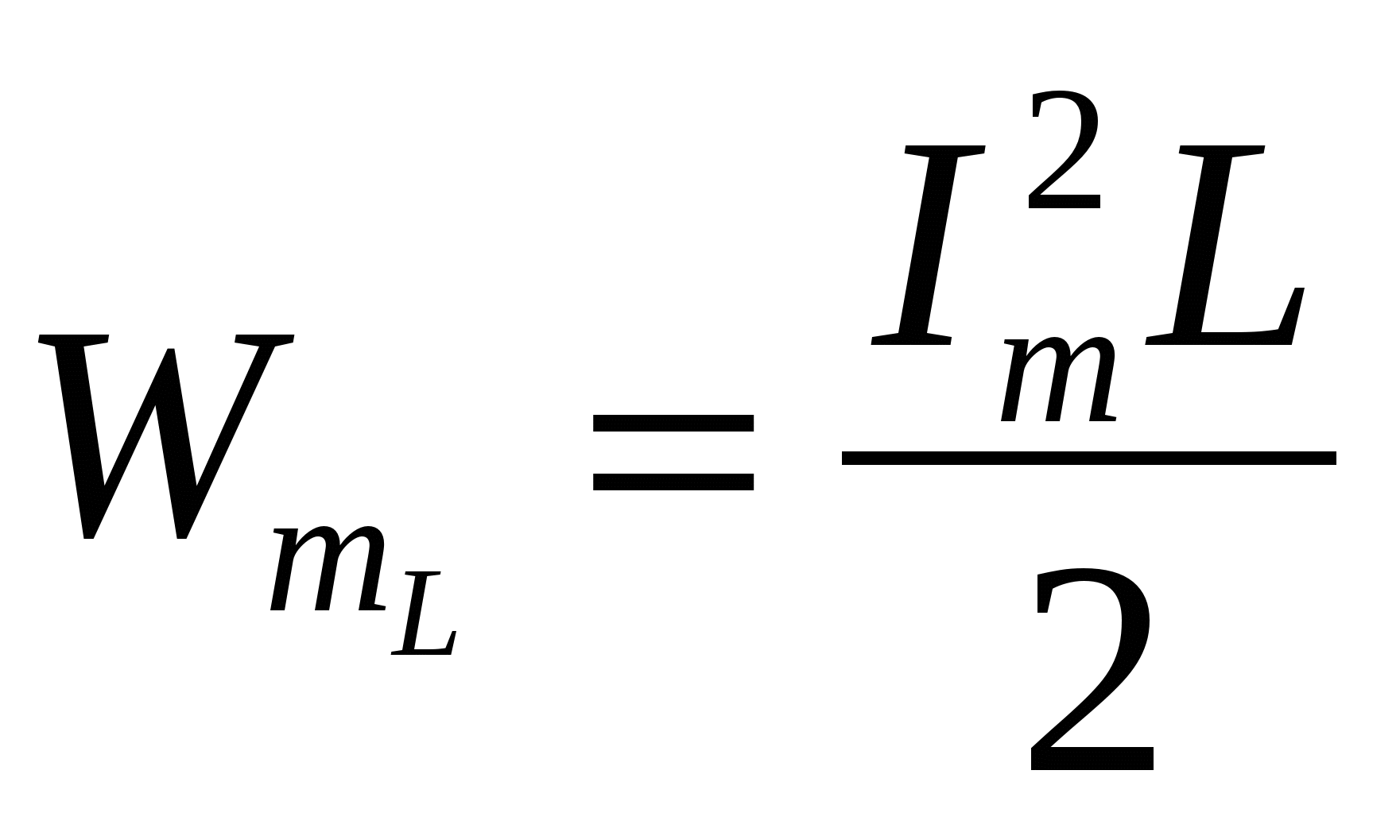(4.22)
Так как реактивная мощность Q_L имеет место на индуктивном сопротивлении, то индуктивное сопротивление называют реак­тивным X индуктивного характера (X_L).
Индуктивное сопротивление обусловлено противодействием ЭДС самоиндукции изменению тока (правило Ленца).
Цепь с емкостью.
Если к конденсатору емкостью С приложено переменное на­пряжение u то в цепи конденсатора возникает пере­менный ток зарядки и разрядки конденсатора. Через диэлектрик конденсатора ток не проходит.

Если напряжение на конденсаторе изменяется по синусоидаль­ному закону u=U_msinwt, то ток в цепи конденсатора
,
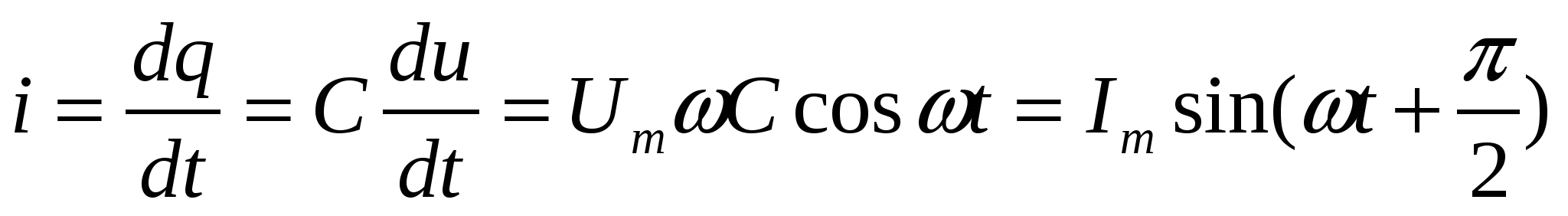где I_m=U_mC, т. е. ток в цепи с емкостью С опережает напряже­ние на угол w/2 = 90°
Векторная диаграмма для цепи с емкостью изображена на рис. 4.9, б, а волновая — на рис. 4.9, в.
Математическое выражение закона Ома для цепи переменного тока с емкостью С:
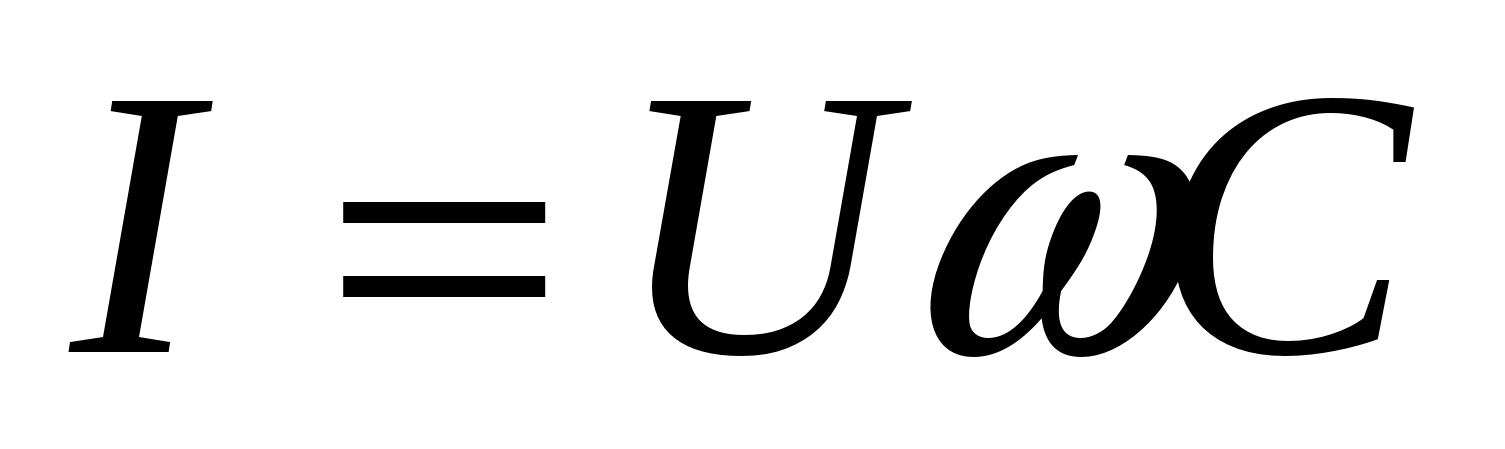или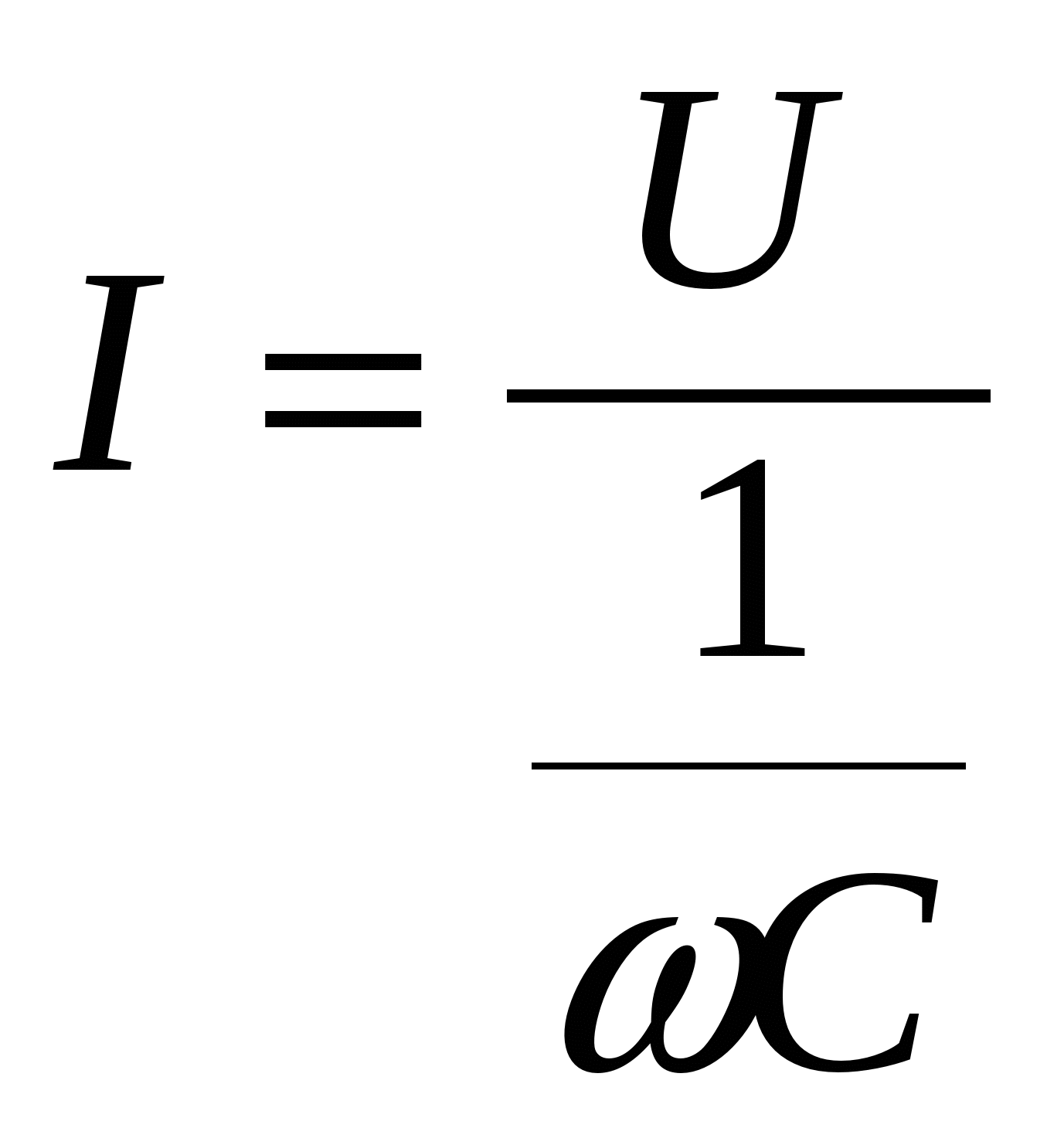
С имеет размерность сопротивления и называетсяwЗнаменатель этого выражения 1/ емкостным сопротивлением

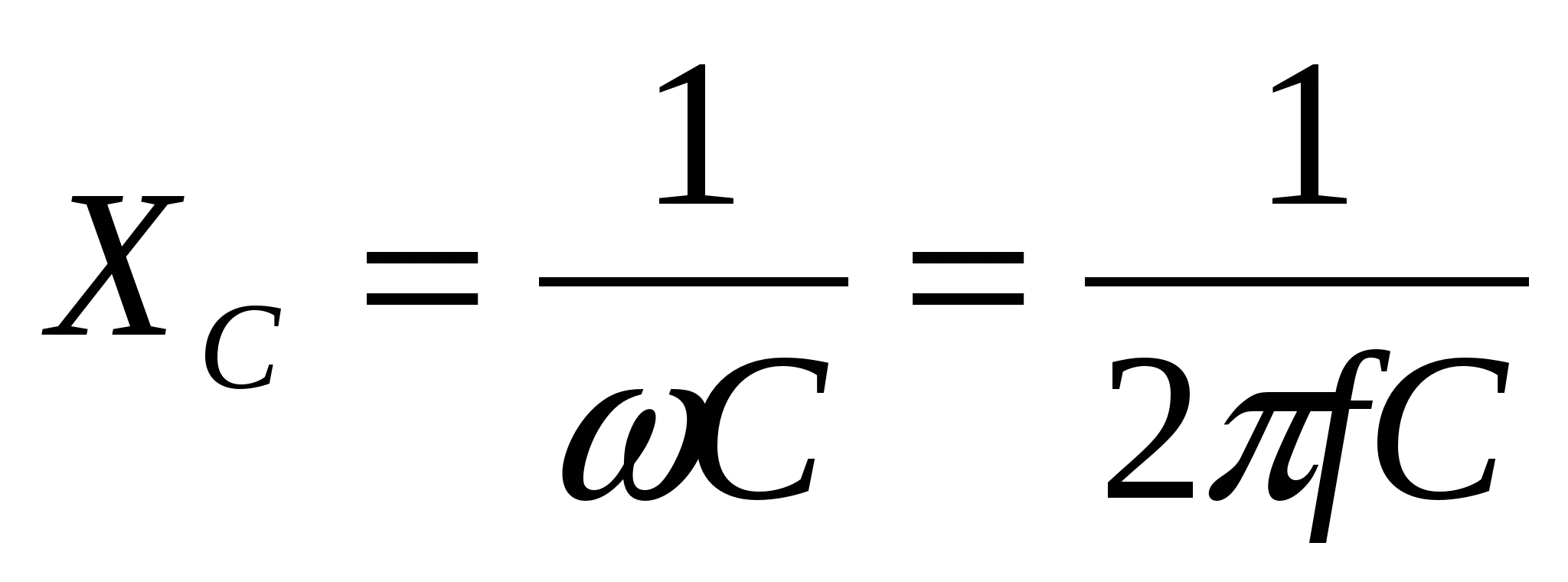
Мгновенная мощность для цепи с емкостью:

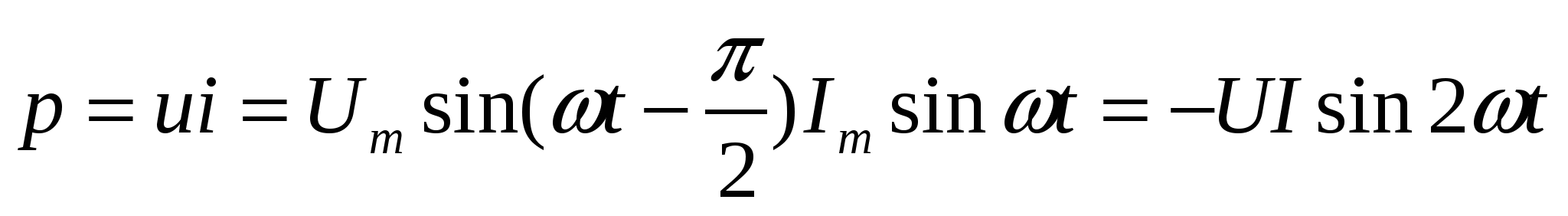
т. е. мгновенная мощность р изменяется по синусоидальному закону с двойной частотой. Это следует также из волновой диаграммы мощности (рис. 4.9, в), т. е. во 2-ю и 4-ю четверти периода мощность (энергия) накапливается в электрическом поле конденсатора, а в 1-ю и 3-ю четверти периода та же мощность (энергия) возвращается к источнику. Таким образом, в цепи переменного тока с емкостью происходит колебание мощности (энергии) между источником и электрическим полем конденсато­ра, т.е. эта мощность реактивная

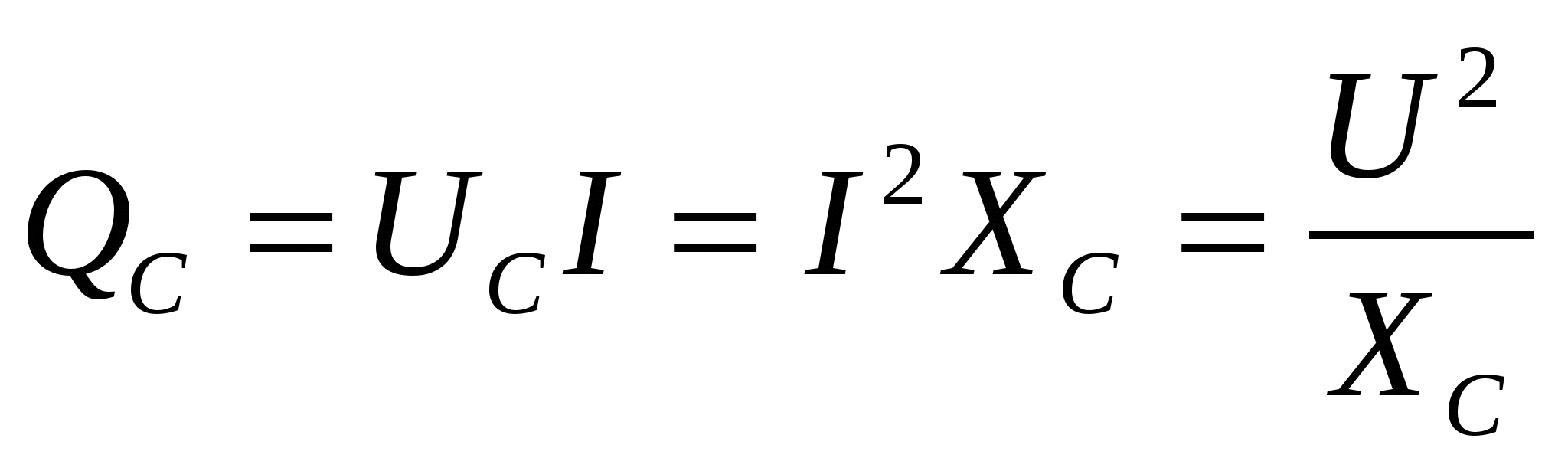
Из волновой диаграммы видно, что реактивная мощность в цепи с емкостью находится в противофазе с реактив­ной мощностью в цепи с индуктивностью (рис. 4.8, в), поэтому перед аналитическим выражением мгновенной мощности в цепи с емкостью (4.25) стоит знак «—».
Так как реактивная мощность связана с емкостным сопротив­лением, то емкостное сопротивление называют реактивным X, емкостного характера (Х_С).
Максимальное значение энергии, накапливаемой в электрическом поле конденсатора:
.
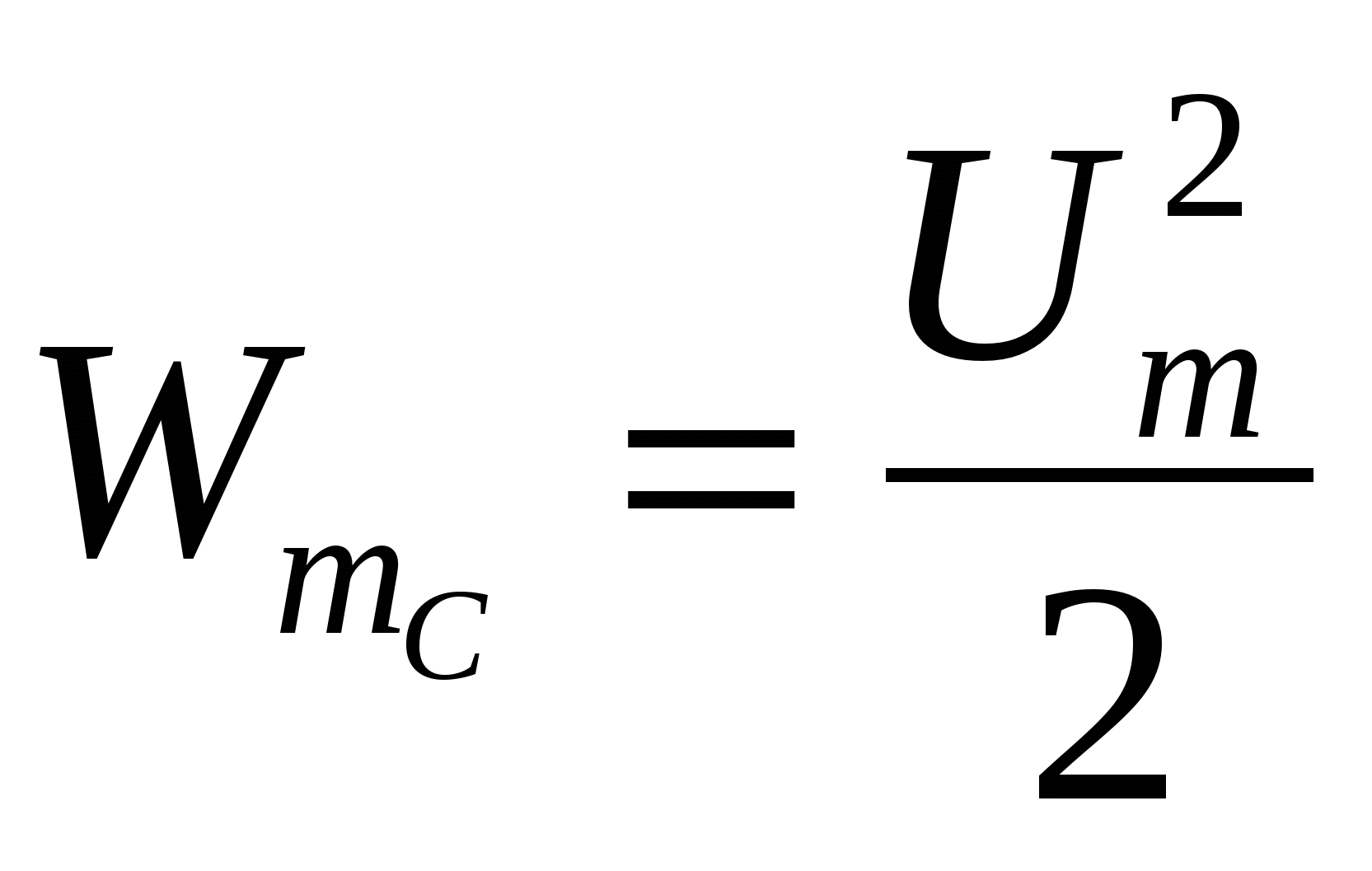