Узел, контур, ветвь, схема замещения
Узел, контур, ветвь, схема замещения
Ветвью называется один или несколько соединенных последовательно элементов заключенных между двумя узлами в которых протекает один ток. Ветви соединенные между двумя узлами образуют парал-е соединение.
Узел – место соединения трех или большего числа ветвей
Контур – замкнутая часть цепи проходящая по нескольким ветвям. Контуры, которые отл-ся хотя бы одной ветвью называются независимыми.
За положительное направление токов принято считать движение положительных зарядов поэтому ток пассивных элементов протекает от точки с большим потенциалом к точке с меньшим, в активных - наоборот, что соответствует определению ЭДС, как величины, характерезующей способность стороннего поля вызывать эл. ток во внешней цепи заданного направления.
3.а) Закон Омаустанавливает связь между напряжением тока и сопротивлением.
I =U /R для пасивного элемента
Для участка цепи пасивного элемента положительной направление тока, например, от т.1до т.2, т.е. от большего потенциала к меньшему напряжение будет равно:
U1,2=-E1+IR
I= (U1,2 +- E1)/R
Знак перед ЭДС определяется взаимным направлением тока и ЭДС.При совпадении направлений, ЭДС берут «+», в противном случае – «–»
б) Закон Ома замкнутой цепи с источником ЭДС

I = E/(Ru+Rл+Rн)
E = IRu+IRл+IRн
IRu – падение напряжения на источнике
IRл – падение напряжения внутри линии
IRн – падение напряжения нагрузки
в) Внешняя характеристика
Uu=E- ∆Uн

W=I2Rt; W-кол-во преобразующ. Энергии
P=I2R=U2/R=UI
законДжоуля-ЛенсаQ=A=I2Rt
Баланс активной мощности
Активная мощность, развиваемая источником равна сумме мощностей потребляемых всеми приемниками
EI=I2Ru+I2Rл+I2Rн
∆Ru-мощность, расходующаяся на нагрев ание источника
∆Rл – мощность, на нагревание линии передач
∆Rн – мощность, потребляемая нагрузкой
Pэ= ∆Pu+∆Pл+∆Рн
Законы Кирхгофа.
Соотношение между токами ЭДС в ветвях эл. цепи и напряжением на элементах определяется 2-мя законами Кирхгофа.
1 закон. Устанавливает законбаланса тока в разветвленной эл. цепи.
Алгебраическая сумма токов сходящихся в узле равно 0.
∑I=0 I1+I2+I3+I4=0
Либо сумма входящих равнасумме исходящих. I1+I2+I3=I4
2 Закон. Алгебраическая сумма ЭДС в контуре равна алгебраической сумме падений напряжений наэлементах этого контура.
∑E=∑U=∑IR
 Выбираем направление отхода контура по часовой стрелки.
Выбираем направление отхода контура по часовой стрелки.
ЭДС совпадающая с направлениес отхода контура – «+», в противном случае – «–»
E1-E2- I1R1+ I2R2 + I3R3 -I4R4=0
В графич. виде подтверждение закона Кирхгофа яыляется диаграмма.
Зависимость потенциалов контура от сопротивлений.


5. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла.
При последовательном соединении проводников сила тока в любых частях цепи одна и та же: I= I1=I2
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: U= U1+U2+ U3+U4
А сопротивление R= R1+R2+R3+R4
U= U1+U2+ U3+U4= I1R1+ I1R2+ I1R3+ I1R4=I1(R1+R2+R3+R4) = I1Rэкв .
P= I2Rэкв
При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединённых проводниках: I= I1+I2
Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же:
U= U1=U2
Сопротивление 1/R= 1/R1+1/R2+1/R3…..
g=1/R
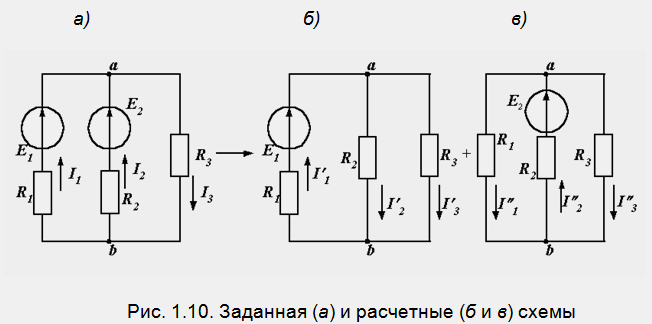
Метод наложения
В основе метода лежит принцип суперпозиции (наложения): ток в любой ветви сложной электрической цепи, содержащей несколько ЭДС, может быть найден как алгебраическая сумма токов в этой ветви от действия каждой ЭДС в отдельности.
При расчете схемы, содержащей несколько ЭДС поочередно полагают равную нулю всей ЭДС кроме одной.
Например, токи в схеме на рис. 1.10, а находятся как алгебраические суммы частичных токов, определяемых из схем 1.10, б и в.
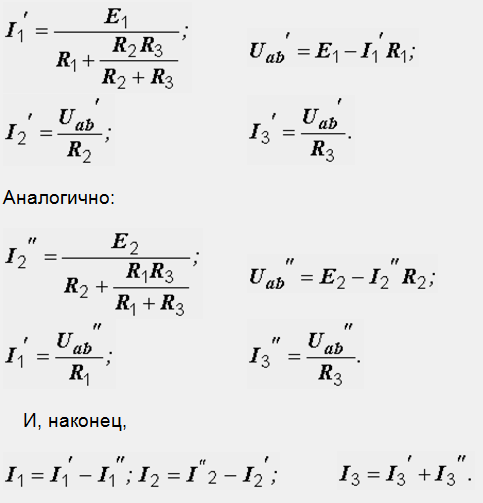
Метод контурных токов
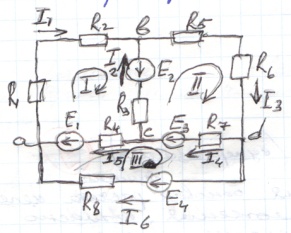 При расчете сложных цепей с большим числом узловых точек предпочтителен метод контурных токов, который позволяет освободиться от составления уравнений по первому закону Кирхгофа, тем самым ,сократив общее число совестно решаемых уравнений. Суть метода рассмотрим на примере:
При расчете сложных цепей с большим числом узловых точек предпочтителен метод контурных токов, который позволяет освободиться от составления уравнений по первому закону Кирхгофа, тем самым ,сократив общее число совестно решаемых уравнений. Суть метода рассмотрим на примере:
Разбиваем схему на 3 смешных независимых контуров.Выбираем условно (+) направление обхода в них. В ветвях яв-ся общ для 2-х смежных контуров протекающие токи равны алгебр.сумме 2-х контурных токов. Применим для каждого контура в отдельности 2 закон Кирхгофа и получим систему уравнений равную числу контурных токов.
E1+E2=Iк1(R1+R2)+(Iк1-Iк2)R3+(Iк1-Iк3)R4
E3-E2=(Iк2-I1)R3+Iк2(R5+R6)+(Iк2-Iк3)R7
E4-E1-E3=Iк3R8+(Iк3-Iк1)R4+(Iк3-Iк2)R7
Входящие в эти уравнения контурные токи удовлетворяют 1З.К. во всех точка разветвления. Полученные ур-я можно представить в виде более удобном для совместного решения:
E1+E2=Iк1(R1+R2+R3+R4)-Iк2R3-Iк3R4
E3-E2=-Iк1R3+Iк2(R3+R5+R6+R7)-Iк3R7
E4-E1-E3=-Iк1R4-Iк2R7+Iк3(R4+R7+R8)
Решая полученную систему рекомендуется метод Крамера. Найдем контурные токи по которым определим токи в ветвях
I1=Ik1
I2=Ik2-Ik1
I3=Ik2
I4=Ik2-Ik3
I5=Ik1-Ik3
I6=Ik3
Получение переменного тока.
Переменный ток создается генераторами переменного тока, в которых электродвижущая сила (ЭДС) возникает в результате процесса электромагнитной индукции. В цилиндрической полости, изготовленной из мягкой стали, вращается постоянный магнит, называемый ротором. Неподвижный сердечник с его обмоткой называется статором. Статор и ротор изготовлены так, что магнитная индукция B в зазоре между ними изменяется по закону:
B = Bmcos(wt),
где Bm – максимальное значение вектора электромагнитной индукции.
Магнитный поток через контур катушки равен:
Фm = B*S = Bm*S*cos(wt).
В обмотке статора при изменении магнитного потока наводится ЭДС, равная
ei = - dФ/dt = Bm*S*sin(wt) = emsin(wt).
Итак, напряжение, получаемое с помощью генераторов переменного тока, изменяется по гармоническому закону:
U = Umsin(wt).
Ток в электрических цепях изменяется аналогичным образом:
I = Imsin(wt + f).
Активная мощность
Потребляемая в цепи мощность равна произведению напряжения на зажимах это цепи на силу тока. При переменном напряжении это справедливо только для мгновенной мощности выражаемое через мгновенные значения напряжения и силы тока.
p=ui
Переодические изменения напряжения и силы тока вызывают переодическое изменения мгновенной мощности. Следовательно, мощность – величина переодически изменяющаяся, малоудобная для оценки энергетического состояния цепи, поэтому для этого основной величиной является средняя мощность. Эту мощность измеряет вольтметр. Обозначается – [p].
Для цепи синусоидального тока выразим через действующие значения напряжения и тока. Если в общ. случае напряжение на зажимах цепи опережает некоторый ток на угол φ, т.е.:
u=Umax(sinwt+φ), i=Imaxsinwt
то активная мощность будет равна:
p= 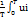 dt =
dt = 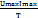 (cosφ
(cosφ 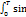 2wtdt+sinwtcoswtdt)
2wtdt+sinwtcoswtdt)
Заменив sin2wt = (1-cos2wt)/2 и sinwtcoswt=sin2wt/2, получим:
p = 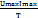 (
( 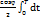 -
- 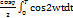 + sin
+ sin 
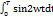 )
)
2 и 3 интегралы в скобках = 0, т.к. это интеграл за целое число периодов.
Заменив Амплитуду через действующее значение получим основную формулу мощности
p=uicosφ
cosφ – коэффициент мощности. Чем меньше – тем хуже исполюзуется энергетическая установка.
Резонанс напряжения
Резонанс напряжений

Если  , то ток в цепи,
, то ток в цепи,  то есть цепь в данном случае имеет наименьшее сопротивление, как будто в цепи присутствует только активная нагрузка r. При этом напряжения на индуктивности и емкости
то есть цепь в данном случае имеет наименьшее сопротивление, как будто в цепи присутствует только активная нагрузка r. При этом напряжения на индуктивности и емкости 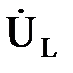 и
и 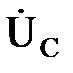 сдвинуты по фазе на π и полностью компенсируют друг друга
сдвинуты по фазе на π и полностью компенсируют друг друга
Напряжение, приложенное к цепи, равно напряжению на активном сопротивлении, и ток совпадает по фазе с напряжением. При этом напряжение на индуктивности 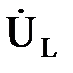 и емкости
и емкости 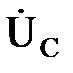 может значительно превышать входное напряжение
может значительно превышать входное напряжение  , поэтому резонанс получил название резонанса напряжений.
, поэтому резонанс получил название резонанса напряжений.
Отношение  выражает добротность контура. Добротность контура показывает, во сколько раз напряжение на индуктивном элементе превышает напряжение на входе схемы двухполюсника. В радиотехнике Q может доходить до 300 и более. Чем больше добротность, тем более острую форму имеют кривые тока и напряжений.
выражает добротность контура. Добротность контура показывает, во сколько раз напряжение на индуктивном элементе превышает напряжение на входе схемы двухполюсника. В радиотехнике Q может доходить до 300 и более. Чем больше добротность, тем более острую форму имеют кривые тока и напряжений.
Рисунок 6.4
Из условия  следует, что резонанса напряжений можно достичь, изменяя либо частоту приложенного напряжения, либо параметры цепи - индуктивность или емкость. Угловая частота ωрез, при которой наступает резонанс, называют резонансной угловой частотой:
следует, что резонанса напряжений можно достичь, изменяя либо частоту приложенного напряжения, либо параметры цепи - индуктивность или емкость. Угловая частота ωрез, при которой наступает резонанс, называют резонансной угловой частотой:  . В лаборатории резонанса напряжений достигают при ω=const, L=const, изменяя емкость С (рис. 6.4). Программа EWB позволяет наблюдать резонанс, меняя любой из перечисленных параметров.
. В лаборатории резонанса напряжений достигают при ω=const, L=const, изменяя емкость С (рис. 6.4). Программа EWB позволяет наблюдать резонанс, меняя любой из перечисленных параметров.
При резонансе напряжений можно отметить следующие моменты:
1. Резонанс напряжений происходит при условии, что входное сопротивление является чисто активным, т.е.:  , при
, при  . Ток и напряжение совпадают по фазе.
. Ток и напряжение совпадают по фазе.
2. Резонанс зависит от L, C и ω.  , или
, или  .
.
3. Напряжение источника и падение напряжения на r равны, тогда  , (
, (  ) они находятся в противофазе и взаимно компенсируют друг друга
) они находятся в противофазе и взаимно компенсируют друг друга  .
.
24. Резонанс тока ( 6 лаба)
Резонанс в цепи с параллельно соединенными элементами
(резонанс токов)
Для цепи рис. 4 имеем

 ,
,
где

В зависимости от соотношения величин  и
и  , как и в рассмотренном выше случае последовательного соединения элементов, возможны три различных случая.
, как и в рассмотренном выше случае последовательного соединения элементов, возможны три различных случая.

В цепи преобладает индуктивность, т.е.  , а следовательно,
, а следовательно,  . Этому режиму соответствует векторная диаграмма на рис. 5,а.
. Этому режиму соответствует векторная диаграмма на рис. 5,а.
В цепи преобладает емкость, т.е.  , а значит,
, а значит,  . Этот случай иллюстрирует векторная диаграмма на рис. 5,б.
. Этот случай иллюстрирует векторная диаграмма на рис. 5,б.
 - случай резонанса токов (рис. 5,в).
- случай резонанса токов (рис. 5,в).
Условие резонанса токов  или
или

Классификация приемников
Приемники, включаемые в трехфазную цепь, могут быть либо однофазными, либо трехфазными. К однофазным приемникам относятся электрические лампы накаливания и другие осветительные приборы, различные бытовые приборы, однофазные двигатели и т.д. К трехфазным приемникам относятся трехфазные асинхронные двигатели и индукционные печи. Обычно комплексные сопротивления фаз трехфазных приемников равны между собой:
Za = Zb = Zc = Zejφ.
Такие приемники называют симметричными. Если это условие не выполняется, то приемники называют несимметричными. При этом, если Za = Zb = Zc, то трехфазный приемник называют равномерным, если φa = φb = φc, то однородным.
Четырехпроводная цепь
Трехпроводная цепь
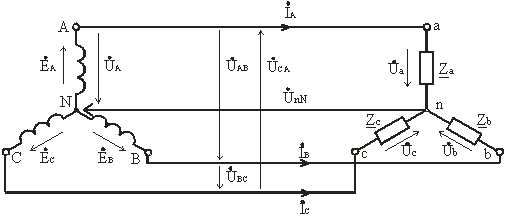
При симметричной нагрузке, когда Za = Zb = Zc = Zφ, напряжение между нейтральной точкой источника N и нейтральной точкой приемника n равно нулю, UnN = 0.
Соотношение между фазными и линейными напряжениями приемника также равно , т.е. UФ = UЛ / , а токи в фазах определяются по тем же формулам (3.12, 3.13), что и для четырехпроводной цепи. В случае симметричного приемника достаточно определить ток только в одной из фаз. Сдвиг фаз между током и соответствующим напряжением φ = arctg (X / R).
При несимметричной нагрузкеZa ≠ Zb ≠ Zc между нейтральными точками приемника и источника электроэнергии возникает напряжение смещения нейтралиUnN.
Для определения напряжения смещения нейтрали можно воспользоваться формулой межузлового напряжения, так как схема рис 3.10 представляет собой схему с двумя узлами,
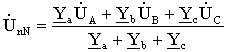
где: Ya = 1 / Za; Yb = 1 / Zb; Yc = 1 / Zc – комплексы проводимостей фаз нагрузки.
Очевидно, что теперь напряжения на фазах приемника будут отличаться друг от друга. Из второго закона Кирхгофа следует, что
Úa = ÚA - ÚnN; Úb = ÚB - ÚnN; Úc = ÚC - ÚnN.
Зная фазные напряжения приемника, можно определить фазные токи:
İa = Úa / Za = YaÚa; İb = Úb / Zb = YbÚb; İc = Úc / Zc = YcÚc.
Векторы фазных напряжений можно определить графически, построив векторную (топографическую) диаграмму фазных напряжений источника питания и UnN (
При изменении величины (или характера) фазных сопротивлений напряжение смещений нейтралиUnN может изменяться в широких пределах. При этом нейтральная точка приемника n на диаграмме может занимать разные положения, а фазные напряжения приемника Úa, Úb и Úc могут отличаться друг от друга весьма существенно.
Таким образом, при симметричной нагрузке нейтральный провод можно удалить и это не повлияет на фазные напряжения приемника. При несимметричной нагрузке и отсутствии нейтрального провода фазные напряжения нагрузки уже не связаны жестко с фазными напряжениями генератора, так как на нагрузку воздействуют только линейные напряжения генератора. Несимметричная нагрузка в таких условиях вызывает несимметрию ее фазных напряжений Úa, Úb, Úc и смещение ее нейтральной точки n из центра треугольника напряжений (смещение нейтрали).
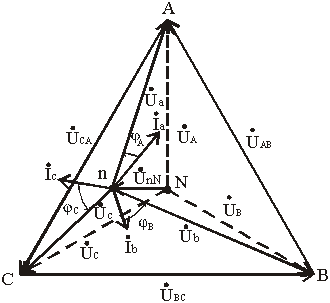
Направление смещения нейтрали зависит от последовательности фаз системы и характера нагрузки.
Поэтому нейтральный провод необходим для того, чтобы:
выравнивать фазные напряжения приемника при несимметричной нагрузке;
подключать к трехфазной цепи однофазные приемники с номинальным напряжением в раз меньше номинального линейного напряжения сети.
Следует иметь в виду, что в цепь нейтрального провода нельзя ставить предохранитель, так как перегорание предохранителя приведет к разрыву нейтрального провода и появлению значительных перенапряжений на фазах нагрузки.
Роль нейтрального провода
Нейтральный (нулевой рабочий) провод — провод, соединяющий между собой нейтрали электроустановок в трёхфазных электрических сетях.
При соединении обмоток генератора и приёмника электроэнергии по схеме «звезда» фазное напряжение зависит от подключаемой к каждой фазе нагрузки. В случае подключения, например, трехфазного двигателя, нагрузка будет симметричной, и напряжение между нейтральными точками генератора и двигателя будет равно нулю. Однако, в случае, если к каждой фазе подключается разная нагрузка, в системе возникнет так называемое напряжение смещения нейтрали, которое вызовет несимметрию напряжений нагрузки. На практике это может привести к тому, что часть потребителей будет иметь пониженное напряжение, а часть повышенное. Пониженное напряжение приводит к некорректной работе подключенных электроустановок, а повышенное может, кроме этого, привести к повреждению электрооборудования или возникновению пожара. Соединение нейтральных точек генератора и приёмника электроэнергии нейтральным проводом позволяет снизить напряжение смещения нейтрали практически до нуля и выровнять фазные напряжения на приёмнике электроэнергии. Небольшое напряжение будет обусловлено только сопротивлением нулевого провода.
33-34
на рисунке показана несимметричная нагрузка R L C элементов схема звезда. То что пунктиром чертить не нужно. Чтобы начертить симметричную активную нагрузку соединение звезда нужно все токи направить вдоль каждой оси напряжения как Ia.
Пример построения векторных диаграмм (при соединении нагрузки по схеме «треугольник»)
В отношении любой фазы справедливы все формулы, полученные ранее для однофазных цепей, например
Iab = Uab /zab ; φab = arcsin xab /zab ; Рab = Uab Iab cos φab = Iab2rab
Qab = Uab Iab sin φab = Iab2xab ; Sab = Uab Iab = Iab2zab = √Pab2 + Qab2
Очевидно, при симметричной нагрузке
Iab = Ibc = Ica = Iф ;
φab = φbc = φca = φф ;
Pab = Pbc = Pca = Pф ;
Qab = Qbc = Qca = Qф ;
Sab = Sbc = Sca = Sф .
Векторная диаграмма фазных (линейных) напряжений, а также фазных токов при симметричной активно-индуктивной нагрузке приведена на рис. 3.13, а. Там же построены векторы линейных токов. Следует обратить внимание на то, что при изображении векторных диаграмм в случае соединения треугольником вектор линейного напряжения Uabпринято направлять вертикально вверх.
Из приведенных выражений и векторной диаграммы следует, что при симметричной нагрузке существуют симметричные системы фазных и линейных токов.
Ia =2Iab sin60°=√3Iab,
Такое же соотношение существует между любыми другими фазными и линейными токами. Поэтому можно написать, что при симметричной нагрузке вообще
Ia =√3Iф .
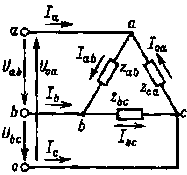
Рис. 3.12. Соединение фаз приемника треугольником
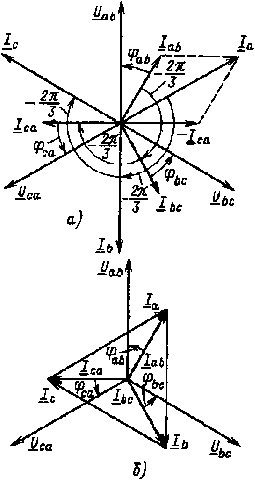
Рис. 3.13. Векторные диаграммы при соединении приемника треугольником в случае симметричной нагрузки
Мощность трехфазных цепей
Активная и реактивная мощности трехфазной цепи, как для любой сложной цепи, равны суммам соответствующих мощностей отдельных фаз:
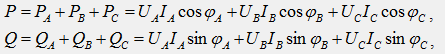
где IA, UA, IB, UB, IC, UC – фазные значения токов и напряжений.
В симметричном режиме мощности отдельных фаз равны, а мощность всей цепи может быть получена путем умножения фазных мощностей на число фаз:
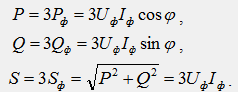
В полученных выражениях заменим фазные величины на линейные. Для схемы звезды верны соотношения Uф/Uл/√3, Iф=Iл, тогда получим:
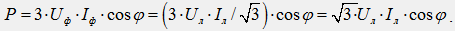
Для схемы треугольника верны соотношения: Uф=Uл ; Iф=Iл / √3 , тогда получим:
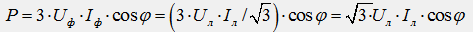
Следовательно, независимо от схемы соединения (звезда или треугольник) для симметричной трехфазной цепи формулы для мощностей имеют одинаковый вид:
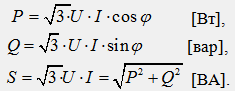
В приведенных формулах для мощностей трехфазной цепи подразумеваются линейные значения величин U и I, но индексы при их обозначениях не ставятся.
Узел, контур, ветвь, схема замещения
Ветвью называется один или несколько соединенных последовательно элементов заключенных между двумя узлами в которых протекает один ток. Ветви соединенные между двумя узлами образуют парал-е соединение.
Узел – место соединения трех или большего числа ветвей
Контур – замкнутая часть цепи проходящая по нескольким ветвям. Контуры, которые отл-ся хотя бы одной ветвью называются независимыми.
За положительное направление токов принято считать движение положительных зарядов поэтому ток пассивных элементов протекает от точки с большим потенциалом к точке с меньшим, в активных - наоборот, что соответствует определению ЭДС, как величины, характерезующей способность стороннего поля вызывать эл. ток во внешней цепи заданного направления.
3.а) Закон Омаустанавливает связь между напряжением тока и сопротивлением.
I =U /R для пасивного элемента
Для участка цепи пасивного элемента положительной направление тока, например, от т.1до т.2, т.е. от большего потенциала к меньшему напряжение будет равно:
U1,2=-E1+IR
I= (U1,2 +- E1)/R
Знак перед ЭДС определяется взаимным направлением тока и ЭДС.При совпадении направлений, ЭДС берут «+», в противном случае – «–»
б) Закон Ома замкнутой цепи с источником ЭДС

I = E/(Ru+Rл+Rн)
E = IRu+IRл+IRн
IRu – падение напряжения на источнике
IRл – падение напряжения внутри линии
IRн – падение напряжения нагрузки
в) Внешняя характеристика
Uu=E- ∆Uн

W=I2Rt; W-кол-во преобразующ. Энергии
P=I2R=U2/R=UI
законДжоуля-ЛенсаQ=A=I2Rt
Баланс активной мощности
Активная мощность, развиваемая источником равна сумме мощностей потребляемых всеми приемниками
EI=I2Ru+I2Rл+I2Rн
∆Ru-мощность, расходующаяся на нагрев ание источника
∆Rл – мощность, на нагревание линии передач
∆Rн – мощность, потребляемая нагрузкой
Pэ= ∆Pu+∆Pл+∆Рн
Законы Кирхгофа.
Соотношение между токами ЭДС в ветвях эл. цепи и напряжением на элементах определяется 2-мя законами Кирхгофа.
1 закон. Устанавливает законбаланса тока в разветвленной эл. цепи.
Алгебраическая сумма токов сходящихся в узле равно 0.
∑I=0 I1+I2+I3+I4=0
Либо сумма входящих равнасумме исходящих. I1+I2+I3=I4
2 Закон. Алгебраическая сумма ЭДС в контуре равна алгебраической сумме падений напряжений наэлементах этого контура.
∑E=∑U=∑IR
 Выбираем направление отхода контура по часовой стрелки.
Выбираем направление отхода контура по часовой стрелки.
ЭДС совпадающая с направлениес отхода контура – «+», в противном случае – «–»
E1-E2- I1R1+ I2R2 + I3R3 -I4R4=0
В графич. виде подтверждение закона Кирхгофа яыляется диаграмма.
Зависимость потенциалов контура от сопротивлений.


5. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла.
При последовательном соединении проводников сила тока в любых частях цепи одна и та же: I= I1=I2
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: U= U1+U2+ U3+U4
А сопротивление R= R1+R2+R3+R4
U= U1+U2+ U3+U4= I1R1+ I1R2+ I1R3+ I1R4=I1(R1+R2+R3+R4) = I1Rэкв .
P= I2Rэкв
При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединённых проводниках: I= I1+I2
Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же:
U= U1=U2
Сопротивление 1/R= 1/R1+1/R2+1/R3…..
g=1/R
