Методы расчета механического поведения сплавов с учетом их реологических свойств

ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению контрольных работ по дисциплине

«ТЕОРИЯ ЛИТЕЙНЫХ ПРОЦЕССОВ»

для студентов заочной формы обучения

направления подготовки 051000.62 Профессиональное обучение (по отраслям) профиля подготовки «Металлургия» профилизации «Технология и менеджмент в металлургических производствах»

Екатеринбург

2013

Задания и методические указания к выполнению контрольных работ по дисциплине «Теория литейных процессов». Екатеринбург, ФГАОУ ВПО «Российский государственный профессионально-педагогический университет», 2013. 66 с.

Автор:	канд. тех. наук., доц.	Ю.И. Категоренко

Одобрены на заседании кафедры автоматизации технологии литейных процессов. Протокол от «24»января2013г. № 5.

Заведующий кафедрой автоматизации технологии литейных процессов

Ю.И. Категоренко

Рекомендованы к печати методической комиссией Машиностроительного института РГППУ. Протокол от 13 февраля 2013. № 6.

Председатель методической комиссии МаИ		А.В. Песков

© Российский государственный

профессионально-педагогический

университет, 2013

© Категоренко Ю.И., 2013

Введение

Теория литейных процессов – фундаментальная техническая наука, занимающаяся изучением закономерностей процессов, происходящих при формировании отливок. Это относительно молодая наука, ее возраст не превышает 70–80 лет. Термин «теория литейных процессов» был предложен профессором Б.Б. Гуляевым в конце 50-х гг. прошлого века.

Литейные процессы отличаются большим многообразием. К ним относят механические процессы, процессы тепломассообмена при охлаждении и затвердевании сплавов, процессы кристаллизации в больших объемах и формирования кристаллической структуры отливок, усадочные явления, обусловливающие возникновение объемных дефектов и напряженного состояния сплава в отливках, гидродинамические процессы, происходящие при заполнении формы сплавом и компенсации объемной усадки при затвердевании отливок, процессы растворения и удаления газов из расплавов и т. п.

Особенностью литейных процессов является то, что указанные явления протекают практически одновременно. Это обусловливает большую сложность литейных процессов и трудности при их количественном описании. Литейные процессы являются многофакторными, поэтому в описывающих их уравнениях содержится много переменных, которые влияют на развитие процессов в разных направлениях. Важнейшая задача количественной теории литейных процессов – определение путей оптимального управления технологией и расчет соответствующих оптимальных значений технологических параметров процессов.

Дисциплина «Теория литейных процессов» решает следующие взаимосвязанные задачи: формирование у студентов фундаментальной базы знаний о процессах, происходящих при затвердевании отливок, и развитие навыков и умений решения различных задач по анализу литейных процессов и определению условий их оптимальной организации.

В прил. 1 содержатся необходимые справочные данные для решения задач. Задачи представлены в виде многовариантных заданий. Это позволяет использовать учебно-методическое пособие на практических занятиях, в процессе самостоятельной работы студентов, а также при выполнении домашних контрольных заданий.

Тело Максвелла (М-тело)

Рис. 1.6. Схема тела Максвелла (а) и изменение его деформации при σ = const (б)

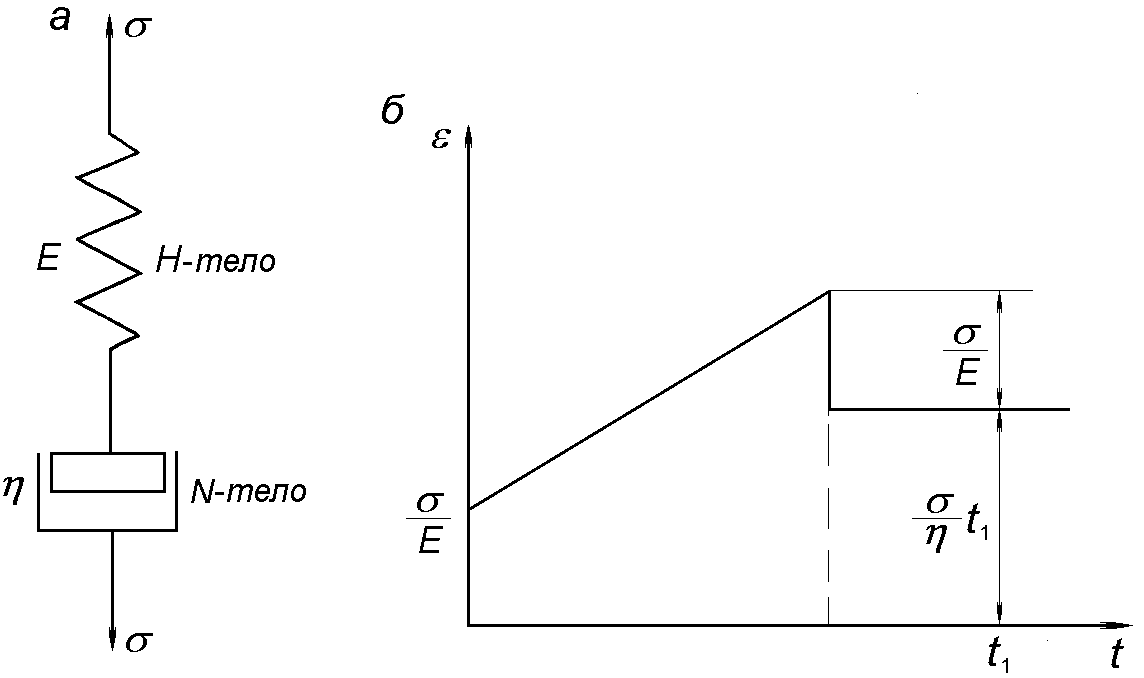
Тело Максвелла представляет собой последовательно соединенные тела Гука и Ньютона (рис. 1.6, а).

Деформация тела Максвелла равна сумме деформаций тела Гука (ε₁) и тела Ньютона (ε₂), т.е. .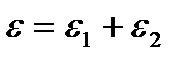

; ; ;

; .

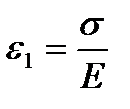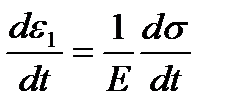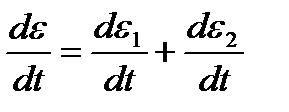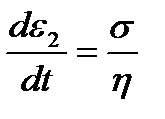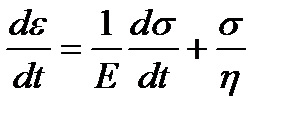Основное реологическое уравнение тела Максвелла можно записать следующим образом:

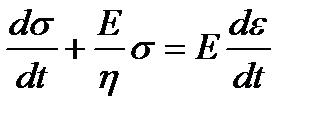. (1.9)

Решим уравнение (1.9) для двух частных случаев: σ=const и ε=const.

При постоянном напряжении (σ=const) 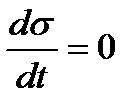и (1.9) принимает вид 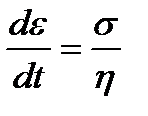. Отсюда .

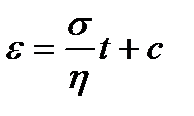При t=0 тело Гука мгновенно деформируется на величину 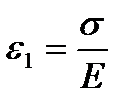, а деформация тела Ньютона при t=0 ε₂=0. С учетом этого находим 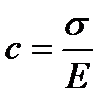и 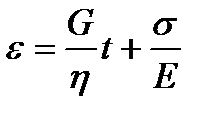. При t=t₁ 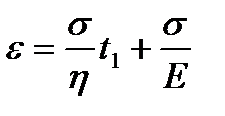. Если в момент t=t₁ разгрузить тело, т.е. выполнить следующее условие: при t>t₁ σ=0, то упругая деформация 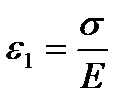исчезнет и останется остаточная деформация .

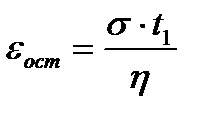При постоянной деформации, т.е. при ε=ε₀=const, уравнение (1.9) принимает вид

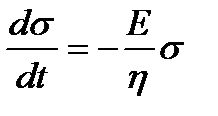, или .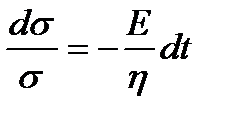

Интегрируя это уравнение, получаем

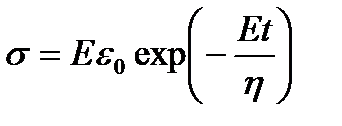. (1.10)

Из (1.10) видно, что напряжение монотонно убывает со временем, стремясь к нулю при .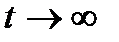

Процесс уменьшения напряжения при ε=const называется релаксацией напряжений. Уменьшение напряжений вызывается переходом упругой деформации тела Гука в пластическую деформацию тела Ньютона. При этом происходит постепенная разгрузка тела Гука.

Время 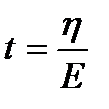называется временем релаксации. За время, равное времени релаксации, напряжение уменьшается в ε раз.

По механическому поведению к телу Максвелла близки сплавы в нижней, примыкающей к температуре солидуса, части интервала кристаллизации.

Тело Кельвина (К-тело)

Рис. 1.7. Схема тела Кельвина (а) и зависимость его деформации от времени при σ=const (б)

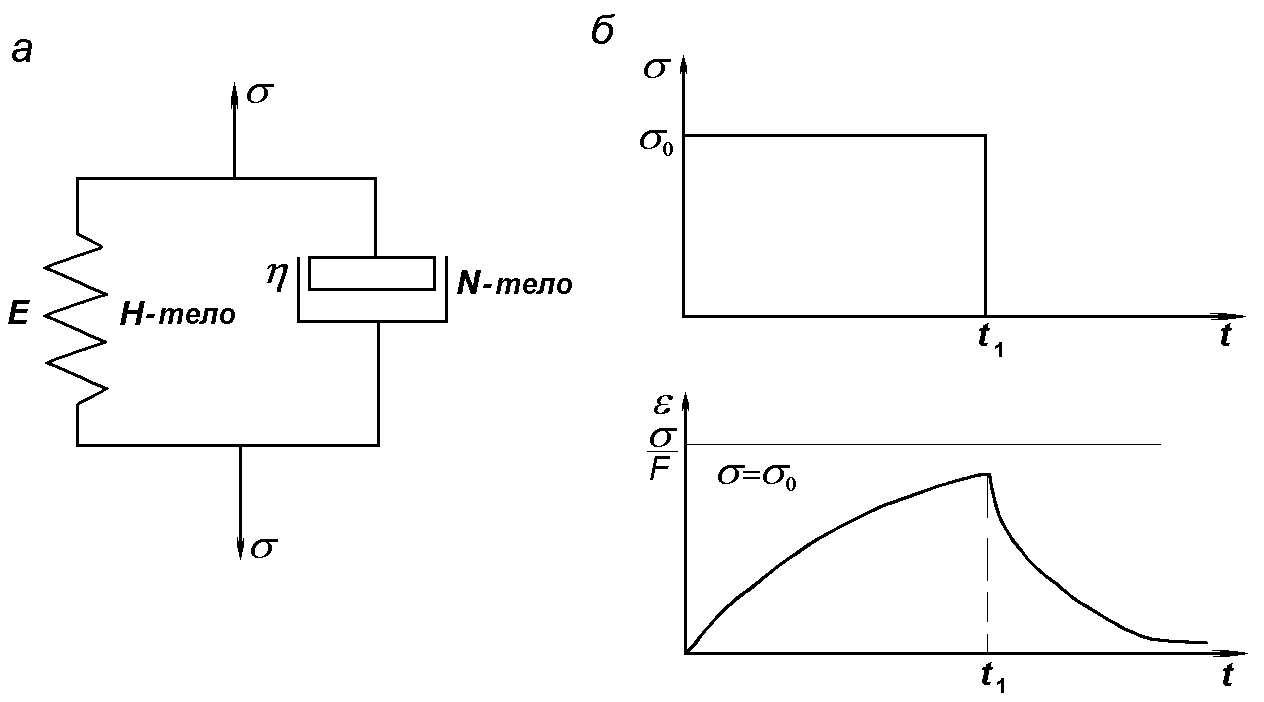
Тело Кельвина представляет собой систему параллельно соединенных тел Ньютона и Гука (рис. 1.7). Напряжение σ равно сумме напряжений в теле Ньютона – σ₁ и в теле Гука – σ₂: 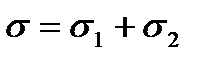; 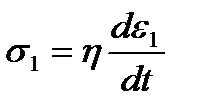и 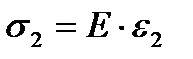.Так как элементы соединены параллельно, то их деформации равны, т.е. 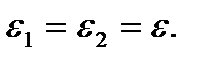С учетом этих выражений получаем дифференциальное реологическое уравнение тела Кельвина.

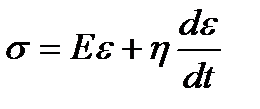, или 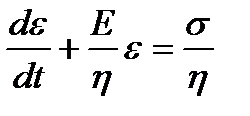. (1.11)

При σ=const уравнение (1.11) – линейное дифференциальное уравнение первого порядка с постоянной правой частью.

Примем , .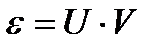

; ; ;

; ; .

; ;

.

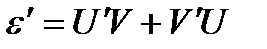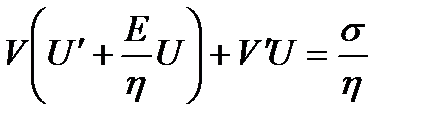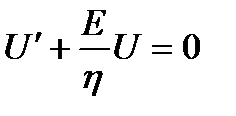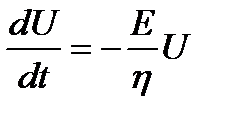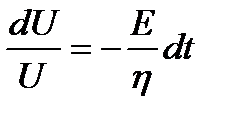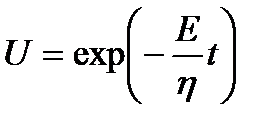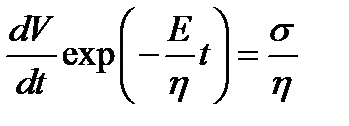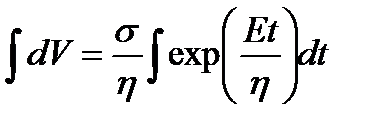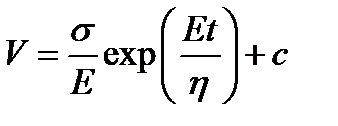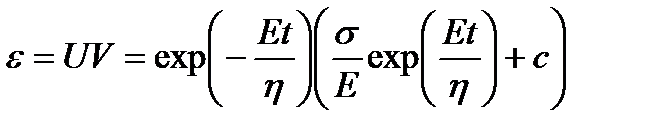Мгновенное приложение нагрузки при t=0 не может вызвать соответствующую деформацию тела Гука, так как параллельно соединенное с ним тело Ньютона не дает ему мгновенно деформироваться. Поэтому ε=0 при t=0. С учетом этого имеем 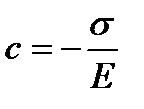. Тогда

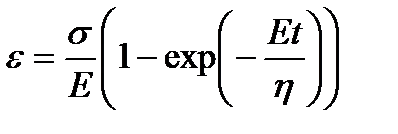. (1.12)

Из (1.12) видно, что с ростом времени ε монотонно растет, стремясь к 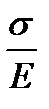при t 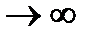. Если при t=t₁ снять нагрузку, то деформация будет монотонно уменьшаться, стремясь к нулю.

Так как мгновенная деформация тела Кельвина невозможна, решение по (1.11) при 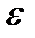=const не проводится.

Тело Бингама (В-тело)

Тело Бингама представляет собой совокупность параллельно соединенных тел Сен-Венана и Ньютона (рис. 1.8).

Рис. 1.8. Схема тела Бингама (а) и изменение деформации тела Бингама (б) при τ = const

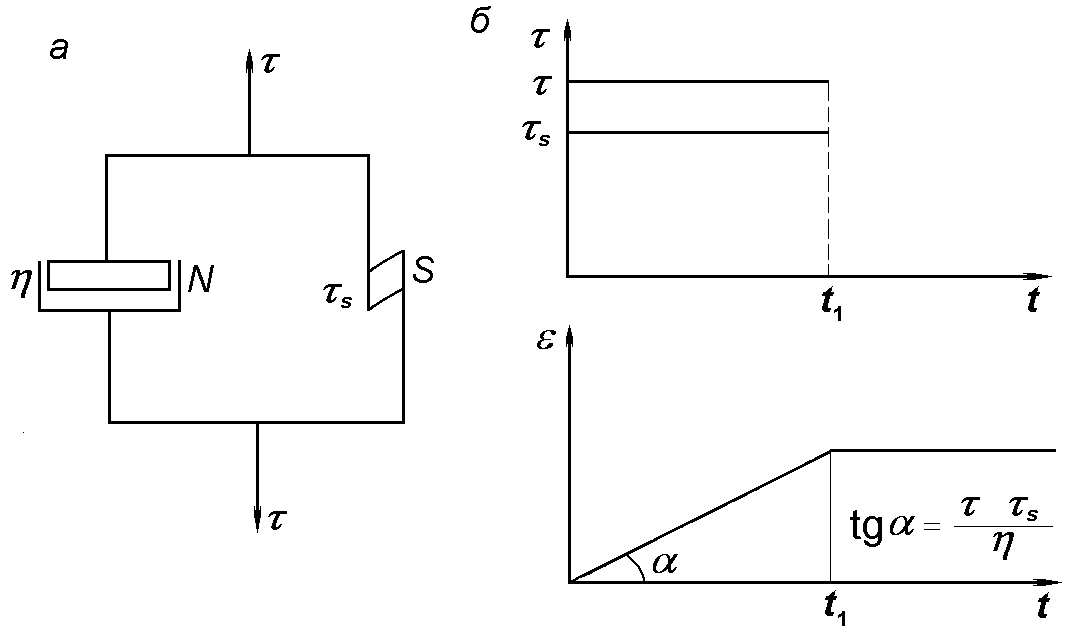
При τ<τ_s скорость деформации тела Сен-Венана равна нулю. Поэтому равна нулю и скорость деформации тела Ньютона, а также всего тела Бингама.

При τ 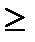τ_s напряжение тела Сен-Венана равно τ_s, а напряжение тела Ньютона – τ_N=τ–τ_s. Тогда реологический закон тела Бингама имеет вид

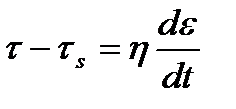^, или 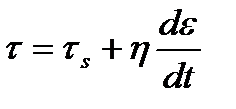. (1.13)

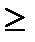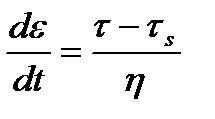При τ<τ_s ε=0. При τ τ_s , или 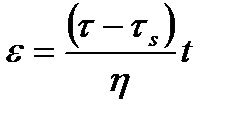. При t=t₁ в теле будет остаточная деформация .

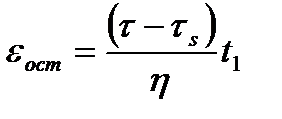По типу тела Бингама ведут себя вязкопластические жидкости, к которым относятся концентрированные суспензии. К этим же телам можно отнести сплавы внутри интервала кристаллизации вблизи температуры ликвидуса. В этом случае сплавы представляют собой суспензию, количество твердой фазы в которой для бинарных сплавов можно определить по правилу рычага. Величина предельного касательного напряжения τ_s и структурная вязкость η зависят от количества и формы выделений твердой фазы. При некотором количестве твердой фазы, соответствующем температуре нулевой жидкотекучести, напряжения, развиваемые активными силами, движущими поток сплава в форме, становятся меньше τ_s. При этом происходит остановка потока сплава.

Тело Шведова (Sch-тело)

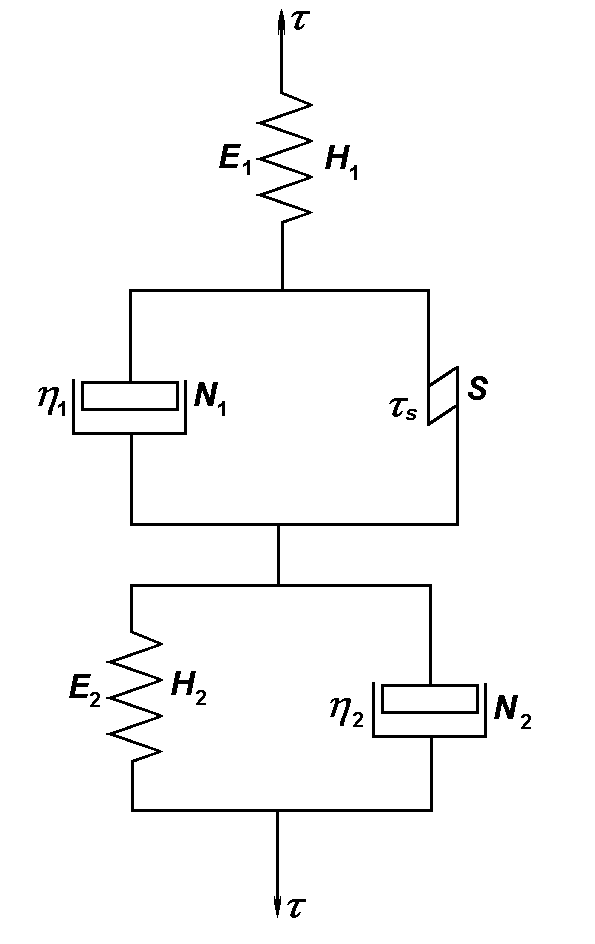
Рис. 1.9. Схема тела Шведова

В исследованиях Г.Ф. Баландина и Л.П. Каширцева показано, что реологическое поведение сплавов в широком интервале температур может быть описано моделью тела Шведова, представляющего собой комбинацию тел Гука, Бингама и Кельвина (рис. 1.9).

Поведение сплава описывается пятью реологическими характеристиками: E₁, E₂, η₁, η₂ и τ_s, которые изменяются в зависимости от температуры. Реологические свойства алюминиево-кремниевого сплава и основные зависимости реологической модели тела Шведова рассматриваются в п. 4.3 в в связи с анализом напряжений и деформаций в отливках.

Объемная и линейная усадка

Уменьшение объема при охлаждении сплава называют объемной усадкой, а уменьшение линейных размеров – линейной усадкой. Различают объемную усадку в жидком и твердом состояниях, а также при затвердевании.

Зависимость объема залитого в форму сплава от температуры выражается формулой

,

где V₀ – объем полости формы, см³;

α_Vж – коэффициент температурного расширения жидкого сплава, К^–1.

Коэффициент α_Vж зависит от природы и состава сплава. Пределы его изменения – от 0,2·10^–4 до 2 10^–4 К^–1.

Объемную усадку в жидком состоянии можно вычислить по формуле

.

Коэффициент объемной усадки в жидком состоянии равен

(2.1)

Относительная объемная усадка при затвердевании имеет порядок 2÷5 %, она вычисляется по формуле

.

При затвердевании сплавов происходит предусадочное расширение ε_Vp, которое в ряде случаев может частично или полностью скомпенсировать усадку при затвердевании. Например, при затвердевании серого чугуна выделяется графит, имеющий значительно меньшую плотность, чем жидкий сплав. Это приводит к расширению объема, компенсирующему объемную усадку.

Объемная усадка в твердом состоянии характеризуется коэффициентом ;

, (2.2),

где Т_к – температура в конце охлаждения отливки.

В железоуглеродистых сплавах относительная усадка в твердом состоянии равна

,

где ε_Vт.д.п – доперлитная усадка;

ε_Vт.п.п – послеперлитная усадка;

ε_Vγ→α – расширение при эвтектическом превращении.

Линейная усадка, характеризующая уменьшение размеров отливки, начинается при температуре Т_y внутри интервала ликвидус–солидус, при которой сплав теряет свою подвижность как единое целое. Линейная относительная усадка вычисляется по формуле

.

Коэффициент линейной усадки α_л зависит от температуры, однако в расчетах применяют некоторое усредненное значение, имеющее порядок 10^-6. Для усадки в твердом состоянии справедлива зависимость α_Vт=3α_л.

Относительная линейная усадка стержней составляет от 2 до 3%, для серого чугуна ε_л=0,6–0,9%, для белого чугуна ε_л=1,5–1,7%. У алюминиевых сплавов ε_л находится в пределах от 0,8 до 1,5%.

Суммарная относительная объемная усадка равна

, (2.3)

где V_к – объем сплава при конечной температуре.

Суммарная относительная объемная усадка представляет собой алгебраическую сумму усадки в жидком состоянии, при затвердевании, пред-усадочного расширения и усадки в твердом состоянии

. (2.4)

Эту величину можно выразить формулой

,

где ρ_ж и ρ_т – плотность сплава в жидком и твердом состояниях.

Величина называется относительной линейной усадкой. , где ε_тех – относительная усадка, вызванная изменениями размеров полости формы вследствие расталкивания модели перед извлечением ее из формы, а также в процессе сушки и отделки формы.

Рассмотренная выше величина ε_л характеризует свободную, незатрудненную усадку и является физической характеристикой сплава. Однако в реальных условиях чаще всего мы имеем дело с затрудненной усадкой. Вследствие препятствий со стороны стержней и выступающих частей формы усадка реализуется не в полной мере. Кроме указанного механического торможения усадки имеет место термическое торможение усадки, вызванное неравномерным охлаждением отдельных частей отливки. Торможение усадки приводит к возникновению в отливке литейных напряжений. Отношение называется степенью торможения усадки.

Список рекомендуемой литературы

Основная

1. Чуркин Б.С. и др. Специальные способы литья Учеб./ Екатеринбург: Изд-во Рос.гос.проф.-пед.ун-та, 2010.-730с.

2. Д. М. Кукуй, В. А. Скворцов, Н. В. Андрианов Теория и технология литейного производства. В 2 частях. – М.: Новое знание, 2011.–– 800 с.

Дополнительная

1. Чуркин Б.С. Теория литейныхпроцессов. Екатеринбург: Рос. гос. проф.-пед. ун-т, 2006. 453 с.

2. Теория литейных процессов/Б.С.Чуркин, Э.Б.Гофман, А.Б.Чуркин, Ю.И. Категоренко. Екатеринбург, 2006. 196 с.

3. Баландин Г.Ф. Основы теории формирования отливок.- М.: Машиностроение, 1976,- 328 с.

4. Баландин Г.Ф. Основы теории формирования отливки: В 2 ч. 4.2, Формирование макроскопического строения отливки. - М: Машино­строение, 1979. - 335 с.

5. Баландин Г.Ф. Формирование кристаллического строения отливок.-М.: Машиностроение, 1973.- 286 с.

6. Баландин Г.Ф., Васильев В А. Физико-химические основы литейного производства. - М.: Машиностроение, 1971. - 244 с.

7. ГуляевВ.В. Теория литейных процессов- Л.: Машиностроение, 1976. -216 с.

8. Константинов ЛС, Труте АЛ. Напряжения, деформации и трещины в отливках,- М: Машиностроение, 1981. -194 с.

9. Куманин И.В. Вопросы теории литейных процессов. - М.: Машиностроение, 1976.- 216 с.

10. Рабинович Б.В. Введение в литейную гидравлику. - М.: Машиностроение, 1967-272 с.

11. Чуркин Б.С, Теоретические основы литейных процессов: Учеб. пособие/Свердд.инж.-пед.ин-г- Свердловск, 1991. - 200 с.

12. Чуркин Б. С. Численные методы расчета кинетики затвердевания отливок/ Урал, политехи, ин-т. - Свердловск. 1986. - 62с.

Основные обозначения

с₁, с₂, с_т.ж – удельная теплоемкость сплавов в твердом, жидком и твердо-жидком состояниях, Дж/(г·К)

ρ₁, ρ₂, ρ_ж.т – плотность сплавов в твердом, жидком и жидко-твердом состояниях, г/см³

b₁ – коэффициент аккумуляции тепла сплавом, Вт·с/(см²·К)

b_ф – коэффициент аккумуляции тепла материалом формы, Вт·с/(см²·К)

с_ф и ρ_ф – удельная теплоемкость, Дж/(г·К), и плотность, г/см³, материала формы

λ₁, λ₂, λ_ж.т – теплопроводность сплава в твердом, жидком и жидко-твердом состояниях, Вт/(м·К)

Q_кр – удельная теплота кристаллизации сплава, выделяющаяся в интервале ликвидус–солидус, Дж/г

Q_кр.сол – удельная теплота кристаллизации сплава, выделяющаяся при эвтектическом превращении, Дж/г

Т_л, Т_с – температуры ликвидуса и солидуса сплава, ^оС

Т_н.ж – температура нулевой жидкотекучести сплава, ^оС

Т_А – температура плавления основы сплава, ^оС

Ψ – доля твердой фазы

L – удельная теплота кристаллизации сплава, Дж/г

n – скорость возникновения центров кристаллизации, см^–3·с^–1

ΔТ₁ – интервал метастабильности сплава, ^оС

τ_s – предельное касательное напряжение сплава, МПа

D – коэффициент диффузии, см²/с

t_max – максимальная продолжительность заливки формы, с

μ – динамический коэффициент вязкости перегретого сплава, МПа·с

υ – кинематический коэффициент вязкости, см²/с

К₀ – коэффициент распределения компонента в сплаве

D_г – гидравлический диаметр, мм

a – коэффициент температуропроводности, м/с²

Ra = Gr·Pr – критерий Рэлея

Re = v·D_г/υ – критерий Рейнольдса

Pe = v·D_г/a – критерий Пекле

Pr = υ/a – критерий Прандтля

Nu = α·D_г/λ – критерий Нуссельта

α – коэффициент теплопередачи, Вт/(см²·К)

Gr = gβL³ΔT/υ² – критерий Грасгофа

Bi = α·R/λ – критерий Био

d_з – средний размер зерна в структуре сплава, см

N_з – число зерен в единице объема затвердевшего сплава

σ_к.ж – межфазное натяжение на границе жидкого сплава и кристалла, мДж/м²

Q – расход сплава, см³/с

v – средняя скорость сплава, см/с

p₀ – давление на расплав, МПа

p_кр – критическое давление, МПа

ε_VΣ – суммарный коэффициент усадки в жидком состоянии, %

ε – линейная усадка, %

ПРИЛОЖЕНИЕ 1

ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению контрольных работ по дисциплине

«ТЕОРИЯ ЛИТЕЙНЫХ ПРОЦЕССОВ»

Подписано в печать 2013. Форат 60×84/16. Бумага для множ. аппаратов. Печать плоская. Усл.-печ. л. . Уч.-изд. л. . Тираж экз.

Заказ №

ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению контрольных работ по дисциплине

«ТЕОРИЯ ЛИТЕЙНЫХ ПРОЦЕССОВ»

для студентов заочной формы обучения

направления подготовки 051000.62 Профессиональное обучение (по отраслям) профиля подготовки «Металлургия» профилизации «Технология и менеджмент в металлургических производствах»

Екатеринбург

2013

Задания и методические указания к выполнению контрольных работ по дисциплине «Теория литейных процессов». Екатеринбург, ФГАОУ ВПО «Российский государственный профессионально-педагогический университет», 2013. 66 с.

Автор:	канд. тех. наук., доц.	Ю.И. Категоренко

Одобрены на заседании кафедры автоматизации технологии литейных процессов. Протокол от «24»января2013г. № 5.

Заведующий кафедрой автоматизации технологии литейных процессов

Ю.И. Категоренко

Рекомендованы к печати методической комиссией Машиностроительного института РГППУ. Протокол от 13 февраля 2013. № 6.

Председатель методической комиссии МаИ		А.В. Песков

© Российский государственный

профессионально-педагогический

университет, 2013

© Категоренко Ю.И., 2013

Введение

Теория литейных процессов – фундаментальная техническая наука, занимающаяся изучением закономерностей процессов, происходящих при формировании отливок. Это относительно молодая наука, ее возраст не превышает 70–80 лет. Термин «теория литейных процессов» был предложен профессором Б.Б. Гуляевым в конце 50-х гг. прошлого века.

Литейные процессы отличаются большим многообразием. К ним относят механические процессы, процессы тепломассообмена при охлаждении и затвердевании сплавов, процессы кристаллизации в больших объемах и формирования кристаллической структуры отливок, усадочные явления, обусловливающие возникновение объемных дефектов и напряженного состояния сплава в отливках, гидродинамические процессы, происходящие при заполнении формы сплавом и компенсации объемной усадки при затвердевании отливок, процессы растворения и удаления газов из расплавов и т. п.

Особенностью литейных процессов является то, что указанные явления протекают практически одновременно. Это обусловливает большую сложность литейных процессов и трудности при их количественном описании. Литейные процессы являются многофакторными, поэтому в описывающих их уравнениях содержится много переменных, которые влияют на развитие процессов в разных направлениях. Важнейшая задача количественной теории литейных процессов – определение путей оптимального управления технологией и расчет соответствующих оптимальных значений технологических параметров процессов.

Дисциплина «Теория литейных процессов» решает следующие взаимосвязанные задачи: формирование у студентов фундаментальной базы знаний о процессах, происходящих при затвердевании отливок, и развитие навыков и умений решения различных задач по анализу литейных процессов и определению условий их оптимальной организации.

В прил. 1 содержатся необходимые справочные данные для решения задач. Задачи представлены в виде многовариантных заданий. Это позволяет использовать учебно-методическое пособие на практических занятиях, в процессе самостоятельной работы студентов, а также при выполнении домашних контрольных заданий.

МЕТОДЫ РАСЧЕТА МЕХАНИЧЕСКОГО ПОВЕДЕНИЯ СПЛАВОВ С УЧЕТОМ ИХ РЕОЛОГИЧЕСКИХ СВОЙСТВ

В процессе формирования отливки температура сплава изменяется в широких пределах: от температуры заливки до температуры цеха. При этом меняется состояние сплава и его физико-механические свойства. При температуре заливки жидкий сплав представляет собой ньютоновскую жидкость, кинематическая вязкость которой близка к кинематической вязкости воды. В верхней части интервала кристаллизации сплав является суспензией, сохраняющей текучесть, но не подчиняющейся ньютоновскому закону вязкого трения. При некоторой температуре происходит структурирование расплава и он начинает проявлять свойства твердого тела. Изменяются в широких пределах не только физико-механические свойства сплава, но и его природа. Для эффективной организации технологического процесса получения отливки необходимо знать, как изменяются реологические свойства сплава.

Реология – наука, изучающая развитие напряжений и деформаций в телах различной природы. Основой для исследования механического поведения тел является их реологическое уравнение, связывающее между собой напряжения (σ – нормальное напряжение или τ – касательное напряжение), деформации (ε, γ), скорости деформации ( , ), скорости изменения напряжений ( , ) и т. п.:

; (1.1)

. (1.2)

Как известно из курса сопротивления материалов, под действием приложенных к телу усилий в нем развивается сложное напряженное состояние, характеризующееся тензорами напряжений и деформаций. Действующее в данной точке напряжение относительно выбранной площадки можно разложить на две составляющие: нормальную σ_n и касательную τ (рис. 1.1). В дальнейшем нормальную составляющую будем обозначать просто буквой σ.

Рис. 1.1. Разложение напряжения σ на нормальную (σn) и касательную (τ) составляющие