Повторные независимые испытания. Асимптотические формулы теории вероятностей
Число: 2085
- Формулы для расчета вероятности P (A) наступления события хотя бы один раз в серии из n испытаний с вероятностью наступления P(Ai) = р в каждом из них:
- P (A) = P (A1)+P (A2)+…+P (An)
- P (A) = 1 – (1 – p) n (*)
- P (A) = 1 – (P (
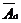 )P (
)P ( 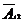 )…P (
)…P ( 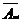 )) (*)
)) (*) - P (A) = 1 – (P (A1)P (A2)…P (An))
- P (A) = 1 – p n
- В цехе установлено 10 станков, надежность каждого из которых (вероятность работы в определенный промежуток времени) в течение смены равна 0.7. Найдите вероятность того, что в течение смены откажут не более 8 станков
- 0.64.
- *0.998.
- 1
- 0.5
- Определите вероятность того, что взятая наудачу деталь окажется высшего качества, если известно, что 4% всей продукции является браком, а 3/4 всех не бракованных изделий является продукцией высшего качества
- 0.8
- *0,72
- 3/8.
- ½
- 0,33
- Формула Пуассона используется при достаточно большом n, так что n*p
- меньше или равно 1
- *меньше или равно 10
- больше или равно 10
- больше или равно 1
- При достаточно большом n и р близком к 0,5 вероятность того, что в n независимых испытаниях событие А наступит m раз определяется по формуле
- Пуассона
- Бернули
- *Муавра-Лапласа
- полной вероятности
- Формула Пуассона
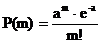 , где a=np, дает наиболее точное значение вероятности
, где a=np, дает наиболее точное значение вероятности
- при значениях p, близких к 1
- *при значениях p, близких к 0
- при любом значении p
- Утверждение о том, что число, формула Пуассона
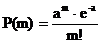 , где a=np, дает наиболее точное значение вероятности при значениях p, близких к 0,5, является
, где a=np, дает наиболее точное значение вероятности при значениях p, близких к 0,5, является
- Истинным
- *Ложным
- Верным только для совместных событий
- Утверждение о том, что число, формула Пуассона
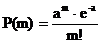 , где a=np, дает наиболее точное значение вероятности при значениях p, близких к 1, является
, где a=np, дает наиболее точное значение вероятности при значениях p, близких к 1, является
- Истинным
- *Ложным
- Верным только для совместных событий
- Утверждение о том, что число, формула Пуассона
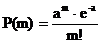 , где a=np, дает наиболее точное значение вероятности при значениях p, близких к нулю, является
, где a=np, дает наиболее точное значение вероятности при значениях p, близких к нулю, является
- *Истинным
- Ложным
- Верным только для совместных событий
- Точную вероятность появления события m раз в серии из n испытаний дает формула
- Пуассона
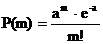
- *Бернулли Pn(m)=
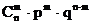
- Муавра-Лапласа Pn(m)=
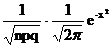
- P(m)=qm-1·p
- Вероятность рождения мальчика равна 0,51. Тогда вероятность того, что среди 100 новорожденных окажется 50 мальчиков можно вычислить по формуле
- P=(1–0,51)50·0,51
- *P=
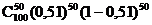
- P=
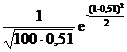
- P=
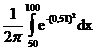
- Формула Пуассона для вычисления вероятности того, что в n независимых испытаниях событие А произойдет m раз, имеет вид
- *
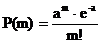
- Pn(m)=
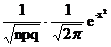
- Pn(m)=
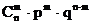
- Pn(m)=qm-1·p
- Вероятность того, что в серии из n независимых испытаний событие А произойдет m раз, если известно, что вероятность p события А в каждом испытании мала, а число испытаний n велико, лучше определять по формуле
- Бернулли;
- сложения вероятностей;
- *Пуассона;
- Муавра-Лапласа.
- Монета брошена 2N раз (N велико). Вероятность того, что “герб” выпадет N раз, предпочтительнее вычислять с использование
- *локальной теоремы Муавра-Лапласа
- формулы Бернулли
- формулы Пуассона
- формулы сложения вероятностей.
- При проведении контроля качества среди 1000 случайно отобранных деталей 5 оказалось бракованными. Среди 25000 деталей бракованных окажется:
- 535
- 250
- * 125
- 50
- При проведении контроля качества среди 1000 случайно отобранных деталей 5 оказалось бракованными. Среди 50000 деталей бракованных окажется:
- 535
- * 250
- 125
- 50
- Число m0 наступления события в серии из n испытаний называется наивероятнейшим числом, если
- это число является наибольшим среди всех остальных;
- оно совпадает с числом испытаний n;
- *оно соответствует наибольшей вероятности в данной серии испытаний;
- событие, соответствующее этому числу, достоверно.
- Наивероятнейшее число наступления события m0 находится в интервале
-
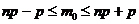
- *
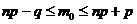
-
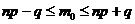
-
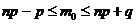
- Вероятность попадания стрелком в цель равна 0,7. Сделано 10 выстрелов. Наивероятнейшее число попаданий в цель:
- *7
- 15
- 18
- 20
- 25
- Вероятность попадания стрелком в цель равна 0,7. Сделано 15 выстрелов. Наивероятнейшее число попадания в цель:
- *11
- 14
- 18
- 20
- 25
- Вероятность попадания стрелком в цель равна 0,8. Сделано 10 выстрелов. Наивероятнейшее число попаданий в цель:
- *8
- 10
- 15
- 20
- 25
- Произведение меньшей, чем ½, вероятности появления события в одном испытании и числа произведенных испытаний в схеме Бернулли равно 127,45. Наивероятнейшее число появления события равно
- 127 (*)
- 128
- 126
- 128,45
- 127,95
- Вероятность того, что в небольшом числе n независимых испытаний с постоянной вероятностью р появления события в каждом из них событие А наступит m раз определяется по формуле
- полной вероятности
- Бернулли (*)
- нормального закона распределения
- Пуассона
- Байеса
- При большом числе независимых испытаний и постоянной, близкой к 0,5 вероятности р появления события в каждом из них вероятность наступления события m раз определяется по формуле
- Байеса
- Бернулли
- нормального закона распределения (*)
- полной вероятности
- Пуассона
- Наиболее вероятное число горожан, родившихся 29 февраля, при населении города 150 тыс. жителей:
- * 103
- 150
- 125
- 250
