Повторение школьной алгебры: «Решение рациональных
Уравнений и неравенств»
ЦЕЛЬ РАБОТЫ:
1. Повторить знания уч-ся в теме: «Решение рациональных уравнений и неравенств».
2. Организовать деятельность уч-ся по переводу своих знаний от усвоения отдельных фактов и понятий к их обобщению в целостную систему знаний.
3. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: справочные пособия по алгебре, микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Выполнить обучающий тест и проверить свои результаты по таблице ответов.
УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ
ПРИМЕР 1. Решите неравенство 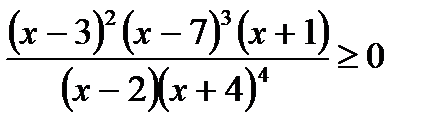 .
.
РЕШЕНИЕ. Это рациональное неравенство решим методом интервалов. Отметим на числовой прямой «жирными» точками нули числителя (–1; 3 и 7) и «прозрачными» – нули знаменателя (–4 и 2). Если бы заданное неравенство было строгим, нужно было бы все нули сделать «прозрачными». Эти точки разобьют числовую прямую на 6 интервалов:
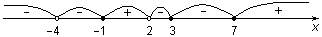
Выясним знак данной дроби на каждом из этих интервалов, используя пробные числа, принадлежащие интервалам.
Можно поступать иначе. Для этого в выражении в каждом из множителей переменная х должна иметь знак «+» ((х – 2), а не (2 – х); (х – 7), а не (7 – х)). Этого всегда можно добиться, умножая неравенство на –1 и меняя одновременно его знак столько раз, сколько надо. Отметив нули выражения на числовой оси, справа налево расставим знаки по следующему правилу: сначала «+», меняем знак на нечетной степени и сохраняем его на четной.
Теперь остается выписать ответ – промежутки, на которых поставлен знак «+», так как знак данного неравенства 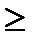 . Важно не забыть х = 3.
. Важно не забыть х = 3.
ОТВЕТ: 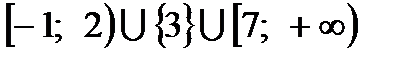 .
.
ПРИМЕР 2. Решите неравенство 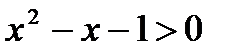 .
.
РЕШЕНИЕ. Это квадратное неравенство можно решить методом интервалов, но проще – графически. Рассмотрим функцию, заданную уравнением 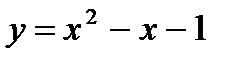 . Графиком ее является парабола. Заметим, что для нас совершенно не важны точные характеристики параболы (где находится ось, пересечение с Оу и т. п.) Достаточно знать, что ее ветви направлены вверх (а > 0) и что она пересекает осьОх в двух точках, являющихся корнями уравнения
. Графиком ее является парабола. Заметим, что для нас совершенно не важны точные характеристики параболы (где находится ось, пересечение с Оу и т. п.) Достаточно знать, что ее ветви направлены вверх (а > 0) и что она пересекает осьОх в двух точках, являющихся корнями уравнения 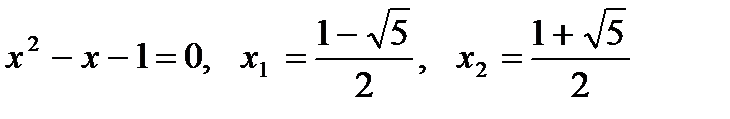 . Выполним схематический рисунок:
. Выполним схематический рисунок:
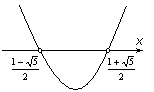
Из рисунка видно, что квадратичная функция принимает положительные значения вне отрезка, соединяющего ее корни.
ОТВЕТ: 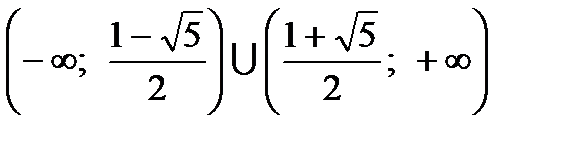 .
.
ЗАДАНИЯ ДЛЯ ПРАКТИЧЕСКОЙ РАБОТЫ
Вариант 1 1. Решите неравенства: а) 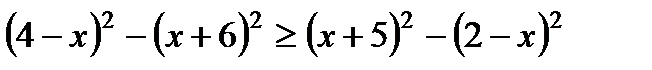 ; б) ; б) 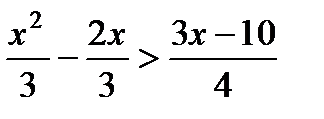 ; в) ; в) 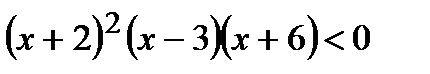 . 2. Решите систему неравенств: . 2. Решите систему неравенств: 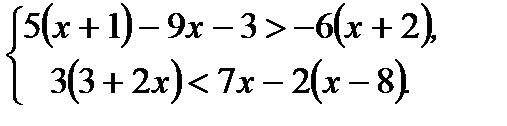 Вариант 3 1. Решите неравенства: а) Вариант 3 1. Решите неравенства: а) 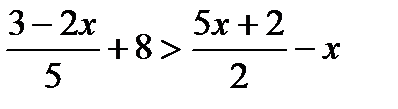 ; б) ; б) 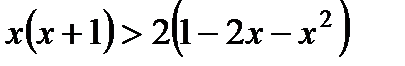 ; в) ; в) 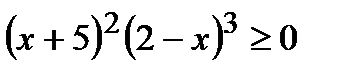 . 2. Решите систему неравенств: . 2. Решите систему неравенств: 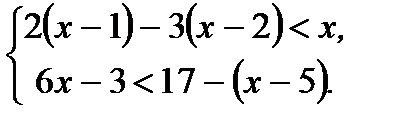 Вариант 5 1. Решите неравенства: а) Вариант 5 1. Решите неравенства: а) 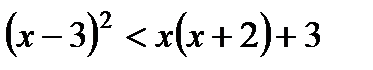 ; б) ; б) 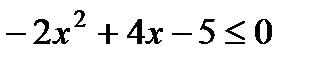 ; в) ; в) 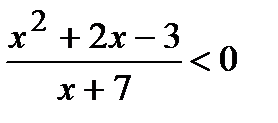 . 2. Решите систему неравенств: . 2. Решите систему неравенств: 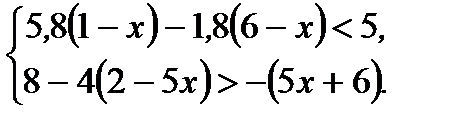 | Вариант 2 1. Решите неравенства: а) 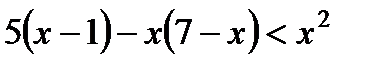 ; б) ; б) 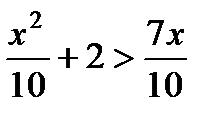 ; в) ; в) 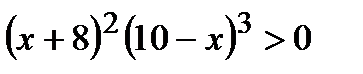 . 2. Решите систему неравенств: . 2. Решите систему неравенств: 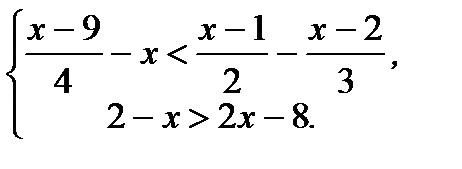 Вариант 4 1. Решите неравенства: а) Вариант 4 1. Решите неравенства: а) 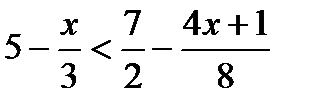 ; б) ; б) 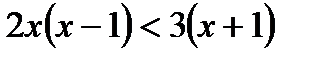 ; в) ; в) 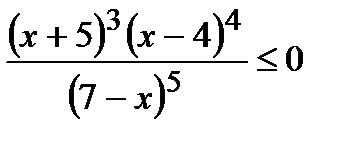 . 2. Решите систему неравенств: . 2. Решите систему неравенств: 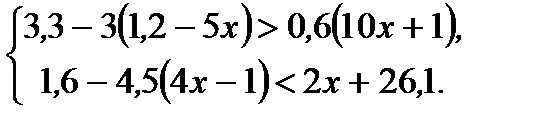 Вариант 6 1. Решите неравенства: а) Вариант 6 1. Решите неравенства: а) 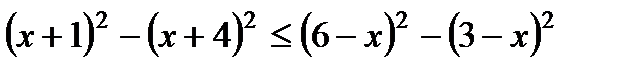 ; б) ; б) 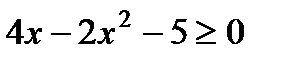 ; в) ; в) 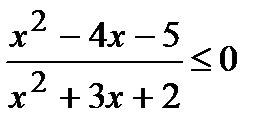 . 2. Решите систему неравенств: . 2. Решите систему неравенств: 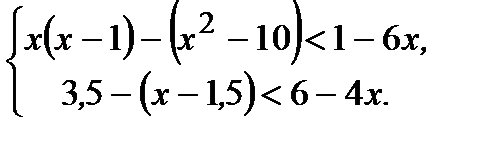 |
ТЕСТ 1. Квадратное уравнение и его корни.
1. Какое из уравнений является квадратным:
1) 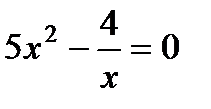 ; 3)
; 3) 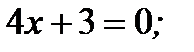
2) 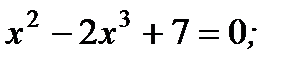 4)
4) 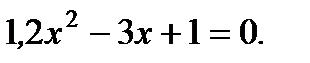
2. В квадратном уравнении 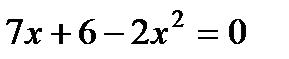 укажите его коэффициенты:
укажите его коэффициенты:
1) 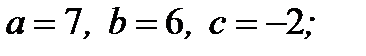 3)
3) 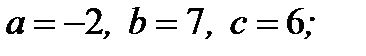
2) 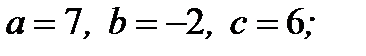 4)
4) 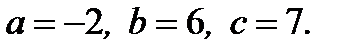
3. Определите, какое из приведённых уравнений является равносильным уравнению 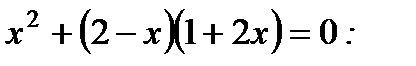
1) 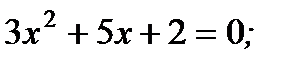 3)
3) 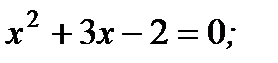
2) 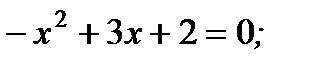 4)
4) 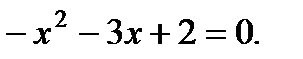
4. Найдите корни уравнения 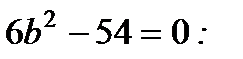
1) 0, 3; 2) –3, 3; 3) не имеет корней; 4) 3.
5. Какие из чисел - 4, - 2, - 1, 0, 2 являются корнями квадратного уравнения 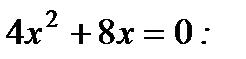
1) – 2, 0; 2) 0, 2; 3) – 4, - 1; 4) – 4, 0?
6. Решите уравнение 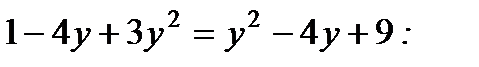
1) – 2, 0; 2) – 2, 2; 3) 2; 4) 0.
ТЕСТ 2. Формула корней квадратного уравнения.
1. Вычислите дискриминант квадратного уравнения 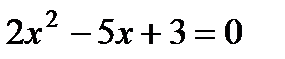 :
:
1) 49; 2) –1; 3) 1; 4) 25.
2. Определите, имеет ли квадратное уравнение 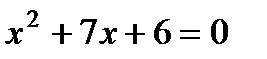 корни и если имеет, то сколько:
корни и если имеет, то сколько:
1) имеет один корень; 2) не имеет корней; 3) имеет два корня.
3. Найдите корни уравнения 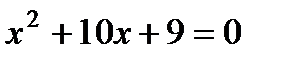 :
:
1) –1, –9; 2) –1, 9; 3) –9, 1; 4) 1, 9.
4. Решите квадратное уравнение 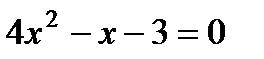 :
:
1) 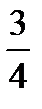 ,1; 2) –1,
,1; 2) –1, 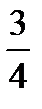 ; 3)
; 3) 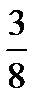 , 1; 4)
, 1; 4) 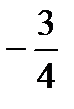 , 1.
, 1.
5. Решите уравнение 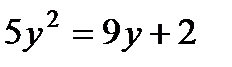 :
:
1) –2, 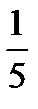 ; 2)
; 2) 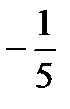 ,2; 3)
,2; 3) 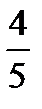 , 2; 4)
, 2; 4) 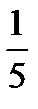 , 2.
, 2.
6. Найдите корни уравнения 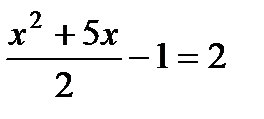 :
:
1) 1, 6; 2) –1, 6; 3) –1, -6; 4) –6, 1.
ТЕСТ 3. Теорема Виета.
1. Найдите сумму корней уравнения 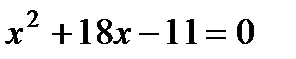 :
:
1) 18; 2) 11; 3) –18; 4) 1.
2. Найдите произведение корней уравнения 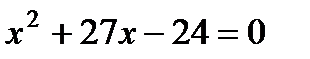 :
:
1) 27; 2) –24; 3) 1; 4) 24.
3. Найдите сумму корней уравнения 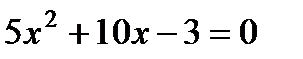 :
:
1) 10; 2) –10; 3) –2; 4) 2.
4. Найдите произведение корней уравнения 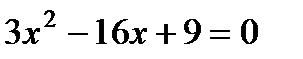 :
:
1) 3; 2) 9; 3) –9; 4) 16.
5. В уравнении 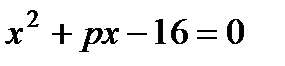 один из корней равен 8. Найдите второй корень и коэффициент
один из корней равен 8. Найдите второй корень и коэффициент 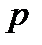 :
:
1) 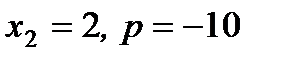 ; 2)
; 2) 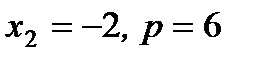 ; 3)
; 3) 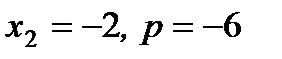 ; 4)
; 4) 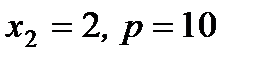 .
.
6. Один из корней уравнения 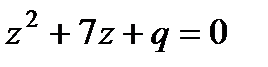 равен –2. Найдите второй корень и коэффициент
равен –2. Найдите второй корень и коэффициент 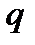 :
:
1) 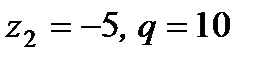 ; 2)
; 2) 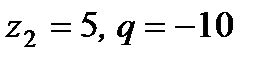 ; 3)
; 3) 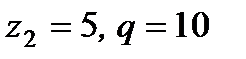 ; 4)
; 4) 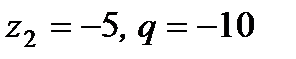 .
.
7. Найдите подбором корни уравнения 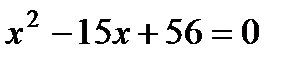 :
:
1) 4, 14; 2) –7, 8; 3) 5,10; 4) 7, 8.
ТЕСТ 4. Дробно-рациональные уравнения.
1. Какое из уравнений является дробно-рациональным:
1) 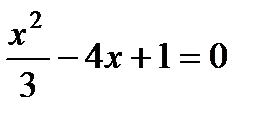 ; 2)
; 2) 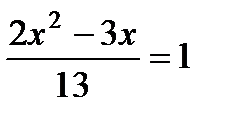 ; 3)
; 3) 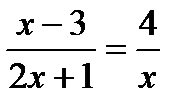 ; 4)
; 4) 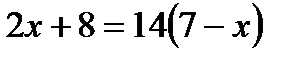 ?
?
2. Решите уравнение 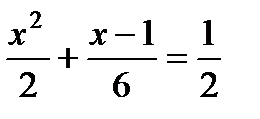 :
:
1) 2; 2) –1; 3) 1; 4) 3.
3. Решите уравнение 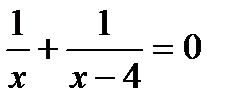 :
:
1) –2; 2) 5; 3) 2; 4) –1.
4. Найдите корни уравнения 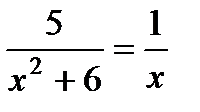 :
:
1) 1,5; 2) –2, 3; 3) –3, 2; 4) 2, 3.
5. Определите, при каком значении 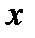 значение функции
значение функции 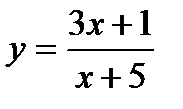 равно 2:
равно 2:
1) 4; 2) 3; 3) 8; 4) 9.
ЗАДАНИЯ ДЛЯ ПРАКТИЧЕСКОЙ РАБОТЫ
Вариант 1.
1. Решите уравнение: 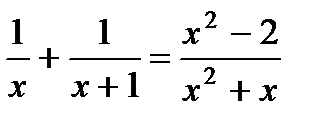 .
.
2. Решите неравенства:
а) 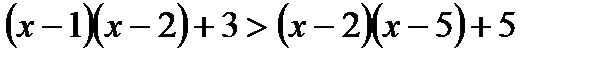 ; б)
; б) 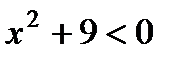 .
.
Вариант 2.
1. Решите уравнение: 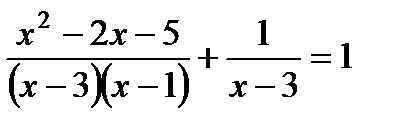 .
.
2. Решите неравенства:
а) 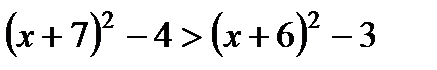 ; б)
; б) 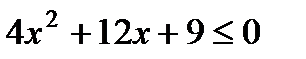 .
.
Вариант 3.
1. Решите уравнение: 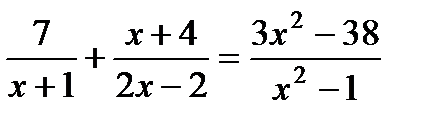 .
.
2. Решите неравенства:
а) 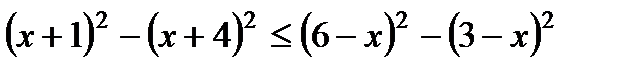 ; б)
; б) 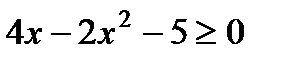 .
.
Вариант 4.
1. Решите уравнение: 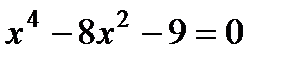 .
.
2. Решите неравенства:
а) 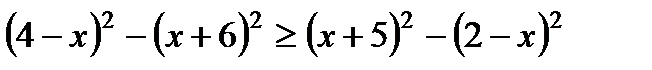 ; б)
; б) 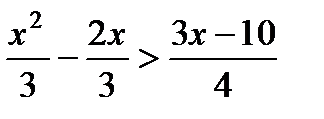 .
.
Вариант 5.
3. Решите уравнение: 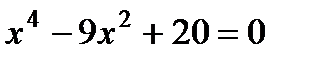 .
.
4. Решите неравенства:
а) 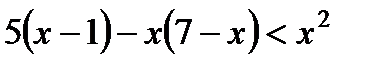 ; б)
; б) 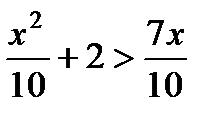 .
.
Вариант 6.
3. Решите уравнение: 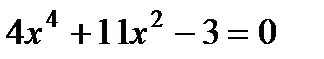 .
.
4. Решите неравенства:
а) 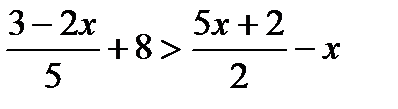 ; б)
; б) 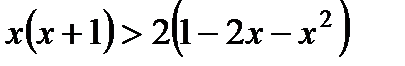 .
.
Вариант 7.
3. Решите уравнение: 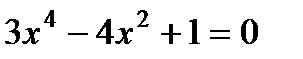 .
.
4. Решите неравенства:
а) 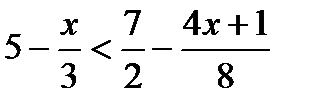 ; б)
; б) 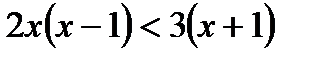 .
.
Вариант 8.
2. Решите уравнение: 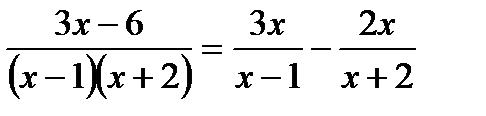 .
.
3. Решите неравенства:
а) 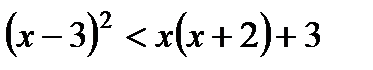 ; б)
; б) 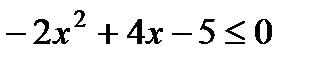 .
.
ПРАКТИЧЕСКАЯ РАБОТА №20
«Решение показательных уравнений и неравенств»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки в теме: «Решение показательных уравнений и неравенств».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Пройти все уровни тренировочного раздела.
ТРЕНИРОВОЧНЫЙ РАЗДЕЛ
«начальный» уровень:
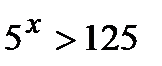
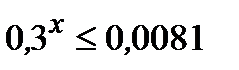
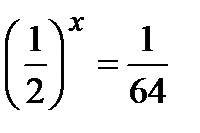

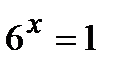
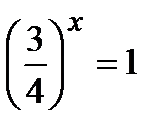
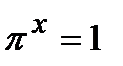
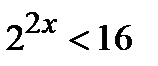
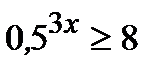
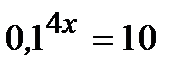
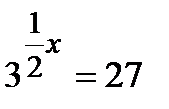
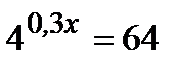
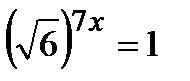
1 уровень:
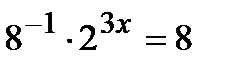
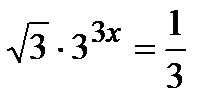
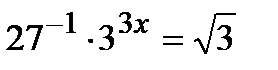
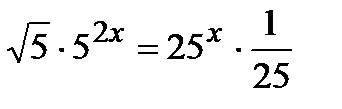
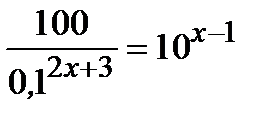
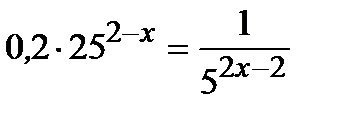
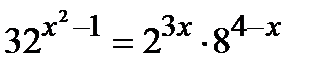
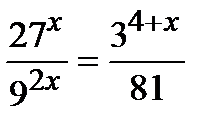
2 уровень:
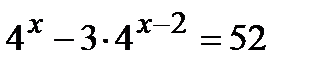
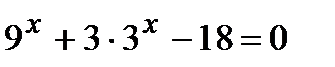
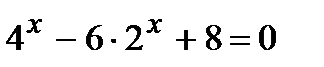
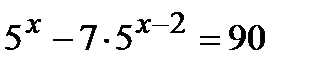
экзаменационный материал:
а) 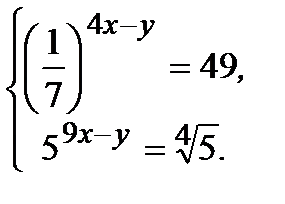 б)
б) 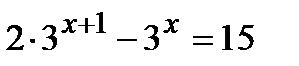 ; в)
; в) 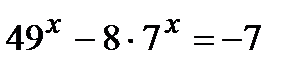 ;
;
г) 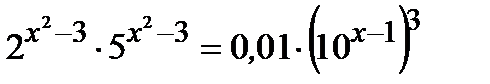 ; д)
; д) 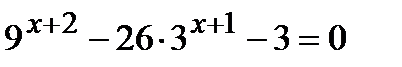 .
.
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ
Вариант 1.
1. Постройте в одной координатной плоскости графики функций 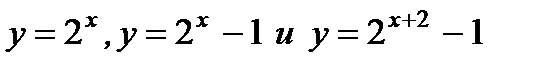 .
.
2. Решите уравнение: а) 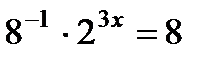 ; б)
; б) 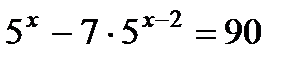 ; в)
; в) 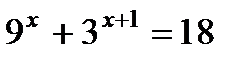 .
.
3. Решите неравенство: а) 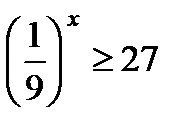 ; б)
; б) 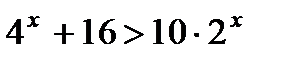 .
.
Вариант 2.
1. Постройте в одной координатной плоскости графики функций 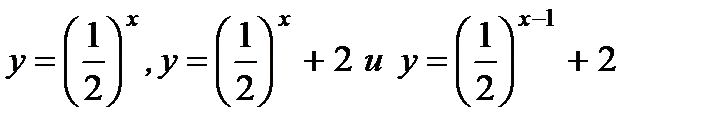 .
.
2. Решите уравнение: а) 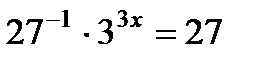 ; б)
; б) 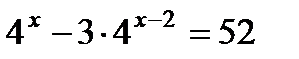 ; в)
; в) 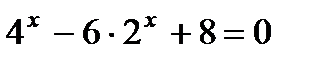 .
.
3. Решите неравенство: а) 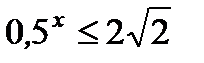 ; б)
; б) 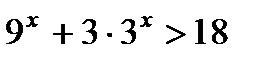 .
.
ПРАКТИЧЕСКАЯ РАБОТА №21
«Решение логарифмических уравнений и неравенств»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки в теме: «Решение логарифмических уравнений и неравенств».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Изучить памятку для решения логарифмических уравнений и неравенств.
2. Изучить условие заданий для практической работы.
3. Оформить отчет о работе.
