О математическом описании целостных объектов

Как было показано в первой главе, математическое описание сложных объектов является лишь составной частью многоуровневого описания. Но и математическое описание также может быть многоуровневым, использующим различный математический аппарат, наиболее адекватный описываемой реальности. Для описания целого как элемента и как системы, для описания его состава, структуры и интегральных характеристик, для описания статики и динамики целого требуются различные математические абстракции. Любая формальная математическая теория помимо основных постулатов, средств вывода и метрических шкал содержит также и основные идеи и системы понятий. Цель настоящего параграфа состоит в том, чтобы обсудить выбор основных математических идей, понятий и моделей, которые могут быть использованы для описания объектов и процесса восприятия.

Какой математический аппарат адекватен целостным системам? В последние десятилетия разработаны различные подходы к описанию структуры и динамики систем: теория автоматического регулирования, исследование операций, методы многомерного статистического анализа и ряд других. Для описания динамики систем используются аппарат дифференциальных уравнений, теории автоматов, алгоритмы. В качестве общей основы такого описания выступают функциональный анализ и современная алгебра.

Вероятностные и статистические методы используются в тех случаях, когда мы не располагаем полной информацией о системе или когда информация о системе несоизмерима с информационными возможностями отражающей системы, а другие пути сокращения информации не просматриваются. Статистический аппарат совершенно необходим и адекватен для описания нерегулярностей объективного мира. Когда регулярности и нерегулярности разделимы, статистические методы целесообразно использовать только для описания нерегулярного компонента.

Математические модели целостных объектов можно классифицировать как по типам этих объектов, так и по виду применяемого математического аппарата.

Описание целого как элемента. Основными инвариантами целого являются связность и ограниченность. Связное множество топологического пространства — множество, которое нельзя разбить на два непересекающихся непустых открытых множества. В этом множестве можно выделить внутренние и внешние точки. Множество внутренних точек называется областью, множество внешних — границей. Множество точек области и границы образует замкнутую область. Любые две точки области можно соединить линией, целиком состоящей из точек области.

В объектах восприятия связность между элементами может иметь место, как в пространстве объекта, так и в пространстве признаков его элементов. Пространство признаков — это множество возможных значений признаков вместе с метрикой, определенной на этом множестве. Объединение элементов в пространстве признаков может осуществляться не только в случае связности значений признаков (непрерывная шкала значений признака), но и в случае близости значений признака. Если элементы целого находятся в движении, то их признаками могут быть и характеристики движения. Взаимодействие элементов возможно вследствие связности или близости характеристик движения (например, синхронизации). Такую связность можно назвать динамической.

В общем случае могут действовать все перечисленные факторы.

Степень связности области может характеризоваться по-разному. Порядок связности — это натуральное число, равное числу внутренних областей и на единицу меньшее числа контуров. Если введена метрика, то степень связности можно оценить коэффициентом связности.

Множество ограничено, если включает в себя границу. По характеристике ограниченности связные множества делятся на открытые и замкнутые. Замкнутое множество содержит все свои предельные точки. Открытое множество не содержит предельных точек. Множество, включающее в себя лишь часть предельных точек, называется полуоткрытым. Если множество конечно, ограниченно и замкнуто, то оно компактно. Множество называется выпуклым, если любые две его точки могут быть соединены отрезком прямой, все точки которого принадлежат данному множеству.

Понятия связности, ограниченности, компактности, выпуклости являются тем основным набором математических понятий, с помощью которого можно описать основные свойства целого как элемента. Понятия эти могут быть дифференцированы, далее для их оценки можно вводить количественные меры.

Целое как элемент может быть описано и как математическое отношение. Устанавливается множество наблюдаемых признаков целого P(Р₁, P₂, ..., P_n) в области их значений X(X₁, X₂, ..., X_n), определяются допустимые комбинации значений. Тогда целое C описывается отношением

C ⊂ X₁ × X₂ × ... × X_n

С точки зрения логики целое — элемент может рассматриваться как конъюнкция свойств, с одной стороны, и член родовидового отношения — с другой. Объект как конъюнкция есть конъюнкция противоположностей по одной характеристике, и конъюнкция разных характеристик. Как член родовидового отношения объект характеризуется объемом и содержанием.

Целое как система (Алгебраическое описание). Объект рассматривается как конечное множество элементов. Элементами являются как области, так и границы. Как известно, множество задается перечислением элементов или указанием признака принадлежности к данному множеству. Далее будем считать, что множество элементов целого задано перечислением и тем самым определен его состав. Элементы могут иметь некоторое (конечное) число независимых характеристик (признаков) — качественных, порядковых и количественных. Между элементами существуют отношения различного типа. Отношением называется всякое подмножество декартова произведения конечного числа множеств. В алгебре рассматриваются отношения пяти типов: эквивалентности, толерантности, строгого порядка, квазипорядка и нестрогого порядка [61]. Отношения эквивалентности рефлексивны, симметричны и транзитивны. Отношения толерантности рефлексивны и симметричны, отношения строгого порядка транзитивны и антирефлексивны. Отношения квазипорядка рефлексивны и транзитивны. Отношения нестрогого порядка рефлексивны и антисимметричны. В зависимости от числа элементов, входящих в отношение, их называют унарными, бинарными, тернарными и для множества элементов — полиарными. Отношения задаются перечислением подмножеств, для которых верно данное отношение. Бинарные отношения можно задать матрицей или графом. Отношение эквивалентности задает разбиение множества на классы. Отношения порядка устанавливаются: только для некоторых пар элементов (не все элементы сравнимы). В случае нестрогого порядка все элементы сравнимы.

Сравнимость означает наличие общего признака. Рефлексивность означает истинность выражения xAx. Симметричность означает выполнение отношений xAy и yAx, для асимметричных отношений, по крайней мере, одно из них не выполнено. Транзитивность означает, что если xAz и zAy, то xAy.

В связи с этой классификацией отношений на основе их свойств отметим, что эта система отношений не является полной в том смысле, что могут быть определены отношения, не принадлежащие ни к одному из перечисленных классов. Каждое отношение есть некоторое ограничение. Например, объекты, толерантные между собой, должны удовлетворять условиям рефлексивности и симметричности. Но эти ограничения довольно слабы в смысле, что соотносимые объекты могут изменяться в весьма широких пределах без нарушения этих условий.

Для содержательной характеристики близости объектов некоторого множества необходимо вводить качественные и количественные характеристики близости. Эти характеристики могут быть, весьма, различными, например, это может быть расстояние в пространстве признака, наличие общей меры, простота преобразования одного элемента в другой и т. д. Таким образом, алгебраические отношения, наложенные на множество элементов, представляют собой лишь каркас, внутри которого имеется еще достаточно большая свобода для варьирования свойств элементов.

Качественные, сравнительные и измерительные признаки в терминах отношений, существенно, различны [62]. Качественные (классификационные) признаки устанавливаются на основе понятия эквивалентности любым непротиворечивым образом, независимо от того, существуют такие классы в действительности или нет. Сравнительные признаки должны удовлетворять отношениям частичной упорядоченности и фактам природы. Количественные признаки устанавливаются методом счета или методом измерения. Для измерений должна быть указана объективная процедура. Измерение, в отличие от сравнения, требует уже системы отсчета, которая выбирается из реальных условий физического мира. Следует различать отношения на множестве элементов объекта и отношения на множестве словаря элементов (отношения на множестве слов в предложении и отношения на множестве слов в данном языке). Отношения второго типа изучаются семиотикой и в данном контексте не рассматриваются. Однако отметим, что проблема связи между отношениями в языке и отношениями в целом, построенном на основе этого языка, представляет несомненный интерес применительно к описанию целого. В известном смысле, это есть отношение между синтактикой и семантикой, возможным и существующим.

Отношениями связаны все элементы целого. Инвариантные отношения определяют структуру динамического объекта. Структура — функция декомпозиции и признака, по которому устанавливается отношение порядка. Математически структура описывается ориентированным графом, вершины которого соответствуют элементам, а дуги — отношениям. Частным случаем графа является дерево, которое соответствует иерархической структуре. Иерархическая структура характеризуется числом уровней, модулем иерархии (отношение числа элементов на смежных уровнях) и весами ветвей. Для реальных систем эти величины ограничены и в каждом конкретном случае могут быть указаны их оптимальные значения. Веса ветвей различных уровней взаимосвязаны. Динамика процессов в иерархии характеризуется различной полосой пропускания частот различных уровней.

Вопрос о числе компонентов иерархии связан с вопросами числа существенных переменных и числа однородных (и разнородных) компонентов целого. Проблема эта сводится к поиску критерия полноты эмпирических или теоретических характеристик, как по общему их числу, так и по составу. При этом полнота понимается в смысле полноты обеспечения необходимого разнообразия, полноты состава целого, необходимой для выполнения его функций. Многие практические задачи, связанные со структурой и функционированием целостных систем, сводятся к решению задачи определения экстремума (максимума) некоторой (целевой) функции в рамках ограничений, наложенных на ее аргументы. Как известно, общих методов решения этой задачи не существует. В зависимости от имеющейся информации приходится применять разные методы — алгоритмические, поисковые или эвристические. Трудность задачи быстро растет с увеличением числа аргументов целевой функции. Выбор целевой функции, критерия качества также иногда бывает непростой задачей. Целое как система содержит помимо непрерывных и линейных компонентов также дискретные и нелинейные компоненты, что сильно затрудняет математическое описание целого.

Математическое описание динамики целостных систем. В контексте данной работы динамика целостных систем нас будет интересовать в двух аспектах: во-первых, динамической системой является воспринимающий человек; во-вторых, человек может иметь дело с отображением динамической системы.

В настоящее время имеется хорошо разработанный математический аппарат для описания динамики, анализа и синтеза систем весьма широкого класса (теория автоматического управления, теория оптимального управления, теория автоматов, общая теория систем, исследование операций, системотехника и другие). Состояние системы характеризуется набором обобщенных координат, ее поведение — изменением обобщенных координат во времени. Во многих случаях при описании реальных систем возникает необходимость упрощения описания, но упрощения такого, которое сохраняло бы существенную информацию о поведении системы. Два обстоятельства, на которые обратил внимание А. М. Молчанов, помогают произвести упрощение. Он пишет [63]: «...нет надобности рассматривать (по крайней мере, в первом приближении) сразу всю иерархию масштабов и соответствующих им систем. Факт „замирания“, „выключения“ и высших, и низших масштабов времени имеет первостепенное методологическое значение. Он позволяет сводить вопрос к изучению только одной ступеньки, содержащей только два соседних масштаба времени». В другой работе [64] он же отметил, что значимость взаимосвязанных переменных быстро убывает, поэтому часто можно ограничиться небольшим их числом, не совершая при этом грубой ошибки.

Рассмотрим влияние связности на свойства динамической: системы, в частности, на ее устойчивость. Понятие «устойчивость» неоднозначно. Устойчивостью называют способность объекта сохранять неизменными свою целостность, структуру, функцию или пределы изменения существенных переменных при заданном внешнем воздействии. Система может быть одновременно устойчивой в одном и неустойчивой в другом смысле. Например, она может быть целой, но неспособной выполнять свои функции из-за чрезмерно больших колебаний существенных переменных, превышающих область допустимых значений. Часто для обеспечения функциональной устойчивости в изменяющейся среде необходимо изменять параметры или структуру системы (самонастраивающиеся и самоорганизующиеся системы). Математическая теория динамической устойчивости позволяет сделать вывод о том, что неустойчивость системы возрастает с увеличением системы и ее связности. Введение иерархии уменьшает число связей в системе и делает ее более устойчивой.

Проблемы анализа и синтеза целостных систем являются главными задачами общей теории систем и ее разделов (теории автоматов, теории систем автоматического управления). Разработаны методы синтеза искусственных систем некоторых классов и предложены модели эволюции некоторых простейших естественных систем.

Интегральные характеристики целостного объекта. Интегральные характеристики целого определяются его составом и структурой, свойствами частей и отношений. Интегральные характеристики суть функционалы, определенные на множестве элементов объекта. Как уже говорилось, целое есть нечто большее, чем сумма своих частей. Известно, что Аристотель считал это определяющим признаком целого.

Анализ целостных объектов показывает, что они обладают не только аддитивными, но также супераддитивными (данная характеристика целого больше суммы соответствующих характеристик частей) и инфрааддитивными (данная характеристика меньше суммы своих частей) свойствами. Некоторые из таких интегральных характеристик можно определить как линейные (аддитивные) или нелинейные (неаддитивные) функционалы.

Действительный функционал с геометрической точки зрения есть отображение пространства любого числа измерений в одномерное пространство (на числовую прямую). Интегральные характеристики целостного объекта всегда определяются на множестве всех его элементов. В этом смысле интегральные характеристики — всегда глобальные функционалы. Частным случаем функционалов являются линейные функционалы.

Рассмотрим некоторые подходы к количественной оценке разнообразия, регулярности, сложности и некоторых других интегральных характеристик целостных объектов. Для этого необходимо задаться некоторыми характеристиками отражающей системы; выбрать модели объектов и уточнить определение конкретных интегральных характеристик.

Существенными характеристиками отражающей системы будет поле контакта с объектом, объем памяти и набор операций, которые может выполнять система. В качестве моделей было бы полезно использовать такую их последовательность: линейные последовательности букв или цифр, кольцевые последовательности букв или цифр, линейные и кольцевые последовательности векторов, неупорядоченное и частично упорядоченное множество векторов, плоскостные геометрические объекты.

Рассмотрим меры разнообразия. Будем различать разнообразие состава и разнообразие структуры. При любой оценке разнообразия необходимо указать тот предел, при достижении которого объекты становятся неразличимыми. Например, таким пределом может служить инвариант подобия: все подобные объекты считаются неразличимыми.

При анализе состава следует иметь в виду, что в состав могут входить не только непересекающиеся элементы, на которые разбивается целое в результате декомпозиции, но также и объединения элементов, включая и целое. В таком случае уже имеет значение порядок элементов. В этом одна причина непригодности энтропийной оценки. Следует также различать разнообразие состава областей и границ.

Введем меру разнообразия состава ограниченной одномерной последовательности из неметрических элементов. Дан конечный алфавит длины m. Из букв этого алфавита составим последовательность конечной длины. Очевидно, что наименьшим разнообразием будет обладать последовательность, состоящая из одинаковых букв, а наибольшим — последовательность, в которой все буквы различны. Очевидно также, что разнообразие состава увеличивается с увеличением длины последовательности только в том случае, если при этом появляются новые буквы. Поэтому целесообразно выбрать за нулевую точку шкалы разнообразие последовательностей, состоящих из одинаковых букв, а за верхнюю точку шкалы — разнообразие последовательностей, в которых все буквы разные. Примем всю шкалу за единичный отрезок. Тогда вышеуказанным требованиям удовлетворяет следующая мера разнообразия состава: в среднем на одну букву

r = (n - 1) / (N - 1),

где n — число различных букв в последовательности, N — длина последовательности. При (N ≠ 1 и n = 1), r = 0; при (n = N ≠ 1), r = 1; при (n = N = 1), r = 0/0, т. е. неопределенность. Действительно, при одном элементе нельзя говорить о разнообразии состава. Соответственно для всей последовательности разнообразие

R = N × (n -1) / (N - 1).

Из этой формулы следует, что при простом удвоении последовательности разнообразие ее состава практически не увеличивается. Введенные меры разнообразия состава не зависят от порядка и относительных частот букв в последовательности.

До сих пор мы исходили из неявного предположения о том, что все буквы равноценны (имеют равную длительность, занимают одинаковую площадь, имеют одинаковую значимость и т. д.). Но это может быть и не так. Неравноценность букв может быть учтена путем введения весовых коэффициентов. При этом будут видоизменены и формулы для оценки разнообразия состава. Как мы видим, оценка разнообразия состава последовательности заметно отличается от информационных оценок.

В последовательности человек воспринимает не только отдельные буквы, но и группы букв, блоки, причем имеется тенденция ко все большему укрупнению блоков. Укрупняя блоки последовательности, можно построить такую иерархию блоков, верхним уровнем которой будет «блок» всей последовательности. Для оценки разнообразия такой иерархии можно предложить аддитивную оценку вида

r_i = 1 / (k - 1) ∑_i-1^k-1 (n_i - 1) / (N_i - 1)

где k — число уровней иерархии, i — порядковый номер уровня.

Для любого k при (n_i = 1 и N_i ≠ 1), r_i = 0; при n_i = N_i ≠ 1, r_i = 1. Случай n_i = N_i = 1 вырожденный.

Так как иерархия определяет одну из возможных структур последовательности, то величина r_i является оценкой разнообразия не только состава, но и этой конкретной структуры.

Если последовательность не ограничена и наблюдается ее конечный отрезок, то нельзя говорить о разнообразии ее состава в вышерассмотренном смысле. Можно оценить алфавит для стационарных последовательностей, безусловные и условные вероятности и энтропии и по ним судить о степени регулярности последовательности. Рассмотрим простой пример последовательности, состоящей из нулей и единиц. Регулярность (закономерность) в такой последовательности может состоять в ее периодичности. Если для таких последовательностей с различной степенью регулярности вычислить ряд значений энтропии H₀, H₁, H₂ и т. д., то для этих последовательностей соответствующие им ряды окажутся различными. Однако вычисление энтропии высоких порядков связано с большими техническими трудностями. Поэтому для оценки нерегулярности в целостном объекте целесообразно применять другие способы (меры асимметрии, аритмии и т. п.).

Если элементами последовательности являются метризованные элементы, например числа, то между ними могут быть установлены отношения порядка. В этом случае меры разнообразия структуры должны учитывать и эти отношения, но могут быть введены специальные меры упорядоченности. На множестве элементов последовательности могут быть заданы системы операций, с помощью которых получаются новые элементы. Это еще более затрудняет оценку разнообразия структуры.

Если элементы последовательности (или любого целостного объекта) многомерны, то возможны два подхода к оценке разнообразия состава: сведение многомерной модели к одномерной путем увеличения алфавита или сведение n-мерной модели к системе n одномерных моделей.

В каком отношении меры разнообразия находятся к другим интегральным характеристикам? Меры упорядоченности характеризуют одну из структур — структуру порядка. Меры однородности характеризуют главным образом состав, его распределение в пространстве. Меры регулярности характеризуют возможность обратимого сокращения разнообразия.

В работах, посвященных восприятию, все чаще фигурирует понятие «отображение». Его применение представляется весьма целесообразным и продуктивным, если имеется в виду математическое содержание этого понятия.

Восприятие целостного объекта можно рассматривать как отображение объективного множества — объекта в субъективное множество — образ. Множество-объект является подмножеством перцептивного пространства, множество-образ — подмножеством субъективного пространства. Такая интерпретация восприятия целостного объекта позволяет описать его в терминах отображения множества.

Понятие «отображение» в математике является синонимом понятий «преобразование», «функция», «оператор». Во всех случаях для определения отображения нужно задать: два произвольных непустых множества (X и Y), правило, закон соответствия элементов этих множеств Y=f(X), подмножество D_f — область определения функции f, подмножество R_f — область значений функции f (рис. 2) [65]. Для каждого подмножества A из D_f функция f ставит в соответствие некоторое подмножество В из R_f. Подмножество A называется прообразом, подмножество B — образом A.

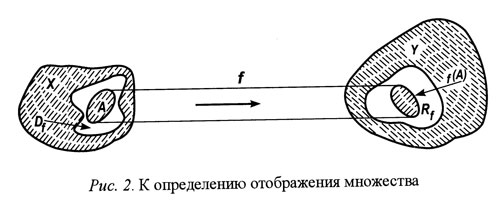
Конкретный вид отображения определяется многими факторами, главными из которых являются: мощность и другие характеристики множеств, между которыми устанавливается соответствие; вид функции, область определения функции. Соответствие между элементами одного и того же множества называется отображением в себя. Частным случаем отображения является взаимнооднозначное соответствие (изоморфизм). Многие преобразования образуют группу. Преобразования могут быть непрерывными и дискретными, параллельными и последовательными. Преобразователи могут иметь память и не иметь ее. Преобразования без памяти каждому подмножеству A ставят в соответствие всегда одно и то же подмножество B. Результат преобразования с памятью зависит, кроме исходного множества, также от состояния преобразователя в момент функционирования.

Восприятие целостного объекта (отображение I) и целенаправленное действие, поведение, продуктивная деятельность (отображение II) являются частными, но весьма сложными видами отображений. Хотя при их описании математические понятия весьма полезны, однако, для полного их математического описания современный аппарат недостаточен. Одно из преимуществ применения математических понятий состоит в том, что с их помощью в таких разных психических процессах, как отражение и поведение, восприятие и действие, познание и творчество, отражение и преобразование, можно обнаружить общее, описать их на одном языке.

Глава III

АНАЛИЗ ОБЪЕКТОВ ВОСПРИЯТИЯ