ДУ высших порядков, допускающие понижение порядка.

ДУ порядка выше 1-го наз.ДУ высших порядков.

Отдельные виды ДУ высших порядков удается проинтегрировать путём понижения порядка уравнения.

1.Уравнение вида

y⁽ⁿ⁾=ò(x), решают путём n– кратного интегрирования.

2. Уравнение вида

F(x, y^(k), y^(k+1),…, y⁽ⁿ⁾)=0, явно не содержащее искомой функции и её первых производных до k-1 включено, сводят к уравнению порядка n-k путём введения новой неизвестной функции z=z(x),пологая z=y^(k).Тогда уравнение примет вид

F(x, z, z^’,…, z^(n-k))=0.

3. Уравнение вида

F(y, y^’, y^’’,…, y⁽ⁿ⁾)=0, явно не содержащее независимой переменной х, интегрируют с помощью подстановки y^’=p, где р=р(у) – новая неизвестная функция, а за аргумент временно примем переменную у. Тогда

,

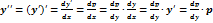т.е. .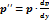

Аналогично можно получит

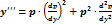и т. д.

При этом порядок уравнения понижается на единицу.

Линейные однородные ДУ 2-го порядка с постоянными коэффициентами. Структура общего решения в зависимости от корней характеристического уравнения.

Уравнение вида

a₂y^’’+a₁y^’+a₀y=0, (*)

где a_iÎR, i=0, 1, 2,наз. линейным однородным (ЛОДУ) 2-го порядка с постоянным коэффициентом.

Теорема.(структура общего решения ЛОДУ 2-го порядка). Если два частных решения y₁=y₁(x)и y₂=y₂(x) ЛОДУ(*)образуют на интервале (а;b) фундаментальную систему, то общим решением этого уравнения явл. функция

y=C₁y₁+C₂y₂ ,(**)

где С₁и С₂ – произвольные постоянные.

Т. о. для нахождения общего решения ЛОДУ (*) достаточно найти два его частных решения образующих фундаментальную систему.

Будем искать частные решения уравнения(*)в виде y=e^lx,где l - некоторое число (Л. Эйлер).

Дифференцируем эту функцию два раза и подставляя выражение для y, y^’, y^’’в уравнение (*), получим:

a₂l²e^lx+a₁le^lx+a₀e^lx=0 |¸e^lx¹ 0

a₂l²+a₁l+a₀=0, (***).

Уравнение(***)наз. характеристическим уравнением (х. у) ЛОДУ (*)(для его составления достаточно в уравнении (*) заменить y^’’, y^’, yна l², l, 1 соответственно).

При решении х. у. (***)возможны следующие три случая:

1)D>0;

2) D=0;

3) D<0.

Линейные неоднородные дифференциальные уравнения (ЛНДУ) 2-го порядка с постоянными коэффициентами. Структура общего решения.

Уравнение вида

a₂y^’’+a₁y^’+a₀y= f(x), (*)

где a₁ÎR, i=0, 1, 2 f(x) – непрервная на некотором интервале (а;b) функции.

Правая часть f(x)	Корни характеристического уравнения	Вид частного решения
Pn(x)	1. Число 0 не явл. корнем х. у.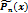
2. Число 0 – корень х. у.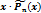
Pn(x)×eax	1. Число a не явл. корнем х. у.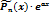
2. Число a– корень х. у.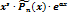
Pn(x)cosbx+Qm(x)sinbx	1. Число ±biне явл. корнем х. у.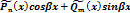
2. Число ±bi– корень х. у.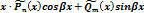
aax× (Pn(x)cosbx+Qk(x)sinbx)	1. Число a±bне явл. корнем х. у.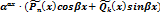
2. Число a±b– корень х. у.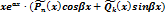

Замечание 1.k=max(m, n).

Замечание 2.

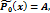
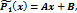
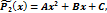
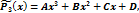и т. д.,

где A, B, C, D, … - неизвестные коэффициенты, которые находят подстановкой в уравнение (*)и приравниванием коэффициентов при одноимённых функциях в левой и правой частях равенства.

67. Понятие функции двух переменных. Область определения.

Пусть каждой упорядоченной паре чисел (х, у) из некоторой области D соответствует определённое число zÎEÌR. Тогда z=f(x, y)наз. функцией двух переменныхх и у, х, у – независимыми переменными или аргументами, D – областью определения, а множествоЕ всех значений функции – областью её значений. Геометрически область определения функции z=f(x, y) представляет собой либо всю плоскость Оху, либо некоторую часть плоскости Оху ограниченную линиями, которые могут принадлежать или не принадлежать этой плоскости.

Линию, ограничивающую область наз. границей области. Точки области, не лежащие на границе наз. внутренними. Область состоящая только из одних внутренних точек наз. открытой. Область с присоединённой к ней границей наз. замкнутой, и обозначается 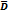.