Дифференциальные зависимости при изгибе

Изгибающий момент, поперечная сила и интенсивность распределенной нагрузки связаны следующими зависимостями (зависимостями Д.Н.Журавского):

Выводы:

1 Если на некотором участке балки отсутствуюет распределенная нагрузка (q=0), то эпюра Q – прямая, параллельная к оси абсцисс (Q=const), а эпюра М на этом участке наклонная прямая.

2 Если на некотором участке есть равномерно распределенная нагрузка, то эпюра Q – наклонная прямая, параллельная оси абсцисс (Q=const), а эпюра М – парабола

3 Если на некотором участке балки:

Q > 0, то изгибающий момент возрастает,

Q < 0, то изгибающий момент убывает,

Q = 0, то изгибающий момент постоянный

4 Если поперечная сила, изменяясь по линейному закону, проходит через нулевое значение, то в соответствующем сечении изгибающий момент будет иметь экстремум.

5 Под сосредоточенной силой на эпюре Q образуется прыжок на величину приложенной силы, а на эпюру М – резкое изменение угла наклона соседних участков.

6 В сечении, где приложена пара сил, эпюра М будет иметь прыжок на величину момента пары. На эпюре Q это не отразиться.

7 Если равномерно распределенная нагрузка направлена вниз (вторая производная, которая характеризует кривизну линии), эпюра М обращена выпуклостью вверх, навстречу нагрузке.

СЛОЖЕНИЕ ПАР СИЛ. УСЛОВИЕ РАВНОВЕСИЯ ПАР.

Теорема. Система пар, действующих на тело в одной плоскости, эквивалентна паре сил с моментом, равным алгебраической сумме моментов пар системы.

Допустим, на тело действуют три пары (рис. а), моменты которых 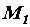, 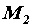и и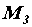звестны. Каждую из заданных пар заменим эквивалентной парой соответственно 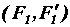, , 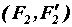, 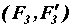но с одинаковыми плечами 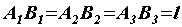, т. e. 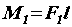, , 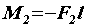, 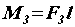и расположим эти пары так, чтобы их силы действовали вдоль двух параллельных прямых (рис. б).

Как известно, равнодействующая сил, действующих вдоль одной прямой, направлена по той же прямой и модуль ее равен алгебраической сумме составляющих сил. Поэтому, сложив силы, приложенные к точкам 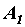, , 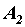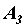и к точкам 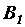, , 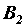, 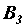получим равнодействующую пару 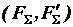, эквивалентную трем заданным парам (рис. в). При этом .

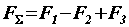Момент равнодействующей пары ,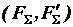

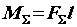а так как 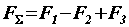, то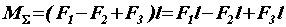
или 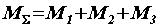. Теорема доказана.

Распространяя равенство 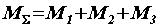на любое число пар, действующих на тело, можем записать
.

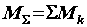Следовательно, для того чтобы сложить любое число пар, действующих на тело в одной плоскости, достаточно алгебраически сложить моменты этих пар. Полученный в результате сложения момент 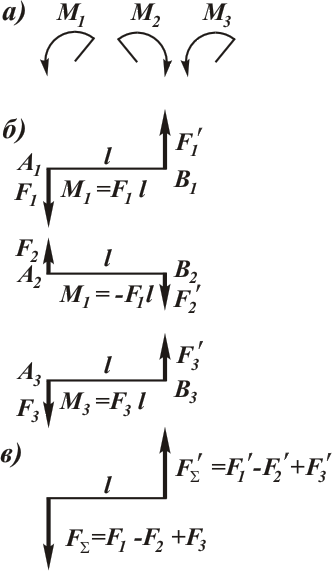и определяет равнодействующую пару сил.

Если в результате сложения пар 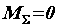, то действующие на тело пары образуют уравновешенную систему. Следовательно, необходимое и достаточное условие равновесия системы пар выражается одним уравнением
,

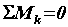Т. е. для равновесия системы пар сил, действующих на тело в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма их моментов была равна нулю.

Значит, систему пар или одну пар можно уравновесить только парой.