Число степеней свободы(ЧСС) механизма. Подвижность механизма.

Если на движущиеся звенья в пространстве не наложено никаких связей, то ЧСС=6, тогда К звеньев, образующих кинематическую цепь до их соединения в кинематическую пару будут иметь 6К степеней свободы.

В общем случае кинематическаяцепт может содержать 1-5 степеней свободы.

Общее ЧСС, наложенных всеми кинематическими парами, входящими в цепь:

5P₅+4P₄+3P₃+2P₂+1P₁

P_i- число пар i-го класса

ЧСС определяется по формуле:

H=6K-5P₅-4P₄-3P₃-2P₂-1P₁

H-число степеней свободы механизма.

При соблюдении определенных условий кинематическая цепь может стать механизмом.

Звенья кинем.цепи обладает определенностью движения только при наличии неподвижного звена.

Т.о. наличие неподвижного звена-обязательное условие существования механизма.

Степень подвижности механизма (пространственная) определяется по формуле Сомова-Малышева:

W=6n-5P₅-4P₄-3P₃-2P₂-1P₁

n-число звеньев

Cтепеньподвижности(плоская) по формуле Чебышева:

W=3n-2P₅ – P₄

(сопромат)

9. Однородное растяжение бруса как пример реализации одноосного напряженного состояния материала. Центральное (осевое) растяжение/сжатие вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. В этом случае все внутр. силовые факторы, кроме фактора растягивающей/сжимающей силы, =0, т.е. возникает только один внутр. силовой фактор – продольная сила N_z/N. Прямые брусья, работающие на растяж./сжатие часто наз. стержнями. Продольные силы, соответствующие деформации растяжения,–знак+, деф.сжатия–знак–.

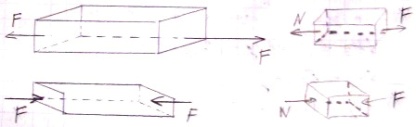
При растяжении прод. сила направлена от сечения, при сжатии – к сечению. Модуль и направление (знак прод. силы) опред. из ур-ния равновесия, составленного из отсеченной части бруса: ∑Z=0. N+∑F_iz=0 → N= –∑F_iz

Продольная сила в поперечном сечении бруса – равнодействующая внутренних нормальных сил, возникающих в этом сечении. N=σA

В тех случаях, когда прод. силы в различных поперечных сечениях бруса неодинаковы, закон их изменения по длине бруса предст. в виде графика – эпюра прод. сил (график ф-ции N=f(z)). Исп-ся при расчете прочности.

При растяжении/сжатии бруса, в его поперечных сечениях возникают только нормальные напряжения σ=N/A. При растяжении напряжение +, при сжатии–.

В местах резкого изменения формы и размера поперечного сечения бруса возникают местные напряжения – явление ”концентрация напряжения”. В тех случ., когда норм.напряжения в различных поперечных сечениях неодинаковы, целесообразно показывать закон их изменения по длине бруса в виде графика – эпюры норм. напряжений.

(теория механизмов и машин)

10.Структурный синтез и анализ механизмов.Структ.синтез механизма сост.в проектировании его структурной схемы(схема, указывающая стойку,подвижные звенья, виды кинематич. пар и их взаимное расположение).

Принцип Ассура. Более сложный рычажный механизм можно образовать путем присоединения открытых кинематических пар к исходному механизму. Мех-м, звенья кот. соединены с помощью низших кинем.пар – рычажный, стержневой. Структурная группа (группа Ассура) – кинематическая цепь, число степеней свободы которой =0 после присоединения ее внешними кинематич. парами к стойке, и которая не распадается на более простые цепи, удовлетворяющие этому условию.

Для структурных групп плоских механизмов с низшими парами w=3n-2P_н (w – степень подвижности пространственного механизма,P_н – число звеньев; при w=0 P_н =3n/2)

n				…
Pн				…

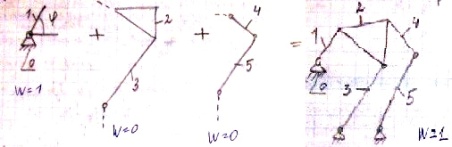
Простейшая – структурная группа, у кот. n=2, P_н=3 – структурная группа 2го класса. Порядок структ.группыопред. числом элементов ее внешних кинемтических пар, которыми она может присоединяться к механизму. Все группы 2го класса явл. группами 2го порядка. Структ.группы, у кот. n=4, P_н=6 м.б. 3го или 4го класса. 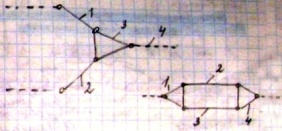В общем случае класс структ.группыопред.числомкинематич.пар в замкнутом контуре, образованном внутренними кинематич.парами. Класс механизма опред. высшим классом структ.группы, входящей в его состав.

Порядок образования механизма записывается в виде формулы его строения: I(0;1) →II(2;3)+ II(4;5) – механизм 2го класса(2й класс, 2 порядок, 1 вид).