Базовый алгоритм вычисления индекса

Пусть состояние многомерной системы характеризуется вектором индикаторов X=[x₁,…,x_n]. Пусть имеется набор из m векторов X_k, k=1,2,…,m, с известными значениями индикаторов. Предлагается следующий базовый алгоритм вычисления индекса данной системы.

1. По исходным данным формируется матрица A=[X₁,…,X_m]^T размерности m×n, где m – количество объектов, которые соответствуют строкам матрицы, а n – количество параметров (индикаторов), которые соответствуют столбцам матрицы.

2. Методом сингулярного разложения матрицы A вычисляется k-й правый сингулярный вектор V_k=[ν₁,…,ν_n]_k, который соответствует k-му сингулярному числу матрицы s_k.

3. Для любого входного (распознаваемого) вектора Z размерности n×1 вычисляется его энергия связи с вектором V_k=[ν₁,…,ν_n]_k:

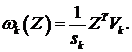(1)

4. Искомое значение индекса вычисляется по следующей формуле:

I_k(Z)=c₀+c₁ω_k. (2)

Рассмотрим важное математическое свойство базового алгоритма.

Предложение 1. Если входной вектор совпадает со строкой матрицы A: 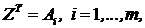то значение энергии связи в точности совпадает с соответствующей компонентой левого сингулярного вектора U_k=[u₁,….,u_m]_k : ω_k(A_i)=u_ki.

Значения коэффициентов c₀ и c₁ индекса I_k(Z), а также номер k правого сингулярного вектора в уравнении (2) могут определяться двумя способами:

1) экспериментально (на основе экспертных оценок) в соответствии с особенностью приложения;

2) как решение задачи параметрической оптимизации для определения значений коэффициентов индекса.

Рассмотрим решение второй задачи на основе среднеквадратического критерия качества.

Пусть имеется матрица M=[ω_kj] размерности (p×m), где k=1,…,p и p – количество сингулярных векторов, используемых для расчета индекса, а j=1,…,m и m – количество обучающих векторов. При этом значение элементов данной матрицы вычисляются по формуле (1) базового алгоритма для обучающих векторов.

Представим задачу в векторно-матричном виде:

MC=B, (3)

где C ‑ вектор коэффициентов индекса размерности (m×1):

C=[c_m-1,…, c₁,c₀]^T,

вектор B ‑ вектор размерности (p×1), компонентами которого являются заданные значения индекса для обучающей выборки:

B=[b₁,…,b_p]^T.

Рассмотрим сингулярное разложение матрицы M:

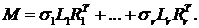(4)

Определим матрицу M⁺ следующим образом:

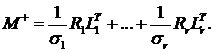(5)

Предложение 3. Матрица M⁺ определяет решение уравнения (3) в следующем виде:

C=M⁺B. (6)

Доказательство: Умножим обе части уравнения (6) слева на матрицу M⁺:

M⁺MC=M⁺B. (7)

Умножим обе части полученного уравнения (7) слева на матрицу M:

MM⁺MC=MM⁺B. (8)

Учитывая в левой части (8) условие М⁺М=Е, получаем

,

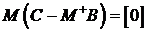где 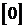‑ нулевой вектор размерности (p×1).

Так как исходная матрица М тождественно не равна нулю, получаем решение (6), что доказывает справедливость Предложения.

Предложение 4. Формула (6) дает решение уравнения (3) в смысле минимума среднеквадратической ошибки:

Q= (MC ‑ B)^T(MC ‑ B). (9)

Доказательство: Для доказательства определим в явном виде вектор коэффициентов C таким образом, чтобы минимизировать квадратичный критерий качества (9):

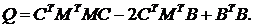
По правилам векторно-матричного дифференцирования, возьмем производную от Q по C и приравняем ее нулю:

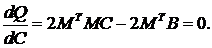(10)

Из полученной системы алгебраических уравнений (10) определим вектор коэффициентов C:

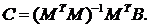(11)

Получим выражение для правой части (11) через компоненты сингулярного разложения.

Транспонированная матрица M^T имеет следующий вид:

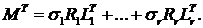(12)

Сформируем произведение M^TM:

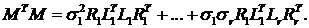
С учетом условий ортогональности для правых и левых сингулярных векторов получим:

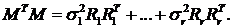(13)

Так как матрица (13) симметричная, то обратная матрица представляется в виде

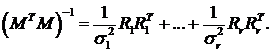(14)

Сравнивая (14) с (5) получаем:

M⁺= (M^TM)^-1M^T,

что и требовалось доказать.

Матрица M⁺ называется псевдообратной матрицей (Мура-Пенроуза) для матрицы M. В зависимости от соотношения размерностей выражение для нахождения псевдообратной матрицы будет различным:

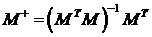· при p≥m;

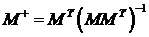· при p<m;

· M⁺= M^-1 при p=n (псевдообратная матрица равна обратной матрице).

На основе сингулярного разложения, нетрудно проверить, что матрица M⁺ удовлетворяет следующим четырем условиям Мура-Пенроуза [9]:

.

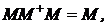
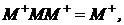
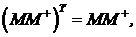
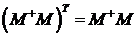Важным свойством представления M⁺ через компоненты сингулярного разложения является то, что задача определения оптимальных коэффициентов C индекса решается на основе сингулярного разложения матрицы M, которое выполняется теми же процедурами базового алгоритма вычисления индекса.

Выражение для оптимального вектора коэффициентов C через компоненты сингулярного разложения имеет вид:

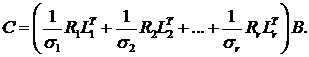(14)

Ниже представлены частные случаи процедуры формирования индекса с использованием компонент сингулярного разложения матрицы М.

Одномерный линейный случай

Для этого случая обучающая система уравнений (2) имеет следующий вид:

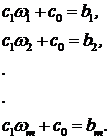. (15)

При векторно-матричном представлении этой системы матрица M=M₁, где матрица M₁ размерности (m×2) и вектор коэффициентов C₁ размерности (2×1) имеют следующий вид:

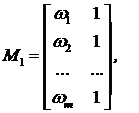
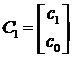(16)

Лабораторная работа № 5

Цель работы:создание программного модуля для формирования индексов риска на основе инструментария универсальной системы MATLAB.

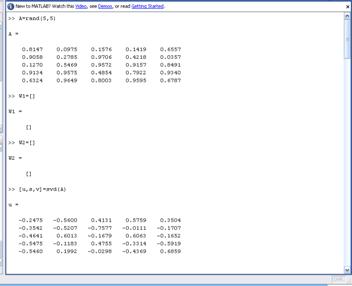
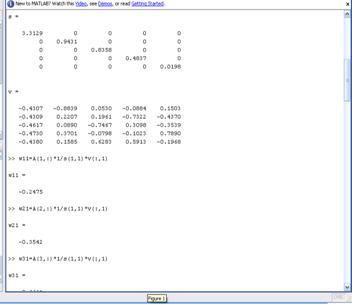
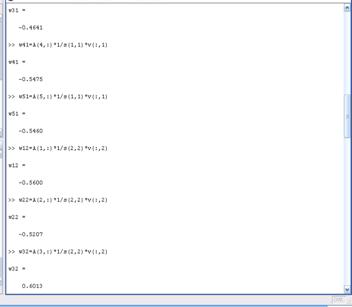
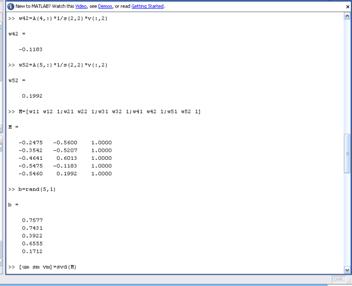
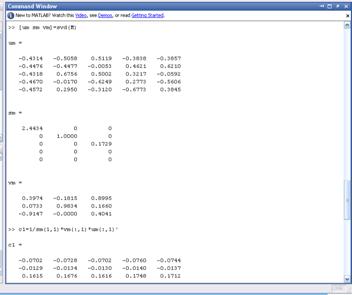
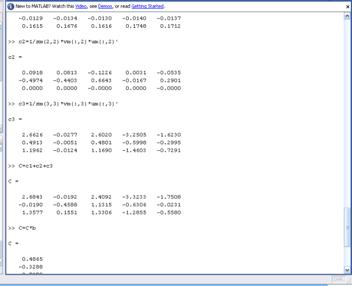
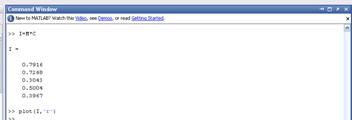
Рисунок 22

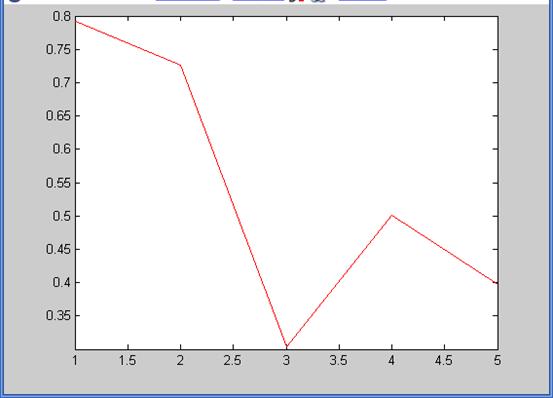
Рисунок 23

Порядок выполнения работы

5.4.2. Порядок оформления отчета

5.4.3. Контрольные вопросы

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.