Формирование количественных ограничений

Рассмотрим несколько вариантов методики определения для дискретного множества исходов:

1) Случай, когда имеются два результата. Методика определения полезности такова:

a) Определяем какой результат более предпочтителен для лица, принимающего решения. Если x₁>x₂, то x₁ предпочтительнее, чем x₂.

b) Определяем вероятность а, при которой достижение результата x₁ будет эквивалентно результату x₂, полученному с вероятностью 1.

c) Оцениваем соотношение между полезностями результатов x₁ и x₂. Для этого примем полезность u(x₂)=1.

Тогда

au(x₁)=u(x₂), u(x₁) =1/a.

2) Случай, когда имеются n возможных результатов x₁,x₂,…,x_n, между которыми установлено отношение предпочтения x₁>x₂>x₃>…>x_n.

Для этого случая методика определения полезности следующая:

а)

a₁u(x₁)=u(x₂).

a₂u(x₂)=u(x₃),

……………….

a_n-1u(x_n-1)=u(x_n).

b) Положив полезность наименее предпочтительного результата x_n равным единице, находим

………………..

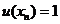
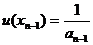
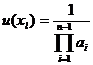
Под формированием количественных ограничений будем понимать определение (вычисление) нескольких точек на кривой, описывающей функцию полезности лица, принимающего решение. Следуя аксиоме 4, выберем x* и х⁰, такие, что х* по крайней мере так же предпочтителен, как любые другие исходы, каждый из которых в свою очередь не менее предпочтителен, чем х⁰. Затем можно произвольным образом назначить конкретные значения полезности двум данным исходам при условии, что u(х*)>и(x⁰). Далее мы хотим получить значение х (назовем его x₁), такое, что исход х₁ равноценен лотерее 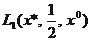с точки зрения лица, принимающего решение. Тогда, поскольку полезности такого исхода и лотереи L₁ должны быть равны, можно записать

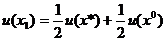. (3.2)

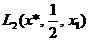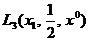Уравнение (3.2) дает третью точку на графике функции полезности (рис. 3.1). Аналогично используя экспертные оценки гарантированных эквивалентов х₂ и x₃ для соответствующих лотерей и , получим значения полезности еще для точек:

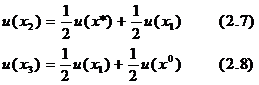
С помощью такого метода всегда можно получить по известным значениям полезности двух исходов значение полезности третьего исхода.

Очень важным является вопрос о том, как найти значение гарантированных эквивалентов. Для получения гарантированного эквивалента требуется процедура взаимодействия исследователя с лицом, принимающим решение (экспертом). Эксперт должен сделать несколько выборов между предлагаемой ему лотереей и предлагаемыми исходами. Например, выбираем исход x_a, испрашиваем эксперта: «Исход x_a предпочтительнее лотереи L₁?» Независимо от ответа нужно знать, как следует изменить значение х (увеличить или уменьшить), чтобы найти искомый гарантированный эквивалент х₁.

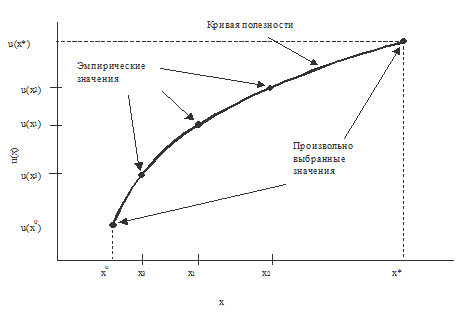Рис. 3.1. Функция полезности

Предположим, что заранее было очевидно, что истинное х₁ должно быть больше, чем x_a. Тогда следовало бы выбрать x_b такое, что x_b>x_a, и спросить эксперта, что предпочтительнее: х_b или L₁? После ответа снова нужно знать, как следует изменить значение х (увеличить или уменьшить). Такой интерактивный процесс (взаимодействие с экспертом) сходится постепенно к исходу х₁, равноценному лотерее L₁, т.е. к гарантированному эквиваленту.

В работе [69] выдвигаются два важных прагматических соображения, которые следует иметь в виду при оценке полезности исходов. Во-первых, исходы, предлагаемые эксперту в качестве вопросов, должны иметь содержательный смысл. Во-вторых, диапазон предлагаемых исходов простых лотерей должен быть до­статочно широк, т. е. необходимо, чтобы исходы отличались друг от друга. Если эти два соображения не учитываются,то ответы лица, принимающего решение, приносят мало пользы для определения предпочтений.

Выбор функции полезности

Предположим, что можно найти некоторое параметрическое семейство функций полезности, которые обладают определенными заранее установленными свойствами. Обозначим такое семейство функций полезности через 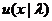, где 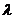— параметры. Тогда выбор соответствующей функции полезности сводится к выбору значений параметров. Это проще и удобнее, чем определять полностью функцию полезности. Кроме того, параметрическое задание функции полезности позволяет провести анализ чувствительности без излишних вычислений. Мы полагаем, что достаточно было бы трех параметров, чтобы описать большинство ситуаций, поскольку тремя или меньшим количеством параметров можно моделировать широкий диапазон характеристик отношения к риску.

Используя параметрическую форму записи и предыдущие оцен­ки отдельных частей кривой полезности [например, (2.6)], можно записать уравнение

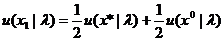,(3.6)

где число неизвестных равно числу параметров. Используя значения гарантированных эквивалентов, полученных экспертным путем, запишем столько уравнений, сколько неизвестных, и раз­решим их относительно параметров, чтобы иметь возможность построить функцию полезности, как показано на рис. 3.1.

Для проверки внутренней совместимости смешанного набора качественных и количественных ограничений, налагаемых на функцию полезности, разработан метод, описанный в [52]. Те же идеи использованы в работе [70], где приводится ряд программ Для выбора функции полезности, которая описывает отношение лица, принимающего решение, к риску и соответствуетего эмпирическим оценкам предпочтений.