Нерекурсивные и рекурсивные фильтры

Согласно разностному уравнению дискретного фильтра (19) очередной выходной отсчет рассчитывается на основе предыдущих выходных отсчетов. Таким образом получается рекурсия и фильтр называется рекурсивным или фильтром с бесконечной импульсной характеристикой (БИХ или в англоязычной литературе IIR infinitе impulse response). Бесконечная импульсная характеристика получается ввиду того, что предыдущее значение на выходе фильтра отлично от нуля, значит текущее значение также будет отлично от нуля (и оно же будет предыдущим для следующего отсчета на выходе), значит и следующий отсчет на выходе будет отличен от нуля. Рассмотрим пример. Пусть имеется БИХ-фильтр первого порядка с передаточной функцией:

(20)

Очевидно, что и . Разностное уравнение данного фильтра имеет вид:

(21)

Рассчитаем импульсную характеристику фильтра. Для этого необходимо подать на вход сигнал . Графически расчет импульсной характеристики представлен на рисунке 4.

Рисунок 4: Импульсная характеристика БИХ фильтра

Видно, что следующий отсчет импульсной характеристики в 2 раза меньше чем предыдущий, и таким образом импульсная характеристика убывает, но никогда не достигает нуля, хотя стремится к нему, т.е. является бесконечной.

Если же все коэффициенты (разумеется кроме коэффициента , который нельзя приравнивать к нулю), то получим фильтр, отсчеты на выходе которого, зависят только от входных отсчетов:

(22)

Такой фильтр называется нерекурсивным или фильтром с конечной импульсной характеристикой (КИХ) или как еще говорят FIR (finite impulse response). Отсчеты импульсной характеристики КИХ фильтра полностью совпадают с коэффициентами и при импульсная характеристика КИХ фильтра равна нулю. Важно также отметить, что передаточная характеристика КИХ фильтра имеет в знаменателе только и не имеет полюсов.

Устойчивость

Во временной области цифровой фильтр устойчив, если его импульсная характеристика удовлетворяет условию (11.18). Теперь определим условия устойчивости цифровых фильтров в -области.

Для этого рассмотрим общую передаточную функцию, заданную выражением (11.40), которое для удобства приведено еще раз:

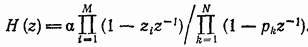
Любой фильтр с передаточными функциями вида (11.163) при называется цифровым фильтром с бесконечной импульсной характеристикой 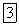поскольку не существует конечного целого числа такого, что

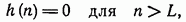
где 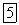— импульсная характеристика фильтра. Для цифровых фильтров положим, что

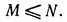
Это предположение верно почти для всех практических случаев. Разложение уравнения (11.163) на простые дроби дает

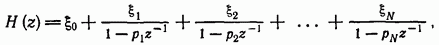
где

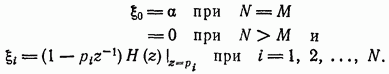
Следовательно, импульсная характеристика, соответствующая выражению (11.163), определяется следующим соотношением:

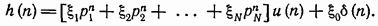
Ясно, что необходимые и достаточные условия того, что импульсная характеристика, заданная выражением (11.167), удовлетворяет критерию устойчивости

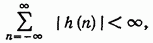
имеют вид .

Это означает, что все полюсы цифрового фильтра расположены внутри единичного круга в z-плоскости.

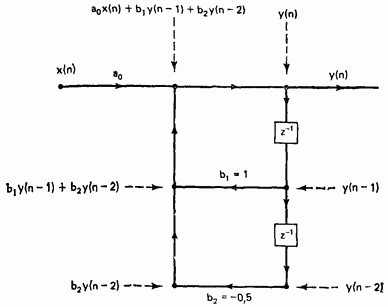
Рис. 11.15. Устойчивая цифровая схема к примеру 11.20.

Пример 11.20. Показать, что схема, приведенная на рис. 11.15, устойчива. Решение. Разностное уравнение, описывающее эту схему, равно

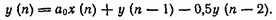
Передаточную функцию схемы можно получить, применив -преобразование к соотношению (11.170):

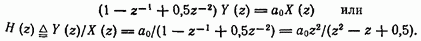
Следовательно, полюсы фильтра расположены в точках

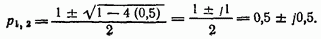
Таким образом, функцию можно переписать в виде

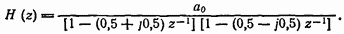
Поскольку

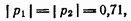
схема на рис. 11.15 устойчива

Если передаточная функция цифрового фильтра представлена в виде

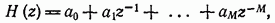
что эквивалентно случаю в выражении (11.163), то цифровой фильтр называют фильтром с конечной импульсной характеристикой (КИХ). Это обозначение используют вследствие того, что импульсная характеристика, соответствующая уравнению (11.175), удовлетворяет следующему условию:

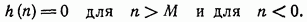
Таким образом, соответствующая импульсная характеристика имеет конечную протяженность. В этом случае отсутствуют полюсы, и поэтому этот тип фильтра всегда устойчив.