II. Перевод дробных десятичных чисел в другие системы счисления.

Алгоритм перевода

1) Умножают десятичную дробь на основание системы счисления, в которую следует перевести эту дробь.

2) В полученном произведении выделяют целую часть. Это будет старший разряд дробной части нового числа.

3) Дробную часть произведения опять умножают на основание новой системы счисления. Целая часть произведения будет следующим разрядом дробной части искомого числа.

4) Пункт 3 повторяют до получения необходимого количества разрядов искомого числа. Если это количество не задано, его следует определить, исходя из условия сохранения точности исходного числа.

Следует отметить, что конечная десятичная дробь после перевода в другие системы счисления не всегда останется конечной. Если в задании не оговорено количество знаков после запятой в новой дроби, его следует определить (см. ниже, на стр. 15).

В качестве примера переведем числа 0,75 и 0,37 из десятичной в двоичную, восьмеричную и шестнадцатеричную системы счисления[5].

a) 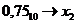[6]

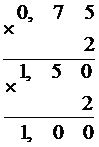
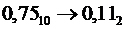
Данная десятичная дробь представляется в двоичной системе счисления конечной дробью.

b) 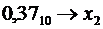[7]

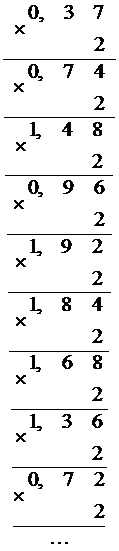
Поскольку данная десятичная дробь не может быть представлена в двоичной системе счисления конечной дробью, определим необходимую точность[8]. В десятичном числе второй знак после запятой даёт точность .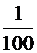

В двоичном числе: первый знак после запятой даёт точность ,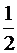

второй – ,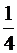

третий – ,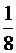

четвёртый – ,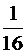

пятый – ,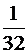

шестой – ,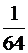

седьмой –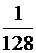

(см. развёрнутую форму записи числа на стр. 6).

Таким образом, чтобы получить точность, не меньшую, чем 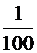, в двоичной дроби следует записать семь знаков после запятой.

Поскольку следующая рассчитанная цифра (результат восьмого умножения) 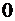, округление производим в меньшую сторону: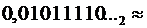

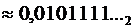
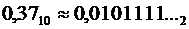
Если бы при последнем умножении получился не ноль, а единица, мы произвели бы округление в большую сторону (единица переходит в старший разряд):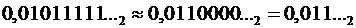

c)

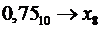
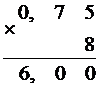
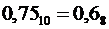
Данная десятичная дробь представляется в восьмеричной системе счисления конечной дробью.

d)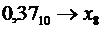

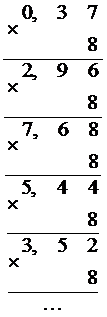
Поскольку данная десятичная дробь не может быть представлена в восьмеричной системе счисления конечной дробью, определим необходимую точность. В десятичном числе второй знак после запятой даёт точность .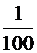

В восьмеричном числе: первый знак после запятой даёт точность ,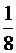

второй – ,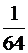

третий –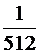

(см. развёрнутую форму записи числа на стр. 6).

Таким образом, чтобы получить точность, не меньшую, чем 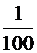, в восьмеричной дроби следует записать три знака после запятой.

Поскольку следующая рассчитанная цифра (результат четвёртого умножения) 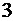, округление производим в меньшую сторону: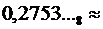

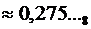
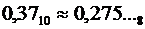
Если бы при последнем умножении получилась не тройка, а четвёрка, мы произвели бы округление в большую сторону (единица переходит в старший разряд):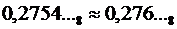

Цифра 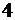в восьмеричной системе счисления является аналогом цифры 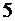в десятичной системе счисления: до неё округление идёт в меньшую сторону, а начиная с неё – в большую.

e) 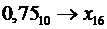[9]

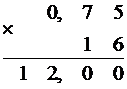
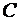
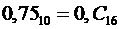
Данная десятичная дробь представляется в шестнадцатеричной системе счисления конечной дробью.

f) 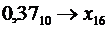[10]

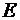
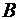
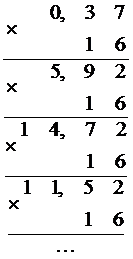
Поскольку данная десятичная дробь не может быть представлена в шестнадцатеричной системе счисления конечной дробью, определим необходимую точность. В десятичном числе второй знак после запятой даёт
точность .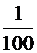

В шестнадцатеричном числе: первый знак после запятой даёт точность ,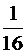

второй –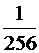

(см. развёрнутую форму записи числа на стр. 6).

Таким образом, чтобы получить точность, не меньшую, чем 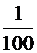, в шестнадцатеричной дроби следует записать два знака после запятой.

Поскольку следующая рассчитанная цифра (результат третьего умножения) 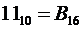, округление производим в большую сторону (единица переходит в старший разряд):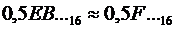

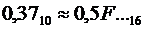
Цифра 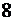в шестнадцатеричной системе счисления является аналогом цифры 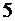в десятичной системе счисления: до неё округление идёт в меньшую сторону, а начиная с неё – в большую.